用跳跃—扩散模型估算市场隐含价值

对于金融专业人士和技术分析师来说，估算一家公司的公允市场价值非常具有挑战性。为了解一家公司的公允价值如何在市场大幅波动时期受到影响，英格兰银行的研究人员对这个问题进行了调研。

公司资产受到利润流和风险敞口等不确定性因素影响。同样，违约风险取决于未来不确定的公司资产价值和对应的偿债义务。通常使用数学模型（如Black Scholes/Merton）来估算公允价值，这些数学模型基于公开但有限的公司信息，如公司的市值、公司债务的面值和无风险利率）。

金融危机暴露了这些方法的缺陷。缺陷之一是这些模型不能将时间序列中相对罕见但极端的运动（或跳跃）考虑进去。我们通常只是偶尔观察到跳跃，但跳跃经常发生在金融危机或其他市场的不确定性时期。例如，图1中的图表显示了2007年上半年英国一家大银行的市值，并显示了多次不同幅度的跳跃（向上和向下）。

评估跳跃对公允价值影响的方法之一，就是使用跳跃扩散模型。这是两个随机过程的组合，其中一个过程是对序列的常规行为进行建模，另一个过程是对随机发生的跳跃进行建模。本文描述的工作流程，运用MATLAB^®、 Statistics and Machine Learning Toolbox™ 以及Signal Processing Toolbox™，基于公开的市场数据，估算企业隐藏市场价值的“跳跃—扩散”模型参数。由此产生的模型可用于推导其他相关数据，如违约概率和利差。

创建“跳跃—扩散”模型

“跳跃—扩散”模型基于标准几何布朗运动(GBM)扩散模型。几何布朗运动模型有两个参数：漂移（平均趋势）和扩散（波动）。这些参数可用来为根据既定价格\(P_{t}\)所得出的连续复合（对数）回报率\(R_{t}\)的分布进行建模：

\[R_t = {\text{log}} \frac{P_{t+∆t}}{P_t} \sim N \Biggl(\left(μ - \frac{σ^2}{2} \right)∆t, σ^2∆t \Biggr), \]

其中\(∆t\) 为时间增量，\(μ\)为漂移参数，\(σ\)为扩散参数。这个模型假设回报率的对数是服从正态分布的，该正态分布的，期望值为 \((μ - {σ^2\over 2}) ∆t\) ，方差为 \(σ^2∆t\)。

我们的“跳跃—扩散”模型在几何布朗运动（GBM）模型的基础上引入了随机跳跃。跳跃\(J_{k}\)是一个 i.i.d.对数正态随机变量序列： \(\text{log} J_{k} \sim N(μ_J,σ_J^2) \)。使用到达率为\(λ\)的泊松过程\(N_{t}\)对跳跃的到达进行建模。回报率可用如下的动态模型表述为：

\[R_t = {\text{log}} \frac{P_t}{P_0} = \left(μ - \frac{σ^2}{2} \right)t + σW_t + \sum_{k=0}^{N_t}\ \text{log}J_k, \]

其中\(W_{t}\)是一个维纳过程。为了对模型进行数值估算，我们将时间t这个连续变量进行离散化，每次跳跃的时间间隔为\([t,t + ∆t]\)。我们假设时间增量\(∆t\)足够小，使得在\([t,t + ∆t]\) 中出现一次以上跳跃的概率可以忽略不计。

与所有复杂的数学模型一样，跳跃扩散模型也在计算上存在一些挑战（例如：实现收敛），需要对优化过程进行仔细分析。利用MATLAB，我们可以用最少的代码来直观地表示方程；估算鲁棒性/稳健性高的模型参数；跟踪优化过程的收敛。

估算模型参数

有五个模型参数需要估算：

• \(μ\) – 几何布朗运动（GBM）的漂移
• \(σ\) – 几何布朗运动（GBM）的扩散
• \(λ\) – 泊松过程中跳跃的到达率
• \(μ_j\) – 跳跃幅度的对数正态位置参数
• \(σ_j\) – 跳跃幅度的对数正态规模参数

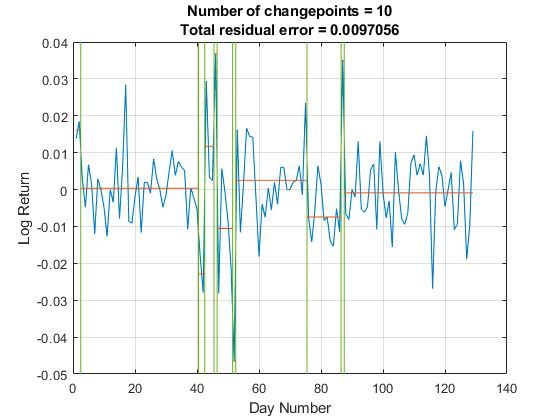
根据可用时间序列数据，我们可以直接估算后三个参数（假定观察到的历史市值能够体现公司真实市场价值的特征）。我们可以使用Signal Processing Toolbox 中的findchangepts 函数自动识别序列中发生突变的点（图2）。在金融时间序列中，当序列的平均值或标准差发生显著变化时，我们可以认为将发生结构变化。在研究金融危机时期或其他高波动时期时，找出标准差变化的点尤为重要。

估算基于Black Scholes/Merton模型，其中\(μ\)是 \(σ\)的函数。为了进行优化，我们使用Statistics and Machine Learning Toolbox 中的mle 函数进行最大似然估算，指定负对数似然函数(negative log-likelihood function)和参数的区间范围作为函数的输入。似然函数的值最终由唯一的未知参数\(σ\)决定。由于市场价值不可观测，因此我们首先用观测到的市值的历史数据对跳跃扩散模型进行拟合，并对市场价值序列生成一个初始估算。我们利用这个初始估算，对这个过程进行反复，直到参数值稳定为止。

在隐含市场价值和债务的模型中，公司的价值分为属于股东的部分和属于债权人的部分。当债务到期时，如果资产足以偿还债务，则除去债务后的剩余价值将归股东所有。否则股东一无所获。

债务价值相当于持有的无风险债务加上卖出对资产价值的看跌期权：如果资产足以清偿债务，那么债权人将获得足额的偿还。如果资产不足以清偿债务，那么债权人将获得全部资产。债务不能全部得到清偿的情况被视为风险。债权人以高于无风险利率的信贷利差作为持有风险债务的回报，该利差可以看作是看跌式期权的价值。

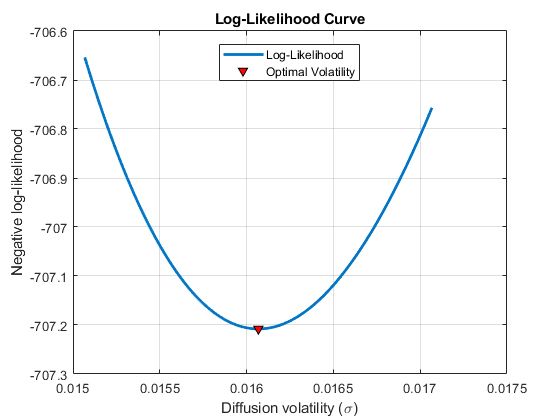
资产价值满足一个包括公司市值和风险债务价值的隐式方程，而风险债务的价值又是资产价值和其他变量（如无风险利率）的函数。在最大似然估计过程中，我们使用MATLAB中的fzero 函数来求解资产价值的隐式方程。收敛后，我们在可能的解点的邻域中绘制负对数似然函数，来验证局部最小点是由mle函数确定的（图3）。

推算市场价值

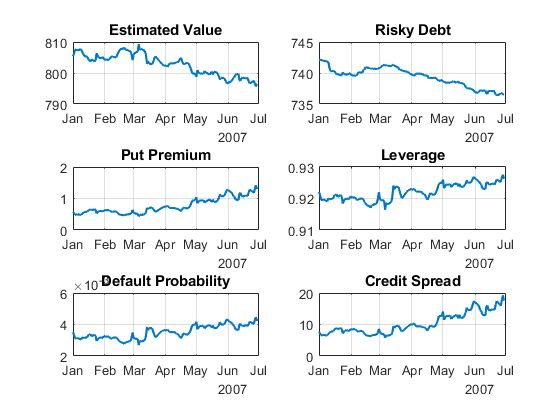
在拟合模型之后，我们可以用它来推算资产的市场价值和相关数据，如资产的隐含看跌期权价值和资产的杠杆率。图4所示的就是这些数据的时间序列。不出所料，我们看到，公司的市值和推算出的公允价值下降时，看跌期权的价值迅速增加。杠杆率作为衡量市场价值与债务比率的指标，也随着资产价值的下跌而增加。

在开发并实现一个跳跃扩散模型参数的估算过程之后，我们使用MATLAB Live Editor  将结果作为实时脚本与同事共享。以上流程可以应用于不同类别资产的各种时间序列数据。由于许多金融数据在金融危机时期和市场高度不确定时期都会出现跳跃，因此本模型的潜在应用范围很广。