GPU让我尽情享受对分形学的痴迷

我是个分形迷。现在，我有了一个让我上瘾的GPU。GPU的设计初衷是图形加速，但MATLAB^®用它们来加速计算。分形学¹是需要大量计算的图形学，可以与GPU实现完美结合。

GPU重新激起了我对曼德尔勃特集合本身的兴趣，并通过三种分形变体简化了我的工作，这三种变体包括：“燃烧之船”、“权力之塔”和牛顿法的全局收敛行为。

我的GPU是NVIDIA^®Titan V，安置在一个比笔记本电脑更大的独立外壳中，并提供独立电源和散热装置。计算这些分形的速度大约是CPU的300倍，完全改变了我与mandelbrot程序的交互方式。我在程序中引入了gpuArray，现在可以使用与屏幕分辨率相当的网格分辨率，并不断迭代，直到图像中的细节变得清晰可见。

曼德尔勃特集合解密

曼德尔勃特现象一直存在。曼德尔勃特涉及到复数的简单迭代，从初始点\(z_0\)开始。曼德尔勃特集合是由\(z_0\)值组成的复平面上的区域，其中由以下公式定义的轨迹保持有界：

\[z_{k+1} = z_{k}^2 + z_{0}, k=1, 2, ...\]

这就是整个定义。如此简单的定义竟能产生如此迷人的复杂性，真是令人惊讶。

上面所示的彩色图像是一个曼德尔勃特集合的鸟瞰视图。它没有办法显示集合边界外缘详细的结构。事实上，曼德尔勃特集合有小的细丝达到边缘地区，但在此视图中很难看到边缘。

图1是曼德尔勃特集合几何图形的略图。最大的组成部分是一个心形的心脏曲线，由以下参数方程的曲线包围

\[z = e^{it}/2 - e^{2it}/4, -\pi \le t \le \pi \]

心脏线的左边是一个半径为¼的圆盘。心脏线和圆盘的连接部位在红点处。稍后再详细介绍那个红点。

在这两个部件的周围是无穷多的近似圆形的圆盘，圆盘的直径逐渐递减。最小圆盘的精确位置和形状只能通过计算来确定。

最近已经证明，曼德尔勃特集合是数学上连接的，但连接区域有时太薄，我们无法在图形屏幕上解析它，甚至无法在合理的时间内计算它。

计算曼德尔勃特集合

我们联想到的曼德尔勃特的迷人图案来自集合外的边缘区域。

这是计算的核心函数。输入是一个复标量起点z0和一个实标量参数，我称之为depth。输出是一个计数kz。如果因为z在半径为2的圆盘之外而终止迭代，则z注定会变成无穷大，而计数kz可以用作色图的索引。另一方面，如果z在depth迭代中幸存，则声明它在曼德尔勃特集合中。

function kz = mandelbrot(z0,depth)
    z = z0;
    kz = 0;
    while (z*conj(z) <= 4) & (kz <= depth)
        kz = kz + 1;
        z = z*z + z0;
    end
end

让我们在复平面上生成一个点网格，覆盖宽度为w的平方，以复点zc为中心。

grid = 512;
s = w*(-1:1/grid:1);
[u,v] = meshgrid(s+real(zc),s+imag(zc));

现在要介绍的是，在CPU上运行的程序和在GPU上运行的程序之间的唯一区别。要在CPU上生成网格，

z0 = u + i*v;

对于GPU，

z0 = gpuArray(u + i*v);

然后，对于任一处理器，以下语句

kz = arrayfun(@mandelbrot,z0);

将标量函数mandelbrot应用于数组z0的所有元素。在CPU上，这是一个向量化网格上的双重for循环。在GPU上，语句被分解成数百个并行运行的独立任务。

现在，让我们来看看来自曼德尔勃特边缘的两幅不同寻常的图像。

在边缘上

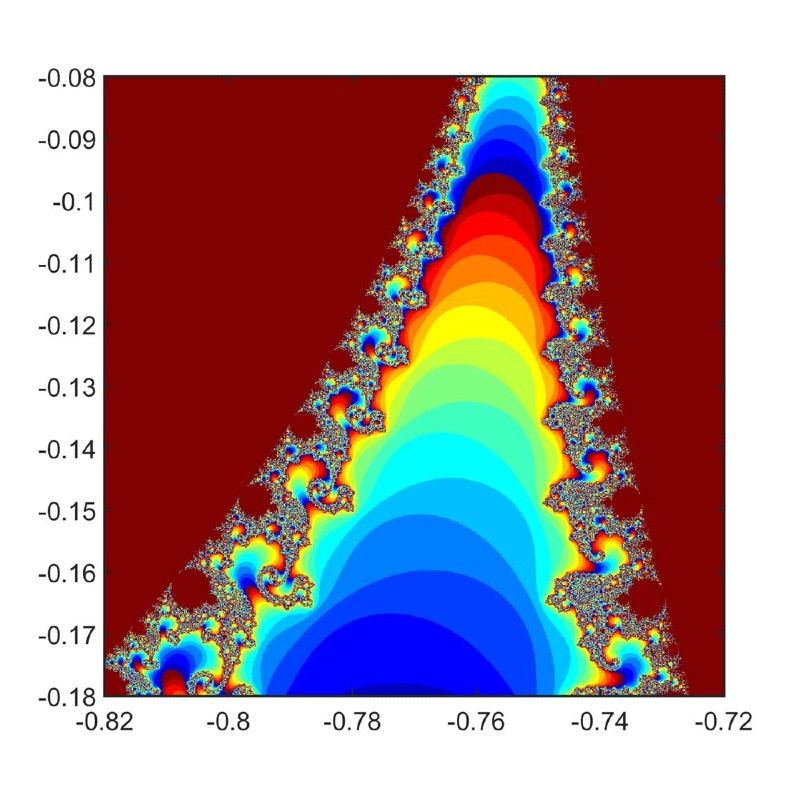
被称为海马谷的区域位于中央心脏线和它左边的圆盘之间。实际上有两个山谷，一个在实轴上，一个在实轴下。它们在图1中看到的红点处交汇。发挥点想象力，您就可以想象出生活在图2中的小海洋生物。稍后我们将看到，山谷也包含隐伏的π。

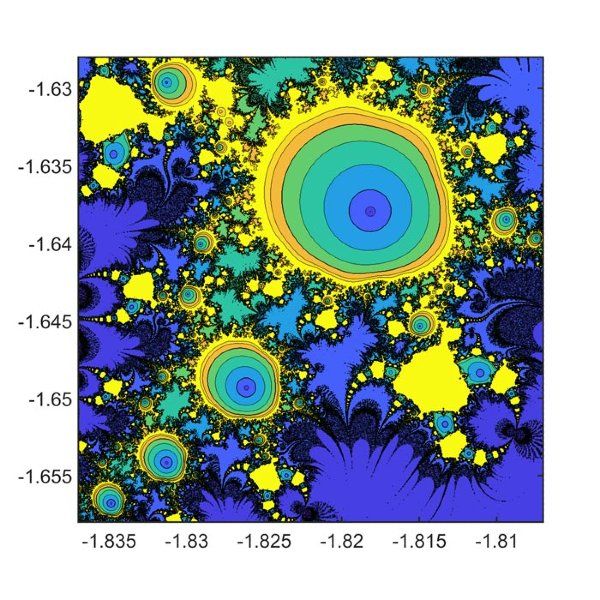
由于曼德尔勃特集合是自相似的，所以它包含无限多个微型曼德尔勃特，每个曼德尔勃特的形状都与大的曼德尔勃特相同。如图3所示，其放大倍数为10¹⁰。

隐伏的π

1991年，科罗拉多州立大学的Dave Boll发现了一个惊人的结果。Boll当时正在研究曼德尔勃特迭代在海马谷中的行为。山谷接近轴时会变得更窄，它们在图1中的红点处(-3/4,0)交汇。

我们可以在一个以-3/4 + yi为中心、刚刚偏离轴的小网格上重复Boll的计算，y代表一个极小的值，i代表虚数单位。

y = 1.0e-07
zc = -3/4 + y*i

使网格足够大，刚好可以接触到轴。

width = 2*y
grid = 4

选择depth使其与y成反比，这会使它变得非常大。

depth = 4/y

使用这些参数，运行上面的代码。它会生成

kz =

40000000    40000000    40000000    40000000    40000000
40000000    40000000    40000000    40000000    40000000
40000000    40000000    31415926    40000000    40000000
40000000    40000000    20943951    40000000    40000000
40000000    40000000    15707963    40000000    40000000

这不是侥幸。Aaron Klebanof于2001年发表的一篇论文《曼德尔勃特集合中的π》分析了心脏线前端尖点的类似计算。

接下来，我们要介绍的是曼德尔勃特迭代的一个奇怪变体。

燃烧之船

燃烧之船来自一个奇怪的迭代：

\[z_{k+1} = F(z_k) + z_{0}, k=1, 2, ...\]

其中

\[F(z) = (|Re(z)| + i |Im(z)|)^2\]

我说这很奇怪，是因为函数\(F(z\)不是解析的。我对这个迭代很感兴趣，因为在以下图片中有不可思议的相似之处。

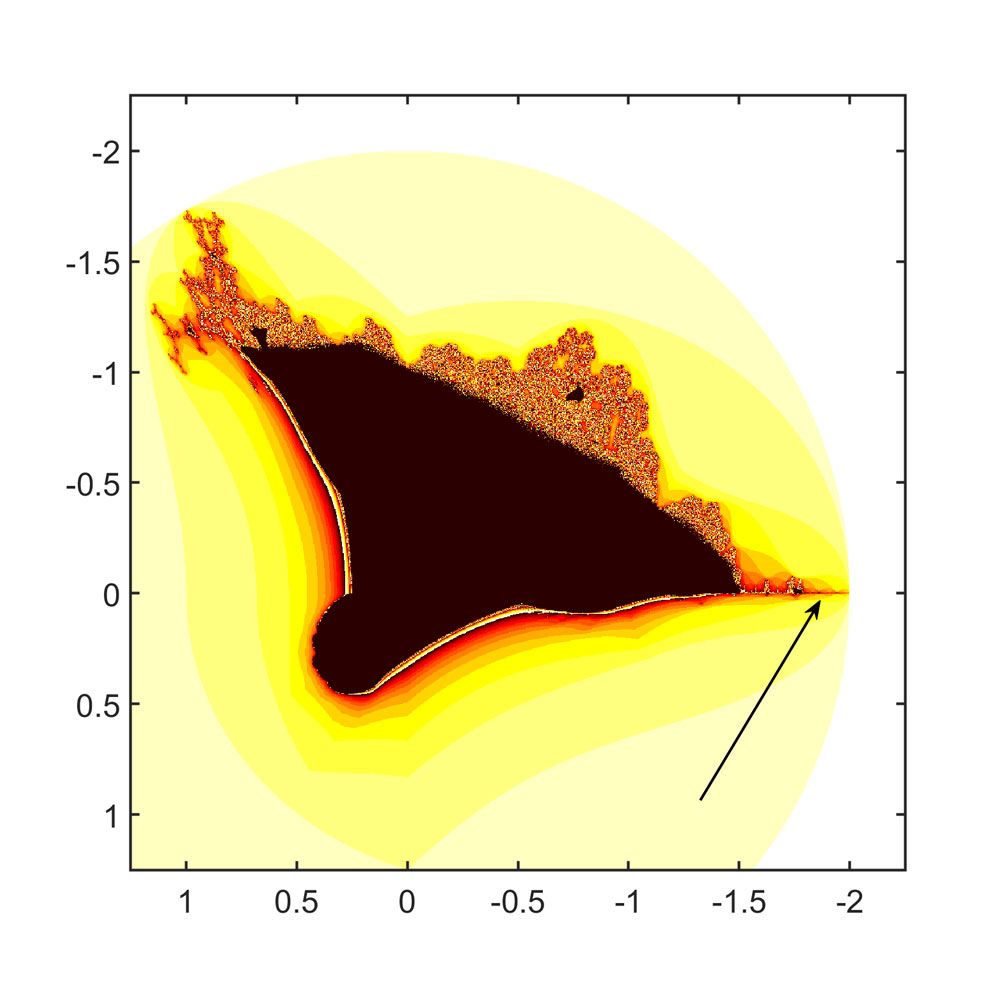
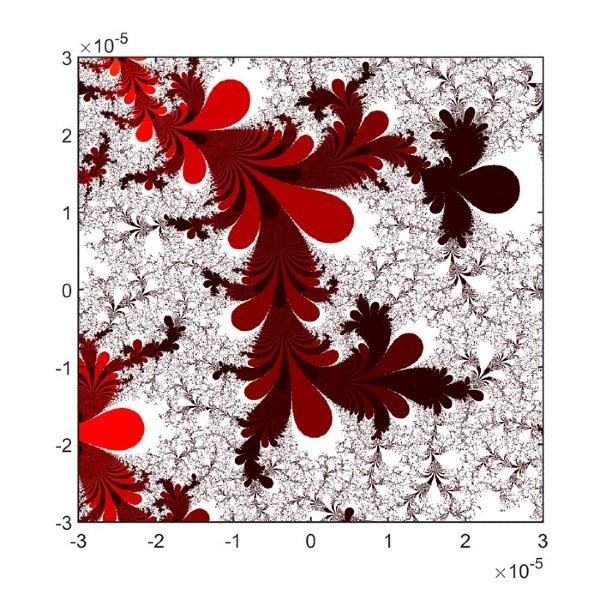
如图4所示，初始域是一个以-0.5-0.5i为中心的宽度为3.5的正方形。我在船的尾迹处插入了一个指向相关区域的箭头。

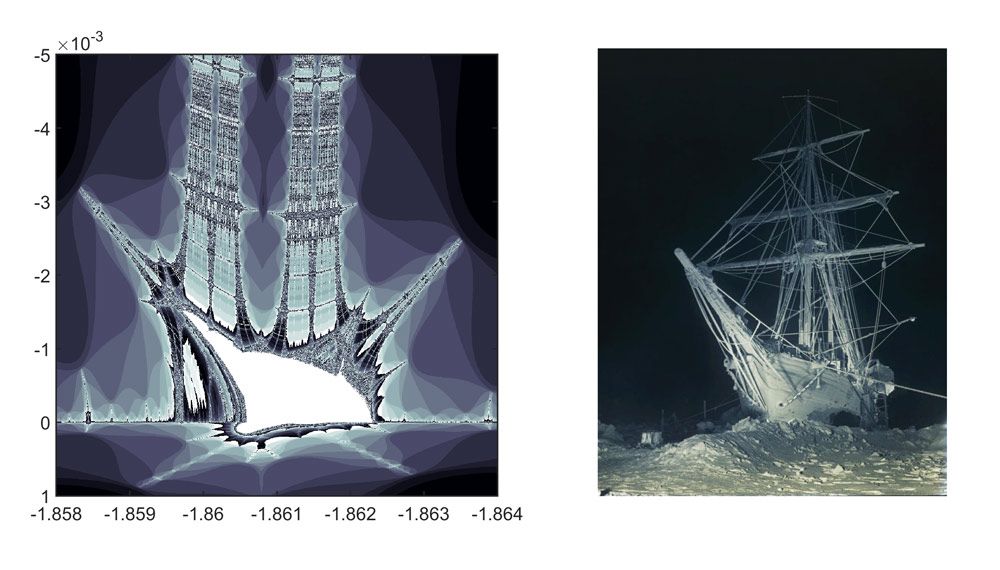
将船的尾迹放大500倍至-1.861-.002i。使用bone色图使它看起来是冷的而不是燃烧的。图5显示了分形的结果，旁边是1915年南极探险家欧内斯特·沙克尔顿的船“耐力”号在威德尔海冻结的照片。

权利之塔

从任意复数\(z\)开始，反复取幂。

\[z, z^z, z^{z^z}, . . .\]

我们可以将其表示为迭代。从 \(y_0 = 1\) 开始，令

\[y_{k+1} = z^{y_k}\]

如果\(z\)太大，则此迭代将膨胀到无穷大。对于某些\(z\)，它会收敛到一个有限的极值。例如，如果\(z = \sqrt 2\)，\(y_k\)将收敛于2。最有趣的情况是\(y_k\)接近一个循环。例如，如果\(z\)接近2.5+4\(i\)，则循环长度为7。

 2.4684 + 4.0754i
-0.6216 + 0.3634i
 0.2603 - 0.0184i
 1.4868 + 0.3613i
-3.4877 + 6.1054i
 7.7632e-06 - 2.6617e-06i
 1.0000 + 0.0000i
 2.4684 + 4.0755i

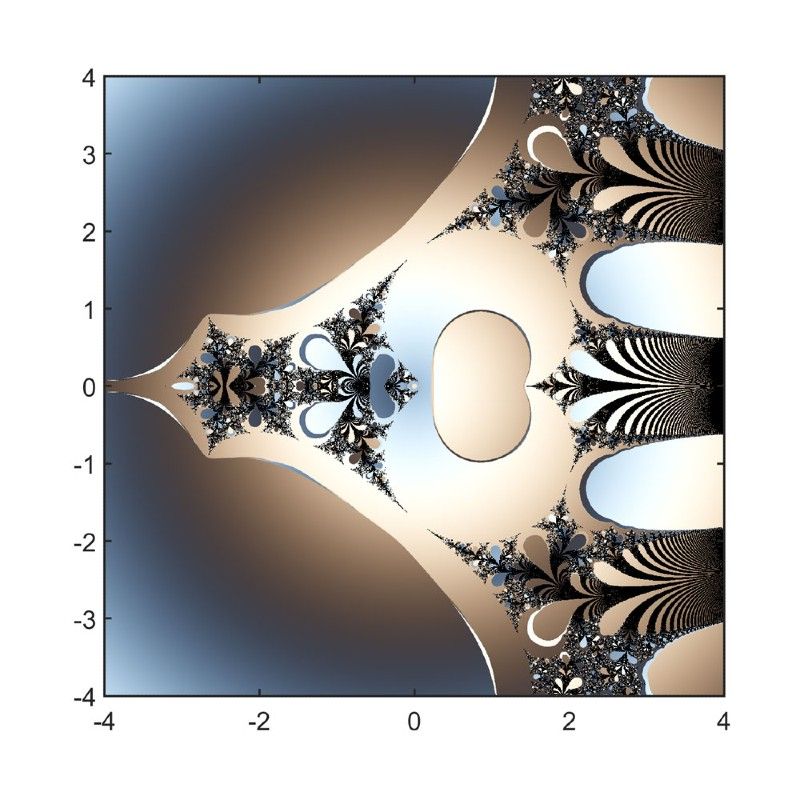
这个循环长度是“权力之塔”分形的基础。图6显示了整体的分形。

放大10⁵倍并更改色图将生成图7所示的图像。

牛顿法

当牛顿法的起始点不接近函数的零点时，全局行为会显得不可预测。从复杂平面上一个起始点区域到收敛点的迭代计数的等高线图生成了令人深思的分形图像。

迭代是常见的。选择一个函数 \(f(z)\) 对 \(f '(z)\)求导。从 \(z_0\) 开始，令

\[z_{k+1} = z_{k} – f(z_{k})/f '(z_{k})\]

它最终会收敛到f的零点。计算接近目标所需的迭代次数。

有许多函数（和色图）可供选择。我最喜欢的三次多项式是

\[f(z) = z^3 – 2z – 5\]

图8显示了被划分为三个区域的复杂平面，其中迭代收敛于立方的三个零中的一个。这些区域之间是强烈的分形作用区域，如图中黑色部分所示。

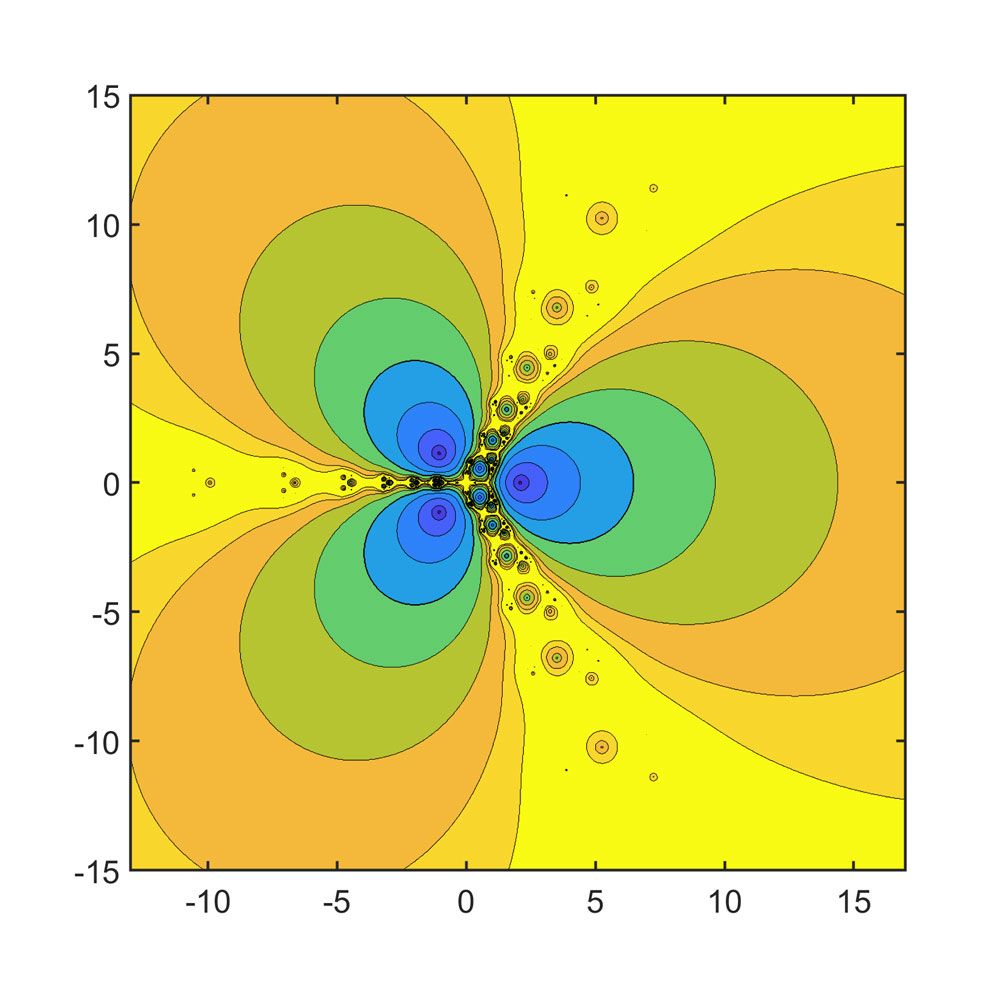
图9显示了寻找以下函数式零点的牛顿法的全局行为

\[f(z) = tan(sin(z)) - sin(tan(z))\]

该函数有无穷多个零和一个无界的一阶导数。

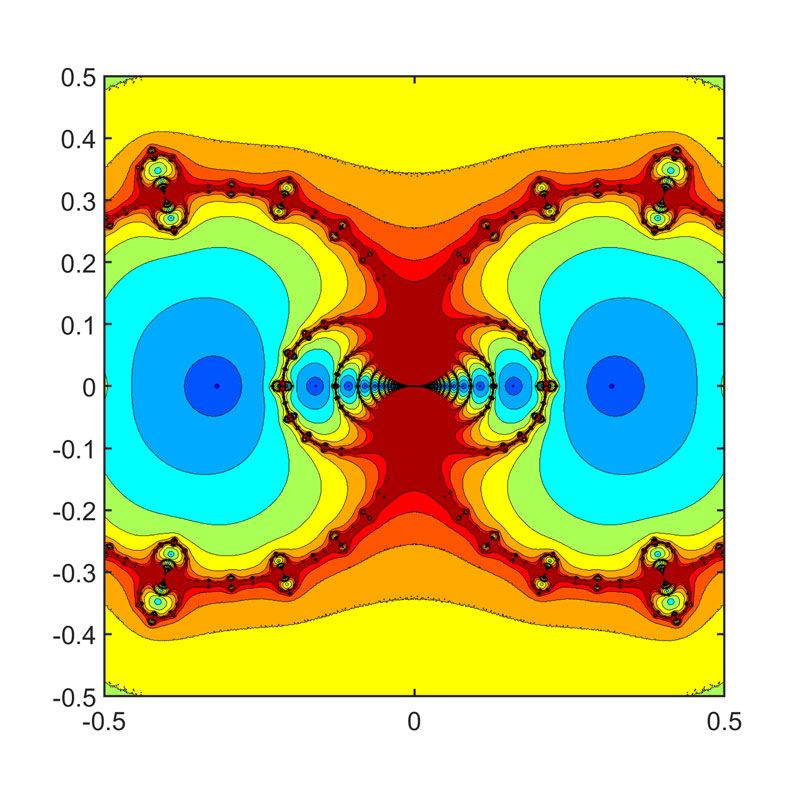
图10的函数是

\[f(z) = z\;sin(1/z) \]

最突出的蓝色区域环绕在±1/π的零处。

本文所示的许多图像对我来说是全新的——我以前从未见过它们。利用GPU进行计算，使它们得以展示在公众面前。

¹ 分形这个术语是由Benoit Mandelbrot (1924-2010)提出的，他是一位波兰/法国/美国的数学家，职业生涯的大部分时间都在位于纽约约克敦海茨的IBM华生研究中心度过。