University of Geneva Develops Advanced Portfolio Optimization Techniques
"For years I have said that people who use Microsoft® Excel® or C to do advanced financial analysis are wasting their time. For any kind of numerical computation, I can’t see using anything other than MATLAB."
Challenge
Develop and implement a general-purpose, data-driven heuristic for portfolio optimization
Solution
Results
- Solutions found in minutes
- Efficiency improved through visualization
- Students gain practical experience
When Harry Markowitz developed a mean-variance framework for modern portfolio optimization more than 50 years ago, simplicity was a key part of its appeal. However, the adoption of more sophisticated risk measures—for example, value at risk—and constraints, including restrictions on the maximum number of different assets in a portfolio and minimum holding size, has made it all but impossible to optimize portfolios with classical techniques.
Using MATLAB®, Parallel Computing Toolbox™, and MATLAB Parallel Server™, researchers at the University of Geneva have developed a multipurpose, data-driven optimization heuristic that addresses the challenges of more sophisticated risk measures and practical portfolio constraints.
"Financial analysts have been talking about downside risk for years, but few have attempted to use it for portfolio selection because the resultant optimization problem is difficult to solve," says Professor Manfred Gilli of the Department of Econometrics at the University of Geneva. "Using heuristic methods and MathWorks tools, we have developed a system that any analyst can use to arrive at optimal solutions very quickly."
Challenge
Gilli and his colleagues sought to develop an automated system for portfolio selection using heuristics to solve complex optimization problems. Heuristic algorithms use trial-and-error methods to find solutions for mathematically complex problems. Although economists are familiar with implementing heuristic techniques, such as threshold accepting, finding a set of parameters to make algorithms work effectively is challenging.
“A financial analyst without sufficient experience with heuristic methods can waste lots of time trying to determine parameters such as the threshold sequence without a powerful analytics tool,” says Gilli, who wanted to automatically determine effective parameters for the algorithms based on the specified constraints and financial data.
As a teaching professor, Gilli also needed tools that would help students understand the concepts used in his research.
Solution
Gilli and his colleagues used MATLAB, Parallel Computing Toolbox, and MATLAB Parallel Server to develop and implement a threshold accepting algorithm that rapidly solves complex portfolio optimization problems involving advanced risk functions and constraints.
The group started by implementing a threshold accepting heuristic in MATLAB.
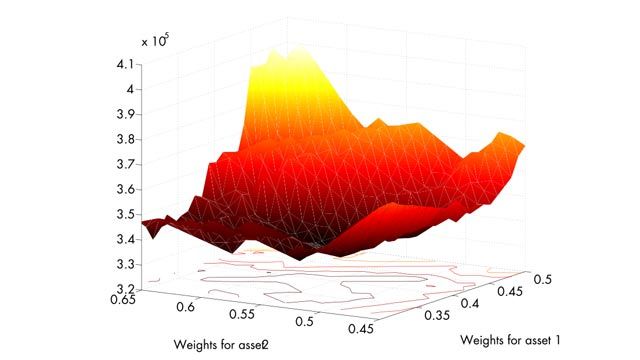
As they developed the algorithm to implement this heuristic, they relied on MATLAB graphs and plots to visualize intermediate results and understand how the algorithm was working with various data sets.
Gilli then used MATLAB to develop an application that automatically determines an effective threshold sequence based on the constraints specified and the data analyzed for a particular problem before running the optimization algorithm.
The application runs dozens of times with different starting points to find the global minimum of an optimization problem with many local minima.
A single execution of the application using this real-world data required from three to seven minutes to complete. Needing dozens of results to arrive at a solution, Gilli used MathWorks distributed computing tools to create distributed applications that execute on a computing cluster. Using the MathWorks job manager as a scheduler, Gilli executed 32 independent tasks on 32 processors in the same time required to execute the algorithm once on a single processor.
To benchmark and validate the approach, the group solved the classical Markowitz model with the heuristic. Gilli then used Optimization Toolbox™ and Financial Toolbox™ to solve the Markowitz model with a classical approach, and compared the results with the heuristic solution.
Gilli’s students use MATLAB, Optimization Toolbox, Statistics and Machine Learning Toolbox™, and Financial Toolbox to implement classical portfolio techniques and more advanced heuristic methods. He is now using the algorithm to determine the most appropriate risk measures for various market conditions.
Results
Solutions found in minutes. “We frequently need to run the algorithm with 100 or more different starting points,” says Gilli. “At three to seven minutes per run, a single solution could require 11 hours or more. With Parallel Computing Toolbox, we can complete 32 runs independently on our 32 different processors, and get a solution in minutes. Parallel Computing Toolbox is perfect for this kind of problem, and it is completely scalable.”
Efficiency improved through visualization. “Working in MATLAB is faster and gives us a complete set of tools,” says Gilli. “In particular, the visualization capabilities of MATLAB enabled me to see intermediate results and understand what the algorithms were doing so I could make improvements.”
Students gain practical experience. Gilli uses MathWorks tools to teach the same concepts that he applies in his research. “My students solve heuristic optimization problems for their exams,” says Gilli. “With MATLAB, students can code their own algorithms, see how things work at a low level, and later use the existing routines from various toolboxes. I wouldn’t use anything else.”