Main Content

Reconstruct Channel Impulse Response Using CDL Channel Path Filters

Open Live Script

Reconstruct the channel impulse response and perform timing offset estimation using path filters of a Clustered Delay Line (CDL) channel model with delay profile CDL-D from TR 38.901 Section 7.7.1.

Define the channel configuration structure using an nrCDLChannel System object. Use delay profile CDL-D, a delay spread of 10 ns, and UE velocity of 15 km/h:

v = 15.0;                    % UE velocity in km/h
fc = 4e9;                    % carrier frequency in Hz
c = physconst('lightspeed'); % speed of light in m/s
fd = (v*1000/3600)/c*fc;     % UE max Doppler frequency in Hz
 
cdl = nrCDLChannel;
cdl.DelayProfile = 'CDL-D';
cdl.DelaySpread = 10e-9;
cdl.CarrierFrequency = fc;
cdl.MaximumDopplerShift = fd;

Configure the transmit array as [M N P Mg Ng] = [2 2 2 1 1], representing 1 panel (Mg=1, Ng=1) with a 2-by-2 antenna array (M=2, N=2) and P=2 polarization angles. Configure the receive antenna array as [M N P Mg Ng] = [1 1 2 1 1], representing a single pair of cross-polarized co-located antennas.

cdl.TransmitAntennaArray.Size = [2 2 2 1 1];
cdl.ReceiveAntennaArray.Size = [1 1 2 1 1];

Create a random waveform of 1 subframe duration with 8 antennas.

SR = 15.36e6;
T = SR * 1e-3;
cdl.SampleRate = SR;
cdlinfo = info(cdl);
Nt = cdlinfo.NumTransmitAntennas;
 
txWaveform = complex(randn(T,Nt),randn(T,Nt));

Transmit the input waveform through the channel.

[rxWaveform,pathGains] = cdl(txWaveform);

Obtain the path filters used in channel filtering.

pathFilters = getPathFilters(cdl);

Perform timing offset estimation using nrPerfectTimingEstimate.

[offset,mag] = nrPerfectTimingEstimate(pathGains,pathFilters);

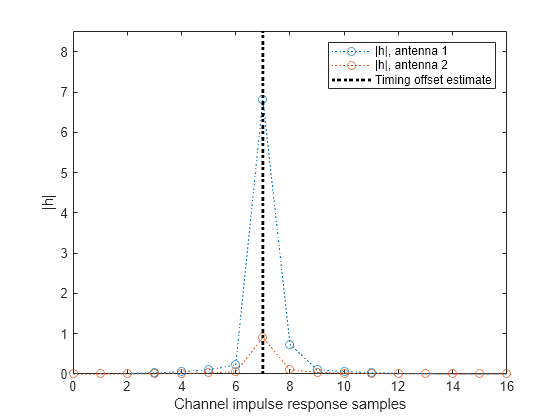
Plot the magnitude of the channel impulse response.

[Nh,Nr] = size(mag);
plot(0:(Nh-1),mag,'o:');
hold on;
plot([offset offset],[0 max(mag(:))*1.25],'k:','LineWidth',2);
axis([0 Nh-1 0 max(mag(:))*1.25]);
legends = "|h|, antenna " + num2cell(1:Nr);
legend([legends "Timing offset estimate"]);
ylabel('|h|');
xlabel('Channel impulse response samples');

Figure contains an axes object. The axes object with xlabel Channel impulse response samples, ylabel |h| contains 3 objects of type line. These objects represent |h|, antenna 1, |h|, antenna 2, Timing offset estimate.

See Also

Functions