Gravity Models with Precessing Reference Frame
This example shows how to implement various gravity models with precessing reference frames using Aerospace Blockset™ blocks. Precession is a change in the orientation of the rotational axis of a rotating body. The orientation of the rotational axis of Earth determines the angular velocity experienced at different positions, which in turn affects the computed centrifugal forces. The Aerospace Blockset blocks are shown in red.
Open the Example Model
The example asbGravWPrec.slx is configured to simulate a reference trajectory that is 330 km over the Earth with a ground track along the prime meridian and a period of 10 seconds.
open_system('asbGravWPrec.slx');
Summary
This example shows how to compute gravity forces using these gravity model blocks: WGS84, spherical harmonic, and zonal harmonic gravity model.
Since spherical and zonal harmonic models require positions in the Earth-Centered Earth-Fixed (ECEF) frame, the example needs to perform a coordinate change from geodetic latitude and longitude to ECEF coordinates.
Zonal and spherical harmonic gravity models also do not include centrifugal effects, so centrifugal forces needs to be computed separately and summed with the respective gravity models.
To account for Earth precession and the influence it has on rotation rate, the centrifugal effect model block uses a specific rotation rate from a given Julian date to compute the centrifugal forces. The inclusion of the effects Julian date has on centrifugal forces is useful in long simulations where the effects of Earth's precession cannot be neglected.
This example does not take into account coriolis acceleration.
The WGS84 gravity model outputs gravity components in the North-East Down (NED) frame. To compare gravity models, the example computes a Direction Cosine Matrix (DCM) to convert the results into the ECEF frame to be consistent with the computed gravity values from the other two models.
Determine Earth-Centered Earth-Fixed (ECEF) Position
To use the zonal harmonic and spherical harmonic gravity models, you need positions in the ECEF reference frame. Use the LLA to ECEF Position block to determine ECEF positions from geodetic latitude, longitude, and altitude.

Compute Zonal Harmonic Gravity for Earth
Use the Zonal Harmonic Gravity Model block to calculate the gravity components up to the fourth order in the ECEF coordinate system in meters per second squared.
Since the block does not include centrifugal effects of planetary rotation and the effects of a precessing reference frame, use the Centrifugal Effect Model Block to compute the gravity components due to centrifugal effects.

To include the effects of precession, select the Input planetary rotational rate check box.

Selecting this check box creates an additional input port to the block to specify a rotational rate. The changes that the Earth precession has on its rotational rate can be accurately approximated as a function of Julian date through the equations in the subsystem Rotational Rate in a Precessing Reference Frame.
Compute Spherical Harmonic Gravity for Earth
To compute the gravity components in the ECEF coordinate system in meters per second squared, use the Spherical Harmonic Gravity Model block with the default EGM2008 central body model selected and a default degree of 120. This block does not include centrifugal effects of planetary rotation. To get total gravity potentials, add the gravity components of the centrifugal effects to the computed values.

Calculate WGS84 Gravity for Earth
Use the WGS84 Gravity Model to calculate zonal harmonic gravity components in the NED coordinate system in meters per second squared. By default, the WGS84 Exact gravity model does not include centrifugal effects. To include centrifugal effects, clear the No centrifugal effects check box.
To compare the gravity models, their outputs must be in the same coordinate system. You can transform WGS84 gravity from NED coordinates to ECEF Coordinates by multiplying NED coordinates with a direction cosine matrix (DCM). This matrix is a 3-by-3 transformation matrix that converts values between two coordinate frames. Use a Direction Cosine Matrix ECEF to NED block to generate the DCM. This block accepts an input latitude and longitude and returns the DCM required to convert coordinates in the ECEF coordinate frame to the NED coordinate frame.

Since the resultant DCM is for a conversion from the ECEF to NED coordinate frame, take the transpose of the resultant matrix using the transpose block to generate the NED to ECEF DCM.
Comparison Plots for Different Gravity Models with Centrifugal Effects
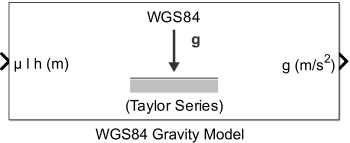
Simulate the model and observe the latitude (in yellow) and longitude (in blue) position history of the trajectory.
sim('asbGravWPrec.slx');
Figure 1: Latitude and longitude position history
This figure shows the time history gravity components each gravity model computes. Observe that when computing gravity at various points along a trajectory, the results between the models are similar. While the differences are relatively small, it is important to note that the simulation trajectory is in an open loop system (the trajectory is not computed using gravity), and if considered in a closed loop system, the impact will become more significant over time.

Figure 2: Gravity components in the Earth-Centered Earth-Fixed coordinate frame
See Also
WGS84 Gravity Model | Spherical Harmonic Gravity Model | Centrifugal Effect Model | Zonal Harmonic Gravity Model