Model a Lunar Free-Return Trajectory in Satellite Scenario Using Numerical Orbit Propagation
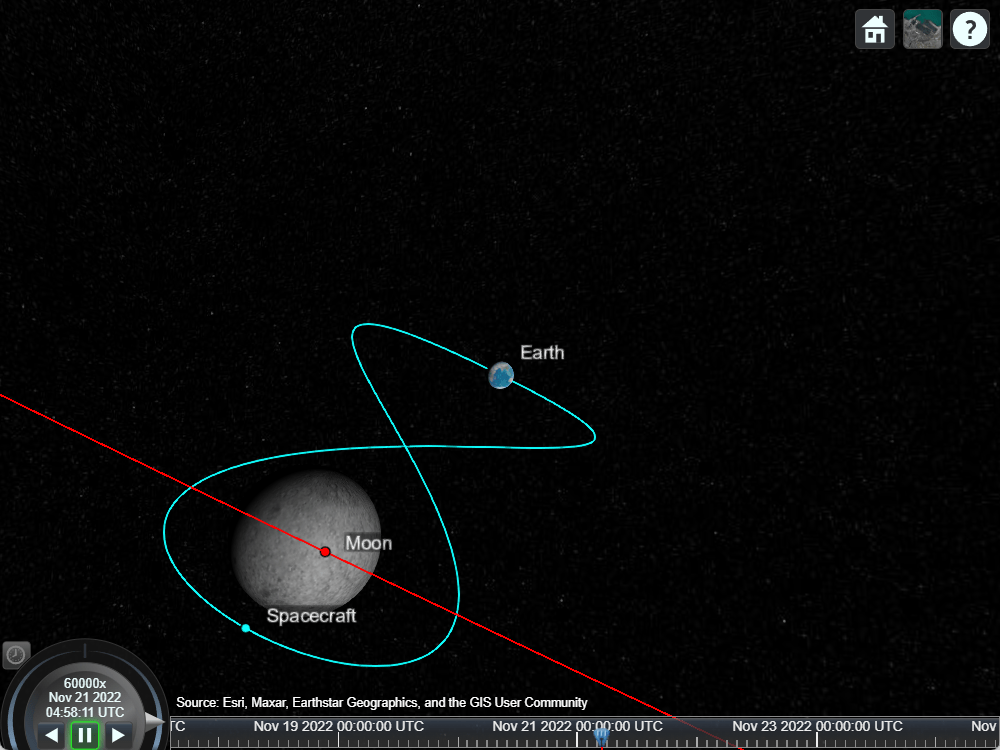
This example simulates a lunar free-return trajectory using satelliteScenario. The lunar free-return trajectory in consideration is a circumlunar trajectory that first takes a spacecraft from Earth to the Moon. The spacecraft then performs a gravity assist around the far side of the Moon and returns back to Earth. The free-return trajectory involves no intermediate maneuvers after the initial translunar injection burn. The translunar injection burn is a maneuver that is performed while in an Earth parking orbit to place the spacecraft on the free-return trajectory. The advantage of such a trajectory is that the spacecraft is guaranteed to return back to Earth even if its propulsion system fails. This is crucial for human lunar missions to avoid the possibility of getting stranded in cislunar space and also possibly escaping the Earth-Moon system and entering into a heliocentric orbit.
In this example, the gravitational potential model of the Earth is set to point-mass. The third body gravity from all supported solar system objects is accounted for. The scenario begins right after the translunar injection burn. The scenario ends when the spacecraft returns to Earth and reaches periapsis at an altitude of 60 km.
Create Satellite Scenario
Create a satelliteScenario object. Set StartTime to November 17, 2022, 2:40:00 PM UTC, StopTime to November 24, 2022, 12:45:00 PM UTC, and SampleTime to 60 seconds.
startTime = datetime(2022,11,17,14,40,0);
stopTime = datetime(2022,11,24,12,45,0);
sampleTime = 60; % s
sc = satelliteScenario(startTime,stopTime,sampleTime)sc =
satelliteScenario with properties:
StartTime: 17-Nov-2022 14:40:00
StopTime: 24-Nov-2022 12:45:00
SampleTime: 60
AutoSimulate: 1
Satellites: [1×0 matlabshared.satellitescenario.Satellite]
GroundStations: [1×0 matlabshared.satellitescenario.GroundStation]
Platforms: [1×0 matlabshared.satellitescenario.Platform]
Viewers: [0×0 matlabshared.satellitescenario.Viewer]
AutoShow: 1
Add Numerical Propagator
Add a numerical orbit propagator to the scenario. Configure the ordinary differential equation (ODE) solver options, gravitational potential model and the third body gravity. Include third body gravity from all supported solar system bodies. Note that the numerical propagator also supports inclusion of perturbations due to drag from Earth atmosphere and solar radiation pressure. However these effects are ignored in this example.
numericalPropagator(sc, ... ODESet=odeset(RelTol=1e-8,AbsTol=1e-8,MaxStep=300), ... IncludeThirdBodyGravity=true, ... ThirdBodyGravitySource=["Sun" "Mercury" "Venus" "Moon" "Mars" "Jupiter" "Saturn" "Uranus" "Neptune" "Pluto"], ... GravitationalPotentialModel="point-mass")
ans =
NumericalPropagatorOptions with properties:
ODESolver: "ode45"
ODESet: [1×1 struct]
GravitationalPotentialModel: "point-mass"
IncludeAtmosDrag: 0
IncludeThirdBodyGravity: 1
ThirdBodyGravitySource: ["Sun" "Mercury" "Venus" "Moon" "Mars" "Jupiter" "Saturn" "Uranus" "Neptune" "Pluto"]
IncludeSRP: 0
PlanetaryEphemerisModel: "de405"
Calculate Initial Osculating Elements
Define the initial position and velocity of the spacecraft in ICRF. These represent the spacecraft states immediately after the translunar injection burn. Calculation of these states is out of scope of this example, but can be calculated using nonlinear constrained optimization techniques to minimize initial velocity magnitude.
initialPosition = ... [5927630.386747557; ... 3087663.891097251; ... 1174446.969646237]; % m initialVelocity = ... [-5190.330300215130; ... 8212.486957313564; ... 4605.538019512981]; % m/s
Convert the ICRF position and velocity to osculating elements. The osculating elements are the instantaneous Keplerian elements corresponding to the orbit that the spacecraft would follow if the perturbations were to be ignored.
[semiMajorAxis, ... eccentricity, ... inclination, ... rightAscensionOfAscendingNode, ... argumentOfPeriapsis, ... trueAnomaly] = ijk2keplerian(initialPosition,initialVelocity)
semiMajorAxis =
2.118144315642977e+08
eccentricity = 0.967962522906465
inclination = 27.516388036479892
rightAscensionOfAscendingNode = 7.800979911647819
argumentOfPeriapsis = 21.999999999999996
trueAnomaly =
0
Add Spacecraft to Scenario
Use the satellite function to add a spacecraft to the scenario using the calculated osculating elements. Assign the numerical propagator to the spacecraft.
craft = satellite(sc, ... semiMajorAxis, ... eccentricity, ... inclination, ... rightAscensionOfAscendingNode, ... argumentOfPeriapsis, ... trueAnomaly, ... OrbitPropagator="numerical", ... Name="Spacecraft")
craft =
Satellite with properties:
Name: Spacecraft
ID: 1
PhysicalProperties: [1x1 Aero.satellitescenario.satellite.PhysicalProperties]
ConicalSensors: [1x0 matlabshared.satellitescenario.ConicalSensor]
Gimbals: [1x0 matlabshared.satellitescenario.Gimbal]
Transmitters: [1x0 satcom.satellitescenario.Transmitter]
Receivers: [1x0 satcom.satellitescenario.Receiver]
Accesses: [1x0 matlabshared.satellitescenario.Access]
Eclipse: [1x0 Aero.satellitescenario.Eclipse]
GroundTrack: [1x1 matlabshared.satellitescenario.GroundTrack]
Orbit: [1x1 matlabshared.satellitescenario.Orbit]
CoordinateAxes: [1x1 matlabshared.satellitescenario.CoordinateAxes]
OrbitPropagator: numerical
MarkerColor: [0.059 1 1]
MarkerSize: 6
ShowLabel: true
LabelFontColor: [1 1 1]
LabelFontSize: 15
Visual3DModel:
Visual3DModelScale: 1
The property PhysicalProperties defines the physical characteristics of the spacecraft used by atmospheric drag and solar radiation pressure calculations. These characteristics currently use default values and are unused because atmospheric drag and solar radiation pressure are ignored in this example.
craft.physicalProperties
ans =
PhysicalProperties with properties:
Mass: 4
DragCoefficient: 2.179000000000000
DragArea: 1
ReflectivityCoefficient: 1.800000000000000
SRPArea: 1
Add Moon to Scenario
The satellite scenario viewer used for visualizing the scenario already renders visualization for the moon. However, you can gain better situational awareness if the lunar orbit is plotted as well. To do this, add a satellite to the scenario using the satellite function that is on the same trajectory as that of the Moon. To calculate the trajectory of the Moon, start by computing the barycentric dynamical times (TDB) for the scenario time samples as Julian dates.
utc = startTime:seconds(60):stopTime; leapSeconds = 37; % s ttMinusTAI = 32.184; % s terrestrialTime = utc + seconds(leapSeconds + ttMinusTAI); tdbJD = tdbjuliandate([ ... terrestrialTime.Year' ... terrestrialTime.Month' ... terrestrialTime.Day' ... terrestrialTime.Hour' ... terrestrialTime.Minute' ... terrestrialTime.Second']);
Calculate the positions of the Moon for each scenario time sample using planetEphemeris and convert the positions into a timetable.
pMoonkm = planetEphemeris(tdbJD,"earth","moon"); % km pMoon = convlength(pMoonkm,'km','m'); % m pMoonTT = timetable(utc',pMoon);
Add a satellite representing the Moon to the scenario using the satellite function. Set the orbit and marker color to red.
moon = satellite(sc,pMoonTT,Name="Moon"); moon.Orbit.LineColor="red"; moon.MarkerColor="red";
Label Earth
The scale of the distance involved in the scenario is large enough that the Earth may not be readily visible when viewing from the shadow side. To mitigate this, add a ground station at the North pole of the Earth and label it "Earth". Set the marker size of this ground station to 0.001. This way, the label "Earth" will be visible near the position of the Earth.
earth = groundStation(sc, ... 90, ... % Latitude, deg 0, ... % Longitude, deg Name="Earth"); earth.MarkerSize = 0.001;
Visualize Scenario
Run satelliteScenarioViewer to launch a satellite scenario viewer. Set the playback speed multiplier to 60,000. Set the camera reference frame to "inertial".
v = satelliteScenarioViewer(sc, ... CameraReferenceFrame="Inertial", ... PlaybackSpeedMultiplier=60000);
Set the camera position and orientation to visualize the free-return trajectory. from a top-down view
campos(v, ... 55.991361, ... % Latitude, deg 18.826434, ... % Longitude, deg 1163851259.541816); % Altitude, m camheading(v, ... 359.7544952991605); % deg campitch(v, ... -89.830968253450209); % deg camroll(v, ... 0); % deg
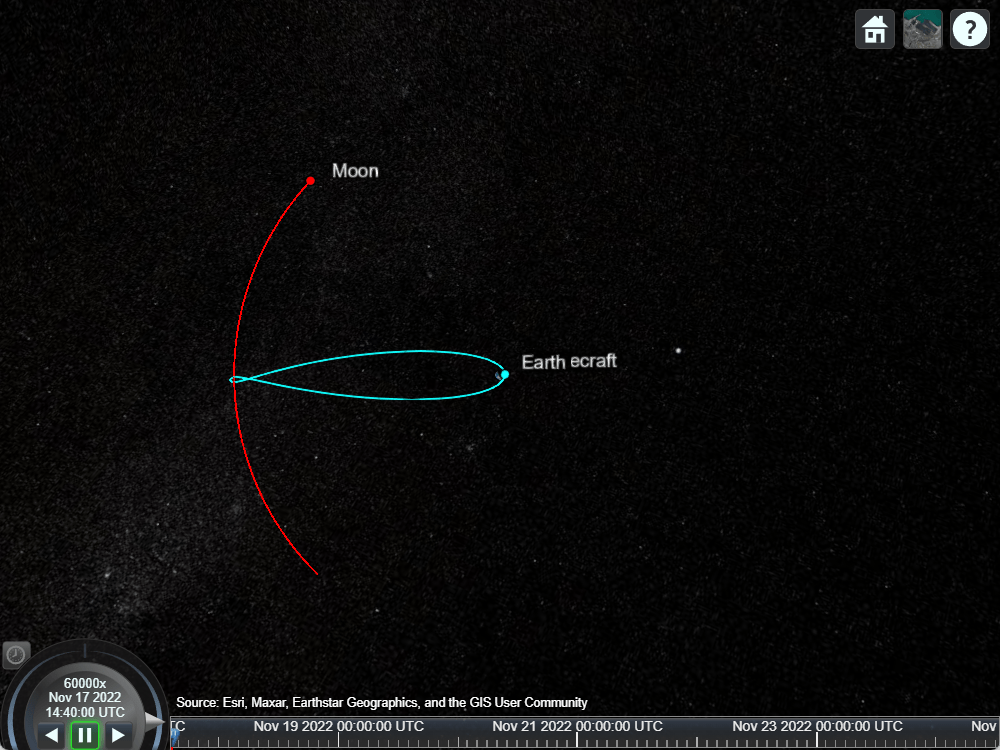
Play the scenario.
play(sc);
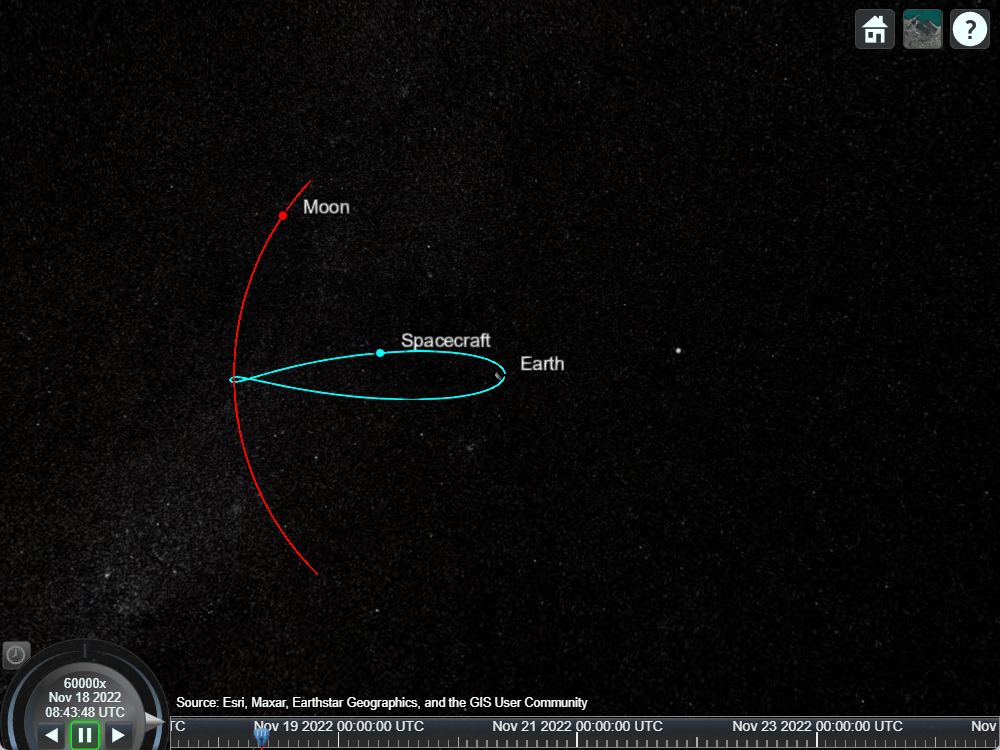
Manually re-position the camera to get a better view of the lunar encounter. Use left-click-drag to rotate and right-click-drag to translate forward and back. Alternatively, you can also use the scroll wheel to translate forward and back.
See Also
Objects
Functions
Related Topics
You can also select a web site from the following list
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)
Asia Pacific
- Australia (English)
- India (English)
- New Zealand (English)
- 中国
- 日本Japanese (日本語)
- 한국Korean (한국어)