Exploring Genome-Wide Differences in DNA Methylation Profiles
This example shows how to perform a genome-wide analysis of DNA methylation in the human by using genome sequencing.
Note: For enhanced performance, MathWorks recommends that you run this example on a 64-bit platform, because the memory footprint is close to 2 GB. On a 32-bit platform, if you receive "Out of memory" errors when running this example, try increasing the virtual memory (or swap space) of your operating system or try setting the 3GB switch (32-bit Windows® XP only). For details, see Resolve “Out of Memory” Errors.
Introduction
DNA methylation is an epigenetic modification that modulates gene expression and the maintenance of genomic organization in normal and disease processes. DNA methylation can define different states of the cell, and it is inheritable during cell replication. Aberrant DNA methylation patterns have been associated with cancer and tumor suppressor genes.
In this example you will explore the DNA methylation profiles of two human cancer cells: parental HCT116 colon cancer cells and DICERex5 cells. DICERex5 cells are derived from HCT116 cells after the truncation of the DICER1 alleles. Serre et al. in [1] proposed to study DNA methylation profiles by using the MBD2 protein as a methyl CpG binding domain and subsequently used high-throughput sequencing (HTseq). This technique is commonly known as MBD-Seq. Short reads for two replicates of the two samples have been submitted to NCBI's SRA archive by the authors of [1]. There are other technologies available to interrogate DNA methylation status of CpG sites in combination with HTseq, for example MeDIP-seq or the use of restriction enzymes. You can also analyze this type of data sets following the approach presented in this example.
Data Sets
You can obtain the unmapped single-end reads for four sequencing experiments from NCBI. Short reads were produced using Illumina®'s Genome Analyzer II. Average insert size is 120 bp, and the length of short reads is 36 bp.
This example assumes that you:
(1) downloaded the files SRR030222.sra, SRR030223.sra, SRR030224.sra and SRR030225.sra containing the unmapped short reads for two replicates of from the DICERex5 sample and two replicates from the HCT116 sample respectively, from NCBI SRA Run Selector and converted them to FASTQ-formatted files using the NCBI SRA Toolkit.
(2) produced SAM-formatted files by mapping the short reads to the reference human genome (NCBI Build 37.5) using the Bowtie [2] algorithm. Only uniquely mapped reads are reported.
(3) compressed the SAM formatted files to BAM and ordered them by reference name first, then by genomic position by using SAMtools [3].
This example also assumes that you downloaded the reference human genome (GRCh37.p5). You can use the bowtie-inspect command to reconstruct the human reference directly from the bowtie indices. Or you may download the reference from the NCBI repository by uncommenting the following line:
% getgenbank('NC_000009','FileFormat','fasta','tofile','hsch9.fasta');
Creating a MATLAB® Interface to the BAM-Formatted Files
To explore the signal coverage of the HCT116 samples you need to construct a BioMap. BioMap has an interface that provides direct access to the mapped short reads stored in the BAM-formatted file, thus minimizing the amount of data that is actually loaded into memory. Use the function baminfo to obtain a list of the existing references and the actual number of short reads mapped to each one.
info = baminfo('SRR030224.bam','ScanDictionary',true); fprintf('%-35s%s\n','Reference','Number of Reads'); for i = 1:numel(info.ScannedDictionary) fprintf('%-35s%d\n',info.ScannedDictionary{i},... info.ScannedDictionaryCount(i)); end
Reference Number of Reads gi|224589800|ref|NC_000001.10| 205065 gi|224589811|ref|NC_000002.11| 187019 gi|224589815|ref|NC_000003.11| 73986 gi|224589816|ref|NC_000004.11| 84033 gi|224589817|ref|NC_000005.9| 96898 gi|224589818|ref|NC_000006.11| 87990 gi|224589819|ref|NC_000007.13| 120816 gi|224589820|ref|NC_000008.10| 111229 gi|224589821|ref|NC_000009.11| 106189 gi|224589801|ref|NC_000010.10| 112279 gi|224589802|ref|NC_000011.9| 104466 gi|224589803|ref|NC_000012.11| 87091 gi|224589804|ref|NC_000013.10| 53638 gi|224589805|ref|NC_000014.8| 64049 gi|224589806|ref|NC_000015.9| 60183 gi|224589807|ref|NC_000016.9| 146868 gi|224589808|ref|NC_000017.10| 195893 gi|224589809|ref|NC_000018.9| 60344 gi|224589810|ref|NC_000019.9| 166420 gi|224589812|ref|NC_000020.10| 148950 gi|224589813|ref|NC_000021.8| 310048 gi|224589814|ref|NC_000022.10| 76037 gi|224589822|ref|NC_000023.10| 32421 gi|224589823|ref|NC_000024.9| 18870 gi|17981852|ref|NC_001807.4| 1015 Unmapped 6805842
In this example you will focus on the analysis of chromosome 9. Create a BioMap for the two HCT116 sample replicates.
bm_hct116_1 = BioMap('SRR030224.bam','SelectRef','gi|224589821|ref|NC_000009.11|') bm_hct116_2 = BioMap('SRR030225.bam','SelectRef','gi|224589821|ref|NC_000009.11|')
bm_hct116_1 =
BioMap with properties:
SequenceDictionary: 'gi|224589821|ref|NC_000009.11|'
Reference: [106189x1 File indexed property]
Signature: [106189x1 File indexed property]
Start: [106189x1 File indexed property]
MappingQuality: [106189x1 File indexed property]
Flag: [106189x1 File indexed property]
MatePosition: [106189x1 File indexed property]
Quality: [106189x1 File indexed property]
Sequence: [106189x1 File indexed property]
Header: [106189x1 File indexed property]
NSeqs: 106189
Name: ''
bm_hct116_2 =
BioMap with properties:
SequenceDictionary: 'gi|224589821|ref|NC_000009.11|'
Reference: [107586x1 File indexed property]
Signature: [107586x1 File indexed property]
Start: [107586x1 File indexed property]
MappingQuality: [107586x1 File indexed property]
Flag: [107586x1 File indexed property]
MatePosition: [107586x1 File indexed property]
Quality: [107586x1 File indexed property]
Sequence: [107586x1 File indexed property]
Header: [107586x1 File indexed property]
NSeqs: 107586
Name: ''
Using a binning algorithm provided by the getBaseCoverage method, you can plot the coverage of both replicates for an initial inspection. For reference, you can also add the ideogram for the human chromosome 9 to the plot using the chromosomeplot function.
figure ha = gca; hold on n = 141213431; % length of chromosome 9 [cov,bin] = getBaseCoverage(bm_hct116_1,1,n,'binWidth',100); h1 = plot(bin,cov,'b'); % plots the binned coverage of bm_hct116_1 [cov,bin] = getBaseCoverage(bm_hct116_2,1,n,'binWidth',100); h2 = plot(bin,cov,'g'); % plots the binned coverage of bm_hct116_2 chromosomeplot('hs_cytoBand.txt', 9, 'AddToPlot', ha) % plots an ideogram along the x-axis axis(ha,[1 n 0 100]) % zooms-in the y-axis fixGenomicPositionLabels(ha) % formats tick labels and adds datacursors legend([h1 h2],'HCT116-1','HCT116-2','Location','NorthEast') ylabel('Coverage') title('Coverage for two replicates of the HCT116 sample') fig = gcf; fig.Position = max(fig.Position,[0 0 900 0]); % resize window
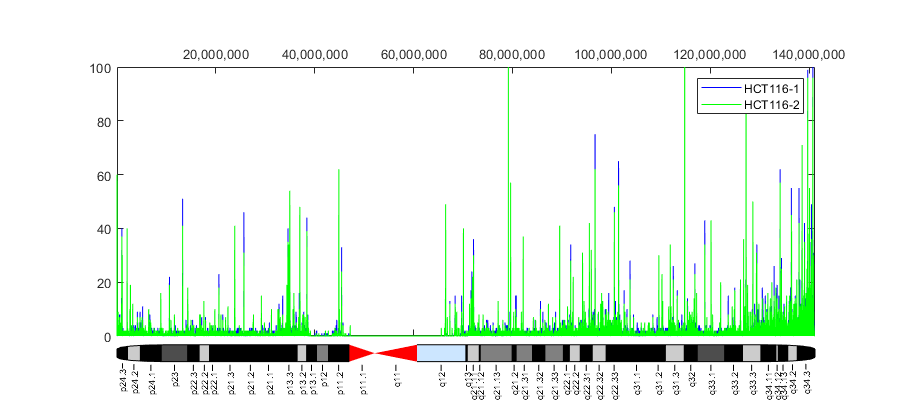
Because short reads represent the methylated regions of the DNA, there is a correlation between aligned coverage and DNA methylation. Observe the increased DNA methylation close to the chromosome telomeres; it is known that there is an association between DNA methylation and the role of telomeres for maintaining the integrity of the chromosomes. In the coverage plot you can also see a long gap over the chromosome centromere. This is due to the repetitive sequences present in the centromere, which prevent us from aligning short reads to a unique position in this region. In the data sets used in this example only about 30% of the short reads were uniquely mapped to the reference genome.
Correlating CpG Islands and DNA Methylation
DNA methylation normally occurs in CpG dinucleotides. Alteration of the DNA methylation patterns can lead to transcriptional silencing, especially in the gene promoter CpG islands. But, it is also known that DNA methylation can block CTCF binding and can silence miRNA transcription among other relevant functions. In general, it is expected that mapped reads should preferably align to CpG rich regions.
Load the human chromosome 9 from the reference file hs37.fasta. For this example, it is assumed that you recovered the reference from the Bowtie indices using the bowtie-inspect command; therefore hs37.fasta contains all the human chromosomes. To load only the chromosome 9 you can use the option nave-value pair BLOCKREAD with the fastaread function.
chr9 = fastaread('hs37.fasta','blockread',9); chr9.Header
ans =
'gi|224589821|ref|NC_000009.11| Homo sapiens chromosome 9, GRCh37 primary reference assembly'
Use the cpgisland function to find the CpG clusters. Using the standard definition for CpG islands [4], 200 or more bp islands with 60% or greater CpGobserved/CpGexpected ratio, leads to 1682 GpG islands found in chromosome 9.
cpgi = cpgisland(chr9.Sequence)
cpgi =
struct with fields:
Starts: [10783 29188 73049 73686 113309 114488 116877 … ] (1×1682 double)
Stops: [11319 29409 73624 73893 114336 114809 117105 … ] (1×1682 double)
Use the getCounts method to calculate the ratio of aligned bases that are inside CpG islands. For the first replicate of the sample HCT116, the ratio is close to 45%.
aligned_bases_in_CpG_islands = getCounts(bm_hct116_1,cpgi.Starts,cpgi.Stops,'method','sum') aligned_bases_total = getCounts(bm_hct116_1,1,n,'method','sum') ratio = aligned_bases_in_CpG_islands ./ aligned_bases_total
aligned_bases_in_CpG_islands =
1724363
aligned_bases_total =
3822804
ratio =
0.4511
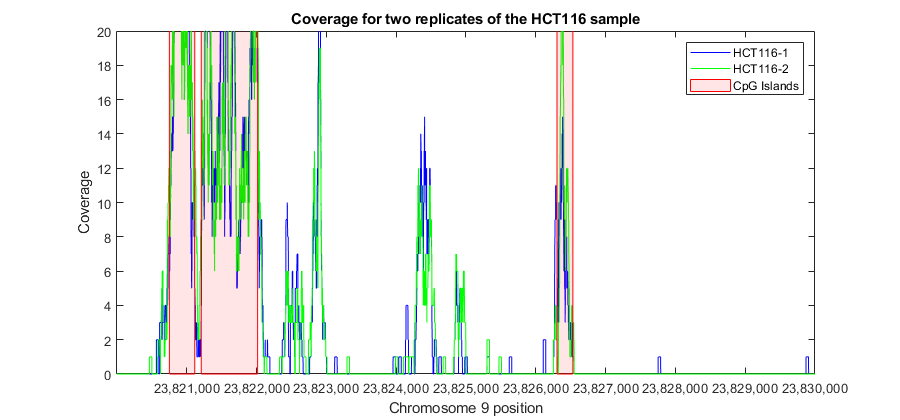
You can explore high resolution coverage plots of the two sample replicates and observe how the signal correlates with the CpG islands. For example, explore the region between 23,820,000 and 23,830,000 bp. This is the 5' region of the human gene ELAVL2.
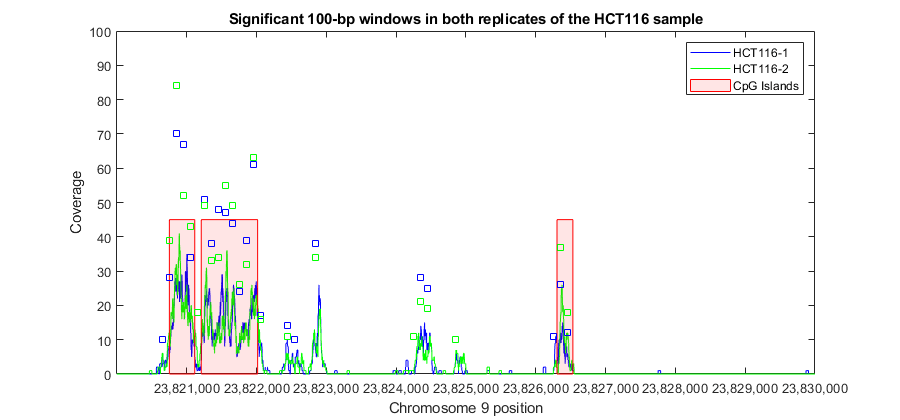
r1 = 23820001; % set the region limits r2 = 23830000; fhELAVL2 = figure; % keep the figure handle to use it later hold on % plot high-resolution coverage of bm_hct116_1 h1 = plot(r1:r2,getBaseCoverage(bm_hct116_1,r1,r2,'binWidth',1),'b'); % plot high-resolution coverage of bm_hct116_2 h2 = plot(r1:r2,getBaseCoverage(bm_hct116_2,r1,r2,'binWidth',1),'g'); % mark the CpG islands within the [r1 r2] region for i = 1:numel(cpgi.Starts) if cpgi.Starts(i)>r1 && cpgi.Stops(i)<r2 % is CpG island inside [r1 r2]? px = [cpgi.Starts([i i]) cpgi.Stops([i i])]; % x-coordinates for patch py = [0 max(ylim) max(ylim) 0]; % y-coordinates for patch hp = patch(px,py,'r','FaceAlpha',.1,'EdgeColor','r','Tag','cpgi'); end end axis([r1 r2 0 20]) % zooms-in the y-axis fixGenomicPositionLabels(gca) % formats tick labels and adds datacursors legend([h1 h2 hp],'HCT116-1','HCT116-2','CpG Islands') ylabel('Coverage') xlabel('Chromosome 9 position') title('Coverage for two replicates of the HCT116 sample')
Statistical Modelling of Count Data
To find regions that contain more mapped reads than would be expected by chance, you can follow a similar approach to the one described by Serre et al. [1]. The number of counts for non-overlapping contiguous 100 bp windows is statistically modeled.
First, use the getCounts method to count the number of mapped reads that start at each window. In this example you use a binning approach that considers only the start position of every mapped read, following the approach of Serre et al. However, you may also use the OVERLAP and METHOD name-value pairs in getCounts to compute more accurate statistics. For instance, to obtain the maximum coverage for each window considering base pair resolution, set OVERLAP to 1 and METHOD to MAX.
n = numel(chr9.Sequence); % length of chromosome w = 1:100:n; % windows of 100 bp counts_1 = getCounts(bm_hct116_1,w,w+99,'independent',true,'overlap','start'); counts_2 = getCounts(bm_hct116_2,w,w+99,'independent',true,'overlap','start');
First, try to model the counts assuming that all the windows with counts are biologically significant and therefore from the same distribution. Use the negative bionomial distribution to fit a model the count data.
nbp = nbinfit(counts_1);
Plot the fitted model over a histogram of the empirical data.
figure hold on edges = 0:100; emphist = histcounts(counts_1,edges); % calculate the empirical distribution binCenters = (edges(1:end-1) + edges(2:end)) / 2; bar(binCenters,emphist./sum(emphist),'c','grouped') % plot histogram plot(0:100,nbinpdf(0:100,nbp(1),nbp(2)),'b','linewidth',2); % plot fitted model axis([0 50 0 .001]) legend('Empirical Distribution','Negative Binomial Fit') ylabel('Frequency') xlabel('Counts') title('Frequency of counts, 100bp windows (HCT116-1)')
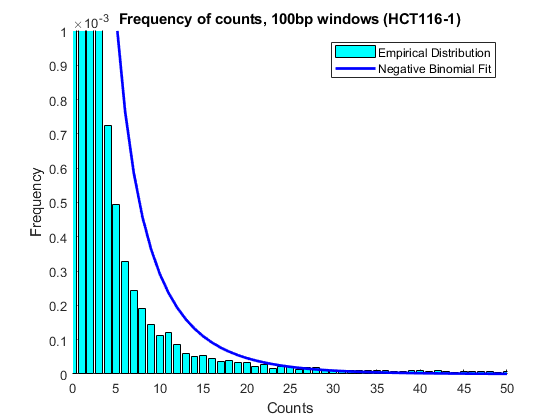
The poor fitting indicates that the observed distribution may be due to the mixture of two models, one that represents the background and one that represents the count data in methylated DNA windows.
A more realistic scenario would be to assume that windows with a small number of mapped reads are mainly the background (or null model). Serre et al. assumed that 100-bp windows containing four or more reads are unlikely to be generated by chance. To estimate a good approximation to the null model, you can fit the left body of the empirical distribution to a truncated negative binomial distribution. To fit a truncated distribution use the mle function. First you need to define an anonymous function that defines the right-truncated version of nbinpdf.
rtnbinpdf = @(x,p1,p2,t) nbinpdf(x,p1,p2) ./ nbincdf(t-1,p1,p2);
Define the fitting function using another anonymous function.
rtnbinfit = @(x2,t) mle(x2,'pdf',@(x3,p1,p2) rtnbinpdf(x3,p1,p2,t),'start',nbinfit(x2),'lower',[0 0]);
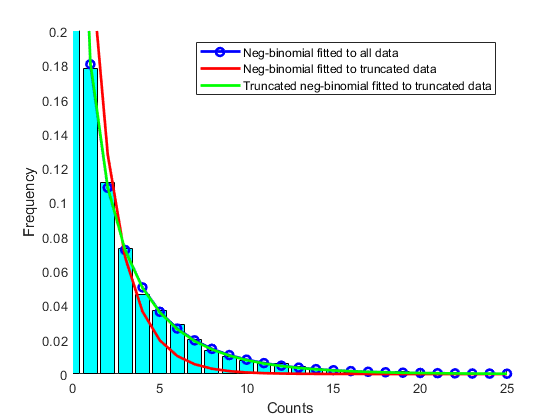
Before fitting the real data, let us assess the fitting procedure with some sampled data from a known distribution.
nbp = [0.5 0.2]; % Known coefficients x = nbinrnd(nbp(1),nbp(2),10000,1); % Random sample trun = 6; % Set a truncation threshold nbphat1 = nbinfit(x); % Fit non-truncated model to all data nbphat2 = nbinfit(x(x<trun)); % Fit non-truncated model to truncated data (wrong) nbphat3 = rtnbinfit(x(x<trun),trun); % Fit truncated model to truncated data figure hold on edges = 0:100; emphist = histcounts(x,edges); % Calculate the empirical distribution binCenters = (edges(1:end-1) + edges(2:end)) / 2; bar(binCenters,emphist./sum(emphist),'c','grouped') % plot histogram h1 = plot(0:100,nbinpdf(0:100,nbphat1(1),nbphat1(2)),'b-o','linewidth',2); h2 = plot(0:100,nbinpdf(0:100,nbphat2(1),nbphat2(2)),'r','linewidth',2); h3 = plot(0:100,nbinpdf(0:100,nbphat3(1),nbphat3(2)),'g','linewidth',2); axis([0 25 0 .2]) legend([h1 h2 h3],'Neg-binomial fitted to all data',... 'Neg-binomial fitted to truncated data',... 'Truncated neg-binomial fitted to truncated data') ylabel('Frequency') xlabel('Counts')
Identifying Significant Methylated Regions
For the two replicates of the HCT116 sample, fit a right-truncated negative binomial distribution to the observed null model using the rtnbinfit anonymous function previously defined.
trun = 4; % Set a truncation threshold (as in [1]) pn1 = rtnbinfit(counts_1(counts_1<trun),trun); % Fit to HCT116-1 counts pn2 = rtnbinfit(counts_2(counts_2<trun),trun); % Fit to HCT116-2 counts
Calculate the p-value for each window to the null distribution.
pval1 = 1 - nbincdf(counts_1,pn1(1),pn1(2)); pval2 = 1 - nbincdf(counts_2,pn2(1),pn2(2));
Calculate the false discovery rate using the mafdr function. Use the name-value pair BHFDR to use the linear-step up (LSU) procedure ([6]) to calculate the FDR adjusted p-values. Setting the FDR < 0.01 permits you to identify the 100-bp windows that are significantly methylated.
fdr1 = mafdr(pval1,'bhfdr',true); fdr2 = mafdr(pval2,'bhfdr',true); w1 = fdr1<.01; % logical vector indicating significant windows in HCT116-1 w2 = fdr2<.01; % logical vector indicating significant windows in HCT116-2 w12 = w1 & w2; % logical vector indicating significant windows in both replicates Number_of_sig_windows_HCT116_1 = sum(w1) Number_of_sig_windows_HCT116_2 = sum(w2) Number_of_sig_windows_HCT116 = sum(w12)
Number_of_sig_windows_HCT116_1 =
1662
Number_of_sig_windows_HCT116_2 =
1674
Number_of_sig_windows_HCT116 =
1346
Overall, you identified 1662 and 1674 non-overlapping 100-bp windows in the two replicates of the HCT116 samples, which indicates there is significant evidence of DNA methylation. There are 1346 windows that are significant in both replicates.
For example, looking again in the promoter region of the ELAVL2 human gene you can observe that in both sample replicates, multiple 100-bp windows have been marked significant.
figure(fhELAVL2) % bring back to focus the previously plotted figure plot(w(w1)+50,counts_1(w1),'bs', 'HandleVisibility','off') % plot significant windows in HCT116-1 plot(w(w2)+50,counts_2(w2),'gs', 'HandleVisibility','off') % plot significant windows in HCT116-2 axis([r1 r2 0 100]) title('Significant 100-bp windows in both replicates of the HCT116 sample')
Finding Genes With Significant Methylated Promoter Regions
DNA methylation is involved in the modulation of gene expression. For instance, it is well known that hypermethylation is associated with the inactivation of several tumor suppressor genes. You can study in this data set the methylation of gene promoter regions.
First, download from Ensembl a tab-separated-value (TSV) table with all protein encoding genes to a text file, ensemblmart_genes_hum37.txt. For this example, we are using Ensembl release 64. Using Ensembl's BioMart service, you can select a table with the following attributes: chromosome name, gene biotype, gene name, gene start/end, and strand direction.
Use the provided helper function ensemblmart2gff to convert the downloaded TSV file to a GFF formatted file. Then use GFFAnnotation to load the file into MATLAB and create a subset with the genes present in chromosome 9 only. This results 800 annotated protein-coding genes in the Ensembl database.
GFFfilename = ensemblmart2gff('ensemblmart_genes_hum37.txt'); a = GFFAnnotation(GFFfilename) a9 = getSubset(a,'reference','9') numGenes = a9.NumEntries
a =
GFFAnnotation with properties:
FieldNames: {1×9 cell}
NumEntries: 21184
a9 =
GFFAnnotation with properties:
FieldNames: {1×9 cell}
NumEntries: 800
numGenes =
800
Find the promoter regions for each gene. In this example we consider the proximal promoter as the -500/100 upstream region.
downstream = 500; upstream = 100; geneDir = strcmp(a9.Strand,'+'); % logical vector indicating strands in the forward direction % calculate promoter's start position for genes in the forward direction promoterStart(geneDir) = a9.Start(geneDir) - downstream; % calculate promoter's end position for genes in the forward direction promoterStop(geneDir) = a9.Start(geneDir) + upstream; % calculate promoter's start position for genes in the reverse direction promoterStart(~geneDir) = a9.Stop(~geneDir) - upstream; % calculate promoter's end position for genes in the reverse direction promoterStop(~geneDir) = a9.Stop(~geneDir) + downstream;
Use a dataset as a container for the promoter information, as we can later add new columns to store gene counts and p-values.
promoters = dataset({a9.Feature,'Gene'});
promoters.Strand = char(a9.Strand);
promoters.Start = promoterStart';
promoters.Stop = promoterStop';
Find genes with significant DNA methylation in the promoter region by looking at the number of mapped short reads that overlap at least one base pair in the defined promoter region.
promoters.Counts_1 = getCounts(bm_hct116_1,promoters.Start,promoters.Stop,... 'overlap',1,'independent',true); promoters.Counts_2 = getCounts(bm_hct116_2,promoters.Start,promoters.Stop,... 'overlap',1,'independent',true);
Fit a null distribution for each sample replicate and compute the p-values:
trun = 5; % Set a truncation threshold pn1 = rtnbinfit(promoters.Counts_1(promoters.Counts_1<trun),trun); % Fit to HCT116-1 promoter counts pn2 = rtnbinfit(promoters.Counts_2(promoters.Counts_2<trun),trun); % Fit to HCT116-2 promoter counts promoters.pval_1 = 1 - nbincdf(promoters.Counts_1,pn1(1),pn1(2)); % p-value for every promoter in HCT116-1 promoters.pval_2 = 1 - nbincdf(promoters.Counts_2,pn2(1),pn2(2)); % p-value for every promoter in HCT116-2 Number_of_sig_promoters = sum(promoters.pval_1<.01 & promoters.pval_2<.01) Ratio_of_sig_methylated_promoters = Number_of_sig_promoters./numGenes
Number_of_sig_promoters =
74
Ratio_of_sig_methylated_promoters =
0.0925
Observe that only 74 (out of 800) genes in chromosome 9 have significantly DNA methylated regions (pval<0.01 in both replicates). Display a report of the 30 genes with the most significant methylated promoter regions.
[~,order] = sort(promoters.pval_1.*promoters.pval_2); promoters(order(1:30),[1 2 3 4 5 7 6 8])
ans =
Gene Strand Start Stop Counts_1
{'DMRT3' } + 976464 977064 223
{'CNTFR' } - 34590021 34590621 219
{'GABBR2' } - 101471379 101471979 404
{'CACNA1B' } + 140771741 140772341 454
{'BARX1' } - 96717554 96718154 264
{'FAM78A' } - 134151834 134152434 497
{'FOXB2' } + 79634071 79634671 163
{'TLE4' } + 82186188 82186788 157
{'ASTN2' } - 120177248 120177848 141
{'FOXE1' } + 100615036 100615636 149
{'MPDZ' } - 13279489 13280089 129
{'PTPRD' } - 10612623 10613223 145
{'PALM2-AKAP2'} + 112542089 112542689 134
{'FAM69B' } + 139606522 139607122 112
{'WNK2' } + 95946698 95947298 108
{'IGFBPL1' } - 38424344 38424944 110
{'AKAP2' } + 112542269 112542869 107
{'C9orf4' } - 111929471 111930071 102
{'COL5A1' } + 137533120 137533720 84
{'LHX3' } - 139096855 139097455 74
{'OLFM1' } + 137966768 137967368 75
{'NPR2' } + 35791651 35792251 68
{'DBC1' } - 122131645 122132245 61
{'SOHLH1' } - 138591274 138591874 56
{'PIP5K1B' } + 71320075 71320675 59
{'PRDM12' } + 133539481 133540081 53
{'ELAVL2' } - 23826235 23826835 50
{'ZFP37' } - 115818939 115819539 59
{'RP11-35N6.1'} + 103790491 103791091 60
{'DMRT2' } + 1049854 1050454 54
pval_1 Counts_2 pval_2
6.6613e-16 253 5.5511e-16
6.6613e-16 226 5.5511e-16
6.6613e-16 400 5.5511e-16
6.6613e-16 408 5.5511e-16
6.6613e-16 286 5.5511e-16
6.6613e-16 499 5.5511e-16
1.4e-13 165 6.0352e-13
3.5649e-13 151 4.7347e-12
4.3566e-12 163 8.0969e-13
1.2447e-12 133 6.7598e-11
2.8679e-11 148 7.3682e-12
2.3279e-12 127 1.6448e-10
1.3068e-11 135 5.0276e-11
4.1911e-10 144 1.3295e-11
7.897e-10 125 2.2131e-10
5.7523e-10 114 1.1364e-09
9.2538e-10 106 3.7513e-09
2.0467e-09 96 1.6795e-08
3.6266e-08 97 1.4452e-08
1.8171e-07 91 3.5644e-08
1.5457e-07 69 1.0074e-06
4.8093e-07 73 5.4629e-07
1.5082e-06 62 2.9575e-06
3.4322e-06 67 1.3692e-06
2.0943e-06 63 2.5345e-06
5.6364e-06 61 3.4518e-06
9.2778e-06 62 2.9575e-06
2.0943e-06 47 3.0746e-05
1.7771e-06 42 6.8037e-05
4.7762e-06 46 3.6016e-05
Finding Intergenic Regions that are Significantly Methylated
Serre et al. [1] reported that, in these data sets, approximately 90% of the uniquely mapped reads fall outside the 5' gene promoter regions. Using a similar approach as before, you can find genes that have intergenic methylated regions. To compensate for the varying lengths of the genes, you can use the maximum coverage, computed base-by-base, instead of the raw number of mapped short reads. Another alternative approach to normalize the counts by the gene length is to set the METHOD name-value pair to rpkm in the getCounts function.
intergenic = dataset({a9.Feature,'Gene'});
intergenic.Strand = char(a9.Strand);
intergenic.Start = a9.Start;
intergenic.Stop = a9.Stop;
intergenic.Counts_1 = getCounts(bm_hct116_1,intergenic.Start,intergenic.Stop,...
'overlap','full','method','max','independent',true);
intergenic.Counts_2 = getCounts(bm_hct116_2,intergenic.Start,intergenic.Stop,...
'overlap','full','method','max','independent',true);
trun = 10; % Set a truncation threshold
pn1 = rtnbinfit(intergenic.Counts_1(intergenic.Counts_1<trun),trun); % Fit to HCT116-1 intergenic counts
pn2 = rtnbinfit(intergenic.Counts_2(intergenic.Counts_2<trun),trun); % Fit to HCT116-2 intergenic counts
intergenic.pval_1 = 1 - nbincdf(intergenic.Counts_1,pn1(1),pn1(2)); % p-value for every intergenic region in HCT116-1
intergenic.pval_2 = 1 - nbincdf(intergenic.Counts_2,pn2(1),pn2(2)); % p-value for every intergenic region in HCT116-2
Number_of_sig_genes = sum(intergenic.pval_1<.01 & intergenic.pval_2<.01)
Ratio_of_sig_methylated_genes = Number_of_sig_genes./numGenes
[~,order] = sort(intergenic.pval_1.*intergenic.pval_2);
intergenic(order(1:30),[1 2 3 4 5 7 6 8])
Number_of_sig_genes =
62
Ratio_of_sig_methylated_genes =
0.0775
ans =
Gene Strand Start Stop Counts_1
{'AL772363.1'} - 140762377 140787022 106
{'CACNA1B' } + 140772241 141019076 106
{'SUSD1' } - 114803065 114937688 88
{'C9orf172' } + 139738867 139741797 99
{'NR5A1' } - 127243516 127269709 86
{'BARX1' } - 96713628 96717654 77
{'KCNT1' } + 138594031 138684992 58
{'GABBR2' } - 101050391 101471479 65
{'FOXB2' } + 79634571 79635869 51
{'NDOR1' } + 140100119 140113813 54
{'KIAA1045' } + 34957484 34984679 50
{'ADAMTSL2' } + 136397286 136440641 55
{'PAX5' } - 36833272 37034476 48
{'OLFM1' } + 137967268 138013025 55
{'PBX3' } + 128508551 128729656 45
{'FOXE1' } + 100615536 100618986 49
{'MPDZ' } - 13105703 13279589 51
{'ASTN2' } - 119187504 120177348 43
{'ARRDC1' } + 140500106 140509812 49
{'IGFBPL1' } - 38408991 38424444 45
{'LHX3' } - 139088096 139096955 44
{'PAPPA' } + 118916083 119164601 44
{'CNTFR' } - 34551430 34590121 41
{'DMRT3' } + 976964 991731 40
{'TUSC1' } - 25676396 25678856 46
{'ELAVL2' } - 23690102 23826335 35
{'SMARCA2' } + 2015342 2193624 36
{'GAS1' } - 89559279 89562104 34
{'GRIN1' } + 140032842 140063207 36
{'TLE4' } + 82186688 82341658 36
pval_1 Counts_2 pval_2
8.6597e-15 98 1.8763e-14
8.6597e-15 98 1.8763e-14
2.2904e-12 112 7.7716e-16
7.4718e-14 96 3.5749e-14
4.268e-12 90 2.5457e-13
7.0112e-11 62 2.569e-09
2.5424e-08 73 6.9019e-11
2.9078e-09 58 9.5469e-09
2.2131e-07 58 9.5469e-09
8.7601e-08 55 2.5525e-08
3.0134e-07 55 2.5525e-08
6.4307e-08 45 6.7163e-07
5.585e-07 49 1.8188e-07
6.4307e-08 42 1.7861e-06
1.4079e-06 51 9.4566e-08
4.1027e-07 46 4.8461e-07
2.2131e-07 42 1.7861e-06
2.6058e-06 43 1.2894e-06
4.1027e-07 36 1.2564e-05
1.4079e-06 39 4.7417e-06
1.9155e-06 36 1.2564e-05
1.9155e-06 35 1.7377e-05
4.8199e-06 37 9.0815e-06
6.5537e-06 37 9.0815e-06
1.0346e-06 31 6.3417e-05
3.0371e-05 41 2.4736e-06
2.2358e-05 40 3.4251e-06
4.1245e-05 41 2.4736e-06
2.2358e-05 38 6.5629e-06
2.2358e-05 37 9.0815e-06
For instance, explore the methylation profile of the BARX1 gene, the sixth significant gene with intergenic methylation in the previous list. The GTF formatted file ensemblmart_barx1.gtf contains structural information for this gene obtained from Ensembl using the BioMart service.
Use GTFAnnotation to load the structural information into MATLAB. There are two annotated transcripts for this gene.
barx1 = GTFAnnotation('ensemblmart_barx1.gtf')
transcripts = getTranscriptNames(barx1)
barx1 =
GTFAnnotation with properties:
FieldNames: {1×11 cell}
NumEntries: 18
transcripts =
2×1 cell array
{'ENST00000253968'}
{'ENST00000401724'}
Plot the DNA methylation profile for both HCT116 sample replicates with base-pair resolution. Overlay the CpG islands and plot the exons for each of the two transcripts along the bottom of the plot.
range = barx1.getRange; r1 = range(1)-1000; % set the region limits r2 = range(2)+1000; figure hold on % plot high-resolution coverage of bm_hct116_1 h1 = plot(r1:r2,getBaseCoverage(bm_hct116_1,r1,r2,'binWidth',1),'b'); % plot high-resolution coverage of bm_hct116_2 h2 = plot(r1:r2,getBaseCoverage(bm_hct116_2,r1,r2,'binWidth',1),'g'); % mark the CpG islands within the [r1 r2] region for i = 1:numel(cpgi.Starts) if cpgi.Starts(i)>r1 && cpgi.Stops(i)<r2 % is CpG island inside [r1 r2]? px = [cpgi.Starts([i i]) cpgi.Stops([i i])]; % x-coordinates for patch py = [0 max(ylim) max(ylim) 0]; % y-coordinates for patch hp = patch(px,py,'r','FaceAlpha',.1,'EdgeColor','r','Tag','cpgi'); end end % mark the exons at the bottom of the axes for i = 1:numel(transcripts) exons = getSubset(barx1,'Transcript',transcripts{i},'Feature','exon'); for j = 1:exons.NumEntries px = [exons.Start([j j]);exons.Stop([j j])]'; % x-coordinates for patch py = [0 1 1 0]-i*2-1; % y-coordinates for patch hq = patch(px,py,'b','FaceAlpha',.1,'EdgeColor','b','Tag','exon'); end end axis([r1 r2 -numel(transcripts)*2-2 80]) % zooms-in the y-axis fixGenomicPositionLabels(gca) % formats tick labels and adds datacursors ylabel('Coverage') xlabel('Chromosome 9 position') title('High resolution coverage in the BARX1 gene') legend([h1 h2 hp hq],'HCT116-1','HCT116-2','CpG Islands','Exons','Location','NorthWest')

Observe the highly methylated region in the 5' promoter region (right-most CpG island). Recall that for this gene transcription occurs in the reverse strand. More interesting, observe the highly methylated regions that overlap the initiation of each of the two annotated transcripts (two middle CpG islands).
Differential Analysis of Methylation Patterns
In the study by Serre et al. another cell line is also analyzed. New cells (DICERex5) are derived from the same HCT116 colon cancer cells after truncating the DICER1 alleles. It has been reported in literature [5] that there is a localized change of DNA methylation at small number of gene promoters. In this example, you will find significant 100-bp windows in two sample replicates of the DICERex5 cells following the same approach as the parental HCT116 cells, and then you will search statistically significant differences between the two cell lines.
The helper function getWindowCounts captures the similar steps to find windows with significant coverage as before. getWindowCounts returns vectors with counts, p-values, and false discovery rates for each new replicate.
bm_dicer_1 = BioMap('SRR030222.bam','SelectRef','gi|224589821|ref|NC_000009.11|'); bm_dicer_2 = BioMap('SRR030223.bam','SelectRef','gi|224589821|ref|NC_000009.11|'); [counts_3,pval3,fdr3] = getWindowCounts(bm_dicer_1,4,w,100); [counts_4,pval4,fdr4] = getWindowCounts(bm_dicer_2,4,w,100); w3 = fdr3<.01; % logical vector indicating significant windows in DICERex5_1 w4 = fdr4<.01; % logical vector indicating significant windows in DICERex5-2 w34 = w3 & w4; % logical vector indicating significant windows in both replicates Number_of_sig_windows_DICERex5_1 = sum(w3) Number_of_sig_windows_DICERex5_2 = sum(w4) Number_of_sig_windows_DICERex5 = sum(w34)
Number_of_sig_windows_DICERex5_1 =
908
Number_of_sig_windows_DICERex5_2 =
1041
Number_of_sig_windows_DICERex5 =
759
To perform a differential analysis you use the 100-bp windows that are significant in at least one of the samples (either HCT116 or DICERex5).
wd = w34 | w12; % logical vector indicating windows included in the diff. analysis counts = [counts_1(wd) counts_2(wd) counts_3(wd) counts_4(wd)]; ws = w(wd); % window start for each row in counts
Use the function manorm to normalize the data. The PERCENTILE name-value pair lets you filter out windows with very large number of counts while normalizing, since these windows are mainly due to artifacts, such as repetitive regions in the reference chromosome.
counts_norm = round(manorm(counts,'percentile',90).*100);
Use the function mattest to perform a two-sample t-test to identify differentially covered windows from the two different cell lines.
pval = mattest(counts_norm(:,[1 2]),counts_norm(:,[3 4]),'bootstrap',true,... 'showhist',true,'showplot',true);
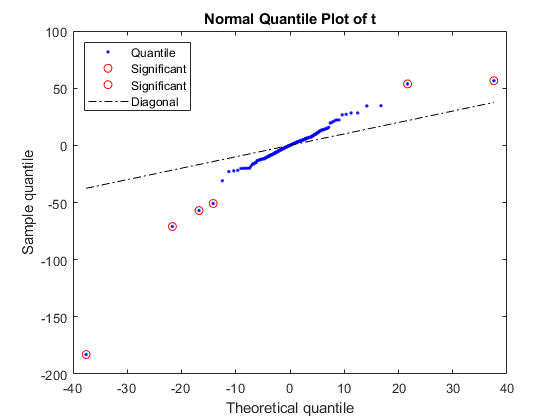
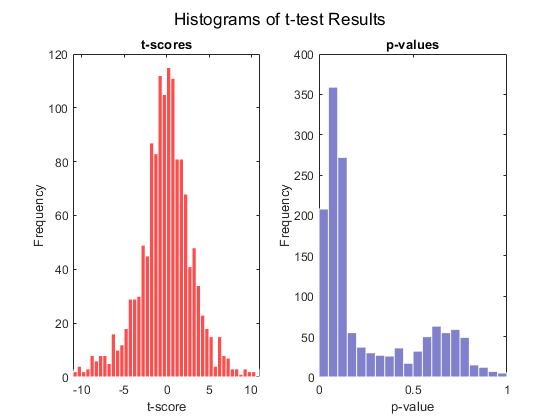
Create a report with the 25 most significant differentially covered windows. While creating the report use the helper function findClosestGene to determine if the window is intergenic, intragenic, or if it is in a proximal promoter region.
[~,ord] = sort(pval); fprintf('Window Pos Type p-value HCT116 DICERex5\n\n'); for i = 1:25 j = ord(i); [~,msg] = findClosestGene(a9,[ws(j) ws(j)+99]); fprintf('%10d %-25s %7.6f%5d%5d %5d%5d\n', ... ws(j),msg,pval(j),counts_norm(j,:)); end
Window Pos Type p-value HCT116 DICERex5
140311701 Intergenic (EXD3) 0.000020 13 13 104 105
139546501 Intragenic 0.001525 21 21 91 93
10901 Intragenic 0.002222 258 257 434 428
120176801 Intergenic (ASTN2) 0.002270 266 270 155 155
139914801 Intergenic (ABCA2) 0.002482 64 63 26 25
126128501 Intergenic (CRB2) 0.002664 94 93 129 130
71939501 Prox. Promoter (FAM189A2) 0.004687 107 101 0 0
124461001 Intergenic (DAB2IP) 0.004747 77 76 39 37
140086501 Intergenic (TPRN) 0.005489 47 42 123 124
79637201 Intragenic 0.006323 52 51 32 31
136470801 Intragenic 0.006323 52 51 32 31
140918001 Intergenic (CACNA1B) 0.006786 176 169 71 68
100615901 Intergenic (FOXE1) 0.006969 262 253 123 118
98221901 Intergenic (PTCH1) 0.008291 26 30 104 99
138730601 Intergenic (CAMSAP1) 0.008602 26 21 97 93
89561701 Intergenic (GAS1) 0.008653 77 76 6 12
977401 Intergenic (DMRT3) 0.008678 236 245 129 124
37002601 Intergenic (PAX5) 0.008822 133 127 207 211
139744401 Intergenic (PHPT1) 0.009078 47 46 32 31
126771301 Intragenic 0.009547 43 46 97 93
93922501 Intragenic 0.009565 34 34 149 161
94187101 Intragenic 0.009579 73 80 6 6
136044401 Intragenic 0.009623 39 34 110 105
139611201 Intergenic (FAM69B) 0.009623 39 34 110 105
139716201 Intergenic (C9orf86) 0.009860 73 72 136 130
Plot the DNA methylation profile for the promoter region of gene FAM189A2, the most significant differentially covered promoter region from the previous list. Overlay the CpG islands and the FAM189A2 gene.
range = getRange(getSubset(a9,'Feature','FAM189A2')); r1 = range(1)-1000; r2 = range(2)+1000; figure hold on % plot high-resolution coverage of all replicates h1 = plot(r1:r2,getBaseCoverage(bm_hct116_1,r1,r2,'binWidth',1),'b'); h2 = plot(r1:r2,getBaseCoverage(bm_hct116_2,r1,r2,'binWidth',1),'g'); h3 = plot(r1:r2,getBaseCoverage(bm_dicer_1,r1,r2,'binWidth',1),'r'); h4 = plot(r1:r2,getBaseCoverage(bm_dicer_2,r1,r2,'binWidth',1),'m'); % mark the CpG islands within the [r1 r2] region for i = 1:numel(cpgi.Starts) if cpgi.Starts(i)>r1 && cpgi.Stops(i)<r2 % is CpG island inside [r1 r2]? px = [cpgi.Starts([i i]) cpgi.Stops([i i])]; % x-coordinates for patch py = [0 max(ylim) max(ylim) 0]; % y-coordinates for patch hp = patch(px,py,'r','FaceAlpha',.1,'EdgeColor','r','Tag','cpgi'); end end % mark the gene at the bottom of the axes px = range([1 1 2 2]); py = [0 1 1 0]-2; hq = patch(px,py,'b','FaceAlpha',.1,'EdgeColor','b','Tag','gene'); axis([r1 r1+4000 -4 30]) % zooms-in fixGenomicPositionLabels(gca) % formats tick labels and adds datacursors ylabel('Coverage') xlabel('Chromosome 9 position') title('DNA Methylation profiles along the promoter region of the FAM189A2 gene') legend([h1 h2 h3 h4 hp hq],... 'HCT116-1','HCT116-2','DICERex5-1','DICERex5-2','CpG Islands','FAM189A2 Gene',... 'Location','NorthEast')

Observe that the CpG islands are clearly unmethylated for both of the DICERex5 replicates.
References
[1] Serre, D., Lee, B.H., and Ting A.H., "MBD-isolated Genome Sequencing provides a high-throughput and comprehensive survey of DNA methylation in the human genome", Nucleic Acids Research, 38(2):391-9, 2010.
[2] Langmead, B., Trapnell, C., Pop, M., and Salzberg, S.L., "Ultrafast and Memory-efficient Alignment of Short DNA Sequences to the Human Genome", Genome Biology, 10(3):R25, 2009.
[3] Li, H., et al., "The Sequence Alignment/map (SAM) Format and SAMtools", Bioinformatics, 25(16):2078-9, 2009.
[4] Gardiner-Garden, M. and Frommer, M., "CpG islands in vertebrate genomes", Journal of Molecular Biology, 196(2):261-82, 1987.
[5] Ting, A.H., et al., "A Requirement for DICER to Maintain Full Promoter CpG Island Hypermethylation in Human Cancer Cells", Cancer Research, 68(8):2570-5, 2008.
[6] Benjamini, Y. and Hochberg, Y., "Controlling the false discovery rate: a practical and powerful approach to multiple testing", Journal of the Royal Statistical Society, 57(1):289-300, 1995.