Number of Recursions

Number of call graph cycles over one or more functions

Description

The metric provides a quantitative estimate of the number of recursion cycles in your project. The metric is the sum of:

Number of direct recursions (self recursive functions or functions calling themselves).
Number of strongly connected components formed by the indirect recursion cycles in your project. If you consider the recursion cycles as a directed graph, the graph is strongly connected if there is a path between all pairs of vertices.
To compute the number of strongly connected components:
1. Draw the recursion cycles in your code.
  For instance, the recursion cycles in this example are shown below.
```
volatile int checkStatus;
void func1() {
   if(checkStatus) {
        func2();
   }
   else {
        func3();
   }
}

func2() {
   func1();
}

func3() {
   func1();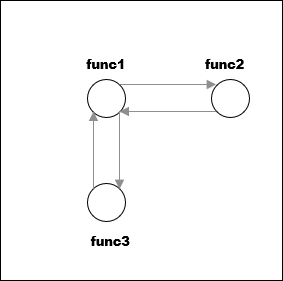
}
```
2. Identify the number of strongly connected components formed by the recursion cycles.
  In the preceding example, there is one strongly connected component. You can move from any vertex to another vertex by following the paths in the graph.
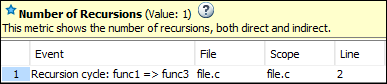
  The event list below the metric shows one of the recursion cycles in the strongly connected component.

Polyspace^® computes this metric using a syntactical call hierarchy, which is different than the call hierarchy computed by Polyspace. Because this metric is calculated using a syntactical hierarchy, it considers calls in unreachable branches and does not consider calls through function pointers.

The recommended upper limit for this metric is 0. To avoid the possibility of exceeding available stack space, do not use recursions in your code. Recursions can tend to exhaust stack space easily. See examples of stack size growth with recursions described for this CERT-C rule that forbids recursions.

To detect use of recursions, check for violations of one of MISRA C:2012 Rule 17.2,MISRA C™: 2004 Rule 16.2, MISRA C++:2008 Rule 7-5-4 , JSF^® Rule 119, or Number of Recursions Exceeds Threshold. Note that:

The rule checkers report each function that calls itself, directly or indirectly. Even if several functions are involved in one recursion cycle, each function is individually reported.
The rule checkers consider explicit function calls only. For instance, in C++ code, the rule checkers ignore implicit calls to constructors during object creation. However, the metrics computation considers both implicit and explicit calls.

To enforce limits on metrics, see:

Examples

expand all

Direct Recursion

int getVal(void);
int sum(int val) {
    if(val<0)
        return 0;
    else
        return (val + sum(val-1));
}

void main() {
    int count = getVal(), total;
    assert(count > 0 && count <100);
    total = sum(count);
}

In this example, the number of recursions is 1.

A direct recursion is a recursion where a function calls itself in its own body. For direct recursions, the number of recursions is equal to the number of recursive functions.

Indirect Recursion with One Call Graph Cycle

volatile int signal;
void operation2(void);

void operation1(void) {
    int stop = signal%2;
    if(!stop)
        operation2();
}

void operation2(void) {
    operation1();
}

void main() {
    operation1();
}

In this example, the number of recursions is one. The two functions operation1 and operation2 are involved in the call graph cycle operation1 → operation2 → operation1.

An indirect function is a recursion where a function calls itself through other functions. For indirect recursions, the number of recursions can be different from the number of recursive functions.

Multiple Call Graph Cycles Forming One Strongly Connected Component


volatile int checkStatus;
void func1() {
   if(checkStatus) {
        func2();
   }
   else {
        func3();
   }
}

func2() {
   func1();
}

func3() {
   func1();
}

In this example, there are two call graph cycles:

func1 → func2 → func1
func1 → func3 → func1

However, the cycles form one strongly connected component. You can move from any vertex to another vertex by following the paths in the graph. Hence, the number of recursions is one.

Indirect Recursion with Two Call Graph Cycles

volatile int signal;
void operation1_1();
void operation2_1();

void operation1() {
    int stop = signal%2;
    if(!stop)
        operation1_1();
}


void operation1_1() {
    operation1();
}

void operation2() {
    int stop = signal%2;
    if(!stop)
        operation2_1();
}

void operation2_1() {
    operation2();
}

void main(){
    operation1();
    operation2();
}

In this example, the number of recursions is two.

There are two call graph cycles:

operation1 → operation1_1 → operation1
operation2 → operation2_1 → operation2

The call graph cycles form two strongly connected components.

Same Function Called in Direct and Indirect Recursion

volatile int signal;
void operation2();

void operation1() {
    int stop = signal%3;
    if(stop==1)
        operation1();
    else if(stop==2)
        operation2();
}

void operation2() {
    operation1();
}

void main() {
    operation1();
}

In this example, the number of recursions is two: