BER Simulations with Parallel Computing Toolbox

This example uses:

This example shows how to improve the execution speed of communication systems involving BER simulations. To improve the performance of these systems, one of the available options is to parallelize the simulations. This example introduces the usage of the Parallel Computing Toolbox™ in BER simulations. It presents two possible ways of parallelizing BER simulations and recommends the better method.

License Check and Opening a Parallel Pool

This section checks for the availability of Parallel Computing Toolbox. If available, it opens a parallel pool of workers and assigns the maximum number of available workers in the pool to the variable numWorkers. If not available it assigns numWorkers = 1, in which case the example runs on a single core.

[licensePCT,~] = license( 'checkout','Distrib_Computing_Toolbox');
if ( licensePCT && ~isempty(ver('parallel')))
    if isempty(gcp('nocreate'))
        parpool;
    end
    pool = gcp;
    numWorkers = pool.NumWorkers;
else
    numWorkers = 1;
end

Starting parallel pool (parpool) using the 'local' profile ...
Connected to the parallel pool (number of workers: 6).

Initialization

This example parallelizes the Spatial Multiplexing example to demonstrate the usage of Parallel Computing Toolbox. The following are the parameters needed to simulate this example.

EbNo = 1:2:11;  % Eb/No in dB
N = 2;          % Number of transmit antennas
M = 2;          % Number of receive antennas
modOrd = 2;     % constellation size = 2^modOrd
numBits = 1e6;  % Number of bits
numErrs =  100; % Number of errors
lenEbNo = length(EbNo);
% Create a local random stream to be used for data generation for
% repeatability. Use the combined multiple recursive generator since it
% supports substreams.
hStr = RandStream('mrg32k3a'); % Setting the random stream
[berZF,berMMSE] = deal(zeros(lenEbNo,3));
[nerrsZF,nbitsZF,nerrsMMSE,nbitsMMSE] = deal(zeros(numWorkers,lenEbNo));

Parallelizing Across the Eb/No Range

The first method parallelizes across the Eb/No range, where one worker processes a single Eb/No value. Here the performance is limited by the time required to process the highest Eb/No value.

simIndex = 1;
str = 'Across the Eb/No range';
disp('Performing BER simulations with one worker processing one Eb/No value ...');

Performing BER simulations with one worker processing one Eb/No value ...

tic
parfor idx = 1:lenEbNo
    [BER_ZF,BER_MMSE] = simBERwithPCT(N,M,EbNo,modOrd, ...
        idx,hStr,numBits,numErrs);
    berZF(idx,:) = BER_ZF(idx,:);
    berMMSE(idx,:) = BER_MMSE(idx,:);
end
timeRange = toc;
clockBERwithPCT(simIndex,timeRange,timeRange,str);

Parallelizing Across the Number of Workers in the Parallel Pool

The second method parallelizes across the number of available workers, where each worker processes the full Eb/No range. However, each worker counts (total errors/numWorkers) errors before proceeding to the next Eb/No value. This method uses all available cores equally efficiently.

simIndex = simIndex + 1;
str = 'Across the number of available workers';
seed = 0:numWorkers-1;
disp('Performing BER simulations with each worker processing the entire range ...');

Performing BER simulations with each worker processing the entire range ...

tic
parfor n = 1:numWorkers
    hStr = RandStream('mrg32k3a','Seed',seed(n));
    for idx = 1:lenEbNo
        [BER_ZF,BER_MMSE] = simBERwithPCT(N,M,EbNo,modOrd, ...
            idx,hStr,numBits/numWorkers,numErrs/numWorkers);
        nerrsZF(n,idx) = BER_ZF( idx,2);
        nbitsZF(n,idx) = BER_ZF( idx,3);
        nerrsMMSE(n,idx) = BER_MMSE(idx,2);
        nbitsMMSE(n,idx) = BER_MMSE(idx,3);
    end
end
bZF = sum(nerrsZF,1)./sum(nbitsZF,1);
bMMSE = sum(nerrsMMSE,1)./sum(nbitsMMSE,1);
timeWorker = toc;

Below are the results obtained on a Windows® 7, 64-bit, Intel® Xeon® CPU W3550, ~3.1GHz, 12.288GB RAM machine using four cores. The table shows the performance comparison of the above methods. We see that the second method performs better than the first. These are the results obtained on a single run and may vary from run to run.

--------------------------------------------------------------------------------------------
Type of Parallelization                             | Elapsed Time (sec)| Speedup Ratio
1. Across the Eb/No range                           |           89.7366 |       1.0000
2. Across the number of available workers           |           28.4443 |       3.1548
--------------------------------------------------------------------------------------------

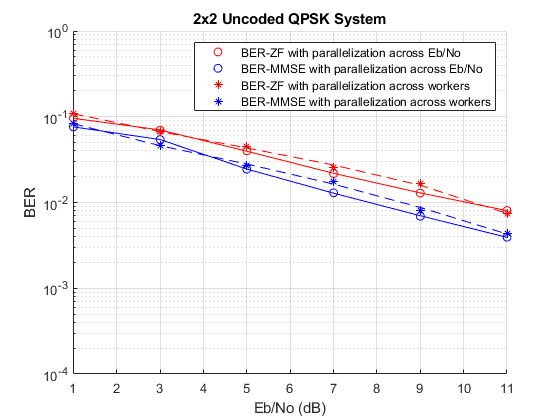
The plot below shows the BER curves obtained for the zero forcing (ZF) and minimum mean squared error (MMSE) receivers using the different parallelization methods.

plotBERwithPCT(EbNo,berZF(:,1),berMMSE(:,1),bZF,bMMSE);

To generate a performance comparison table for your machine, uncomment the following line of code and run this entire script.

% clockBERwithPCT(simIndex,timeRange,timeWorker,str);

Appendix

The following functions are used in this example: