Log-Likelihood Ratio (LLR) Demodulation

Initialization

Initialize simulation parameters.

M = 4;               % Modulation order
bitsPerIter = 1.2e4; % Number of bits to simulate
EbNo = 3;            % Information bit Eb/No in dB

Initialize coding properties for a rate 1/2, constraint length 7 code.

codeRate = 1/2;          % Code rate of convolutional encoder
constLen = 7;            % Constraint length of encoder
codeGenPoly = [171 133]; % Code generator polynomial of encoder
tblen = 32;              % Traceback depth of Viterbi decoder
trellis = poly2trellis(constLen,codeGenPoly);

Create a comm.ConvolutionalEncoder System object™ by using trellis as an input.

enc = comm.ConvolutionalEncoder(trellis);

Channel

The signal going into the AWGN channel is the modulated encoded signal. To achieve the required noise level, adjust the Eb/No for coded bits and multi-bit symbols. Calculate the $$SNR$$ value based on the $$E_b/N_o$$ value you want to simulate.

SNR = convertSNR(EbNo,"ebno","BitsPerSymbol",log2(M),"CodingRate",codeRate);

Viterbi Decoding

Create comm.ViterbiDecoder objects to act as the hard-decision, unquantized, and soft-decision decoders. For all three decoders, set the traceback depth to tblen.

decHard = comm.ViterbiDecoder(trellis,'InputFormat','Hard', ...
    'TracebackDepth',tblen);

decUnquant = comm.ViterbiDecoder(trellis,'InputFormat','Unquantized', ...
    'TracebackDepth',tblen);

decSoft = comm.ViterbiDecoder(trellis,'InputFormat','Soft', ...
    'SoftInputWordLength',3,'TracebackDepth',tblen);

Calculating the Error Rate

Create comm.ErrorRate objects to compare the decoded bits to the original transmitted bits. The Viterbi decoder creates a delay in the decoded bit stream output equal to the traceback length. To account for this delay, set the ReceiveDelay property of the comm.ErrorRate objects to tblen.

errHard = comm.ErrorRate('ReceiveDelay',tblen);
errUnquant = comm.ErrorRate('ReceiveDelay',tblen);
errSoft = comm.ErrorRate('ReceiveDelay',tblen);

System Simulation

Generate bitsPerIter message bits. Then convolutionally encode and modulate the data.

txData = randi([0 1],bitsPerIter,1); 
encData = enc(txData);
modData = pskmod(encData,M,pi/4,InputType="bit");

Pass the modulated signal through an AWGN channel.

[rxSig,nVar] = awgn(modData,SNR);

Before using a comm.ViterbiDecoder object in the soft-decision mode, the output of the demodulator needs to be quantized. This example uses a comm.ViterbiDecoder object with a SoftInputWordLength of 3. This value is a good compromise between short word lengths and a small BER penalty. Define partition points for 3-bit quantization.

demodLLR.Variance = nVar;
partitionPoints = (-1.5:0.5:1.5)/nVar;

Demodulate the received signal and output hard-decision bits.

hardData = pskdemod(rxSig,M,pi/4,OutputType="bit");

Demodulate the received signal and output LLR values.

LLRData = pskdemod(rxSig,M,pi/4,OutputType="llr",NoiseVariance=nVar);

Hard-decision decoding

Pass the demodulated data through the Viterbi decoder. Compute the error statistics.

rxDataHard = decHard(hardData);
berHard = errHard(txData,rxDataHard);

Unquantized decoding

Pass the demodulated data through the Viterbi decoder. Compute the error statistics.

rxDataUnquant = decUnquant(LLRData);
berUnquant = errUnquant(txData,rxDataUnquant);

Soft-decision decoding

Pass the demodulated data to the quantiz function. This data must be multiplied by -1 before being passed to the quantizer, because, in soft-decision mode, the Viterbi decoder assumes that positive numbers correspond to 1s and negative numbers to 0s. Pass the quantizer output to the Viterbi decoder. Compute the error statistics.

quantizedValue = quantiz(-LLRData,partitionPoints);
rxDataSoft = decSoft(double(quantizedValue));
berSoft = errSoft(txData,rxDataSoft);

Running Simulation Example

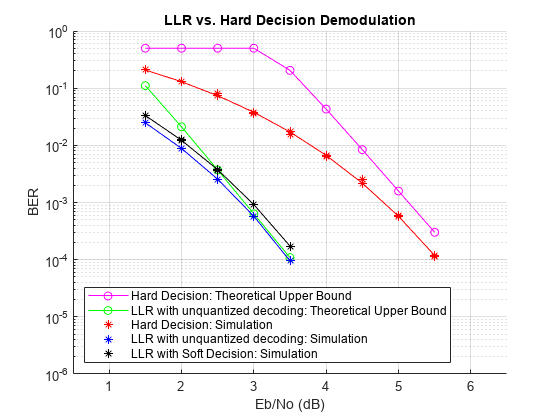
Simulate the previously described communications system over a range of Eb/No values by executing the simulation file simLLRvsHD. It plots BER results as they are generated. BER results for hard-decision demodulation and LLR demodulation with unquantized and soft-decision decoding are plotted in red, blue, and black, respectively. A comparison of simulation results with theoretical results is also shown. Observe that the BER is only slightly degraded by using soft-decision decoding instead of unquantized decoding. The gap between the BER curves for soft-decision decoding and the theoretical bound can be narrowed by increasing the number of quantizer levels.

This example may take some time to compute BER results. If you have the Parallel Computing Toolbox™ (PCT) installed, you can set usePCT to true to run the simulation in parallel. In this case, the file LLRvsHDwithPCT is run.

To obtain results over a larger range of Eb/No values, modify the appropriate supporting files. Note that you can obtain more statistically reliable results by collecting more errors.

usePCT = false;
if usePCT && license('checkout','Distrib_Computing_Toolbox') ...
        && ~isempty(ver('parallel'))
    LLRvsHDwithPCT(1.5:0.5:5.5,5);
else
    simLLRvsHD(1.5:0.5:5.5,5);
end

Appendix

The following functions are used in this example: