Parallel Concatenated Convolutional Coding: Turbo Codes
This example characterizes the performance of turbo codes over a noisy channel. It shows the basic structure of turbo codes at the transmitter and receiver. We chose the Long Term Evolution (LTE) specifications [ 4 ] for the constituent component parameters.
The invention of turbo codes [ 1 ], along with the development of iterative decoding principles with near Shannon limit performance, has led to their absorption in a wide variety of applications some of which include deep space communications, third generation wireless standards, and digital video broadcasting [ 3 ].
Available Example Implementations
This example includes both MATLAB® and Simulink® implementations:
MATLAB script using System objects: commTurboCoding.m
Simulink model using System blocks: commpccc.slx
Simulink model using variable-sized code-blocks: commpcccvs.slx
Both the MATLAB and Simulink implementations of the system are set up so you can simulate the system over a range of Eb/No values for user-specified system parameters like code block length and number of decoding iterations. The following sections use the fixed-size code-block Simulink implementation to describe the details of the coding scheme.
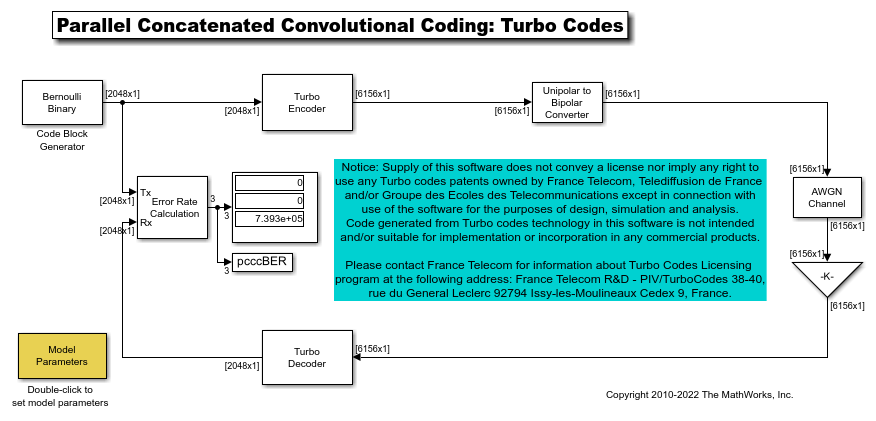
Turbo Encoder
A comm.TurboEncoder is a parallel concatenation scheme with multiple constituent Convolutional encoders. The first encoder operates directly on the input bit sequence, while any others operate on interleaved input sequences, obtained by interleaving the input bits over a block length.
The System block based Turbo Encoder block uses two identical 8-state recursive systematic convolutional encoders. The comm.ConvolutionalEncoder System object™ uses the "Terminated" setting for the TerminationMethod property. This restores the encoders to the starting all-zeros state for each frame of data the block processes. The internal block interleaver uses pre-computed permutation indices, based on the user-specified Code block length parameter (see the Model Parameters block ). The bit reordering subsystem removes the extra set of systematic bits from the second encoder output and realizes the trellis termination as per [ 4 ].
Iterative Decoding
For iterative decoding of the parallel concatenated encoding scheme, the comm.TurboDecoder uses the a posteriori probability (APP) decoder [ 2 ] as the constituent decoder component.
Each comm.APPDecoder System object corresponds to a constituent encoder which provides an updated sequence of log-likelihood values for the uncoded bits from the received sequence of log-likelihoods for the channel (coded) bits. For each set of received channel sequences, the decoder iteratively updates the log-likelihoods for the uncoded bits until a stopping criterion is met. This example uses a fixed number of decoding iterations, as specified by the Number of decoding iterations parameter in the model's Model Parameters block. The default number of iterations is six.
The TerminationMethod property for the APP Decoder System object is set to be "Terminated" to match the encoders. The decoder does not assume knowledge of the tail bits and as a result, these are excluded from the multiple iterations.
The internal interleaver of the decoder is identical to the one the encoder uses. It reorders the sequences so that they are properly aligned at the two decoders.
BER Performance
The following figure shows the bit error rate performance of the parallel concatenated coding scheme in an AWGN channel over a range of Eb/No values for two sets of code block lengths and number of decoding iterations.
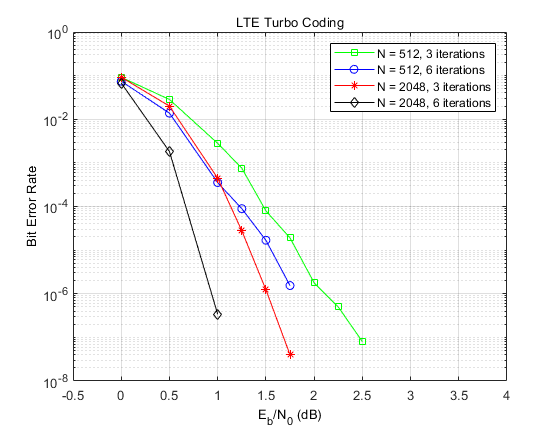
As the figure shows, the iterative decoding performance improves with an increase in the number of decoding iterations (at the expense of computational complexity) and larger block lengths (at the expense of decoding latency).
Variable-Sized Turbo Coding
The companion model TurboCodingSimulinkExample.m highlights turbo coding using variable-sized code-blocks within a simulation run.

The model is set up to run two user specified code-block lengths, which vary as per the selected control signal. The interleaver indices per block length and the noise variance are calculated per time step. Using the CRC syndrome detector, the model displays the code-block error rate in addition to the bit error rate, as the former is the more relevant performance metric with variable-sized code blocks.
CBER Performance
The following figure shows the code-block error rate performance of the parallel concatenated coding scheme in an AWGN channel over a range of Eb/No values for a similar set up as used for BER.
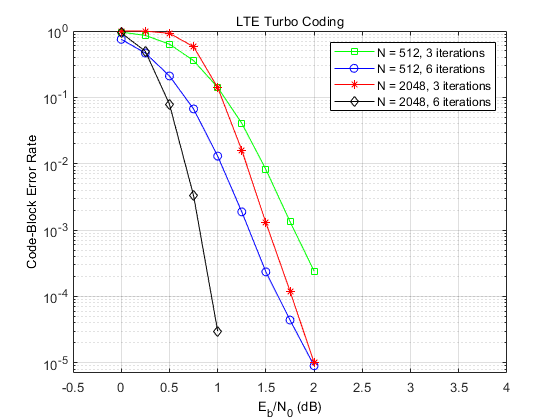
We observe similar improvements as before in performance with increase in the number of decoding iterations and/or block lengths.
Further Exploration
The example allows you to explore the effects of different block lengths and number of decoding iterations on the system performance. It supports all of the 188 code block sizes specified in [ 4 ] for a user-specified fixed number of decoding iterations.
Selected References
C. Berrou, A. Glavieux and P. Thitimajshima, "Near Shannon limit error correcting coding and decoding: turbo codes," Proc. IEEE® Int. Conf. on Communications, Geneva, Switzerland, May 1993, pp. 1064-1070.
Benedetto, S., G. Montorsi, D. Divsalar, and F. Pollara, "A Soft-Input Soft-Output Maximum A Posterior (MAP) Module to Decode Parallel and Serial Concatenated Codes," JPL TDA Progress Report, Vol. 42-127, Nov. 1996.
Schlegel, Christian B. and Lance C. Perez, "Trellis and Turbo Coding", IEEE Press, 2004.
3GPP TS 36.212 v10.8.0, "3rd Generation partnership project; Technical specification group radio access network; Evolved Universal Terrestrial Radio Access (E-UTRA); Multiplexing and channel coding (Release 10)", 2013-06.