Accelerate Simulation Using GPUs
You can design your MATLAB® simulation by using functions or System objects that support GPU-based processing. You can also build your Simulink® model by using MATLAB System (Simulink) blocks that include GPU-based System objects in them. GPUs excel at processing large quantities of data and performing computations with high compute intensity. Processing large quantities of data is one way to maximize the throughput of your GPU in a simulation. The amount of data that the GPU processes at any one time depends on the size of the data passed to the input of a GPU-based simulation.
Passing MATLAB arrays to a GPU-based simulation requires transferring the initial data
from a CPU to the GPU for GPU-based processing. Afterward, the simulation transfers the
output data back to the CPU. Repeating this process introduces latency. Passing data in
the form of a gpuArray (Parallel Computing Toolbox) object to a GPU-capable
function or System object™ avoids latency from data transfer. Therefore, a GPU-based simulation runs
faster when you supply a gpuArray object as the input and minimize the
number of data transfers between the CPU and the GPU in your simulation. For more
information, see Establish Arrays on a GPU (Parallel Computing Toolbox).
LDPC Decoding Using GPU
Use a GPU to accelerate LDPC encoding, PSK modulation, AWGN channel modeling, PSK demodulation, LDPC decoding, and bit error rate computation. In this example you compute the error statistics for the belief propagation decoding algorithm and the normalized min-sum decoding algorithm.
Create LDPC Configuration Objects
Create an LDPC encoder configuration object and an LDPC decoder configuration object. Define simulation variables.
% Use ldpcQuasiCyclicMatrix to create a parity-check matrix load("LDPCExamplePrototypeMatrix.mat","P"); % A prototype matrix from the 5G standard blockSize = 384; H = ldpcQuasiCyclicMatrix(blockSize, P); encoderCfg = ldpcEncoderConfig(H); decoderCfg1 = ldpcDecoderConfig(encoderCfg); % The default algorithm is "bp" decoderCfg2 = ldpcDecoderConfig(encoderCfg,"norm-min-sum"); M = 4; % Modulation order (QPSK) snr = [-2 -1.5 -1]; numFramesPerCall = 50; numCalls = 40; maxNumIter = 20; s = rng(1235); % Fix random seed errRate = zeros(length(snr),2);
Compute Bit Error Rates
Generate random bits in a gpuArray (Parallel Computing Toolbox) object and let its data flow through the ldpcEncode, pskmod, awgn, pskdemod, ldpcDecode, and biterr functions. For each SNR setting, compute the error statistics for the belief propagation decoding algorithm and the normalized min-sum decoding algorithm.
for ii = 1:length(snr) ttlErr = [0 0]; noiseVariance = 1/10^(snr(ii)/10); for counter = 1:numCalls data = gpuArray.randi([0 1],encoderCfg.NumInformationBits,numFramesPerCall,'logical'); % Transmit and receive LDPC coded signal data encData = ldpcEncode(data,encoderCfg); modSig = pskmod(encData,M,pi/4,'InputType','bit'); rxSig = awgn(modSig,snr(ii)); % Signal power = 0 dBW demodSig = pskdemod(rxSig,M,pi/4,... 'OutputType','approxllr','NoiseVariance',noiseVariance); % Decode and update number of bit errors % Using bp rxBits1 = ldpcDecode(demodSig,decoderCfg1,maxNumIter); numErr1 = biterr(data,rxBits1); % Using norm-min-sum rxBits2 = ldpcDecode(demodSig,decoderCfg2,maxNumIter); numErr2 = biterr(data,rxBits2); ttlErr = ttlErr + [numErr1 numErr2]; end ttlBits = numCalls*numel(rxBits1); errRate(ii,:) = ttlErr/ttlBits; end
Compare Bit Error Rates
Plot the error statistics. The belief propagation algorithm is expected to achieve a slightly lower bit error rate than the normalized min-sum algorithm.
plot(snr,errRate,'-x') grid on legend('bp','norm-min-sum') xlabel('SNR (dB)') ylabel('BER')
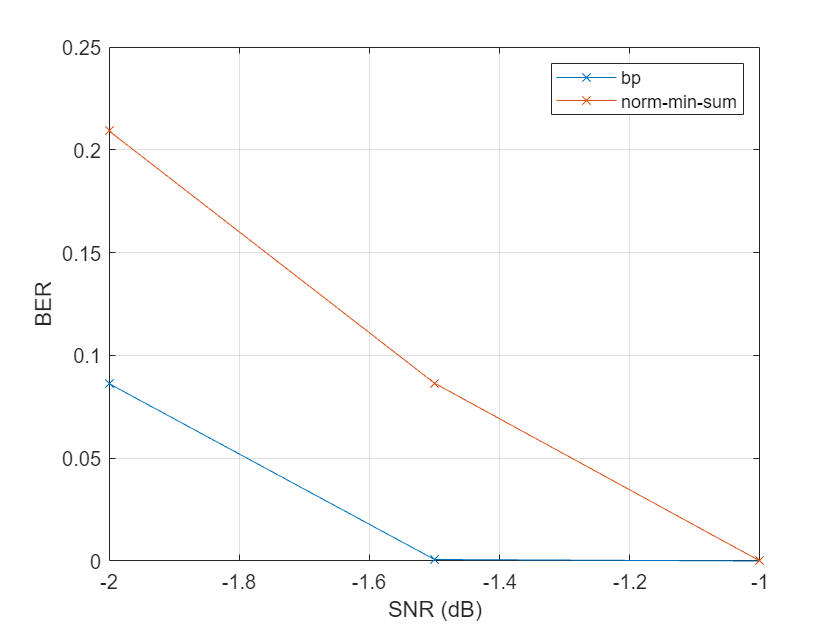
Compare Speeds
Compare the execution speeds of four cases. By default, ldpcDecode terminates decoding when all parity checks are satisfied.
% Use belief propagation algorithm on CPU, without multithreading demodSigCPU = gather(demodSig); tic [rxBitsCPU1,actualNumIterCPU1,finalParityChecksCPU1] = ... ldpcDecode(demodSigCPU,decoderCfg1,maxNumIter,'Multithreaded',false); toc
Elapsed time is 4.270400 seconds.
% Use belief propagation algorithm on CPU, with multithreading tic [rxBitsCPU2,actualNumIterCPU2,finalParityChecksCPU2] = ... ldpcDecode(demodSigCPU,decoderCfg1,maxNumIter); toc
Elapsed time is 1.069500 seconds.
% Use belief propagation algorithm on GPU tic [rxBits1,actualNumIter1,finalParityChecks1] = ... ldpcDecode(demodSig,decoderCfg1,maxNumIter); toc
Elapsed time is 2.117112 seconds.
% Use normalized min-sum algorithm on GPU tic [rxBits2,actualNumIter2,finalParityChecks2] = ... ldpcDecode(demodSig,decoderCfg2,maxNumIter); toc
Elapsed time is 0.615488 seconds.
Examine Optional Decoder Outputs
Confirm that the normalized min-sum algorithm needs fewer iterations than the belief propagation algorithm when the SNR is sufficiently high.
length(find(actualNumIter2 < actualNumIter1))
ans = 50
length(find(actualNumIter2 == actualNumIter1))
ans = 0
Confirm that the final parity checks are all zeros when the actual number of iterations executed is less than the maximum number of iterations specified.
nnz(finalParityChecks1(:,actualNumIter1<maxNumIter))
ans = 0
nnz(finalParityChecks2(:,actualNumIter2<maxNumIter))
ans = 0
Restore the state for random number generation.
rng(s);
Process Multiple Data Frames Using GPU-Based System Objects
You can use a single GPU System object™ to process multiple data frames simultaneously. Some GPU-based System objects, such as the Viterbi decoder, the frame size of your system cannot be inferred from an object property. Instead, you must define the number of frames present in the input data by using the NumFrames property of the Viterbi decoder object.
numframes = 10; convEncoder = comm.ConvolutionalEncoder( ... TerminationMethod="Terminated"); vitDecoder = comm.ViterbiDecoder( ... TerminationMethod="Terminated");
Create a GPU-based Viterbi decoder System object using the NumFrames property.
vitGPUDecoder = comm.gpu.ViterbiDecoder( ... TerminationMethod="Terminated", ... NumFrames=numframes); msg = randi([0 1],200,numframes); for ii=1:numframes convEncOut(:,ii) = 1-2*convEncoder(msg(:,ii)); end % Decode on the CPU for ii=1:numframes cVitOut(:,ii) = vitDecoder(convEncOut(:,ii)); end % Decode on the GPU gVitOut = vitGPUDecoder(convEncOut(:)); % Check equality isequal(gVitOut,cVitOut(:))
ans = logical
1
Pass Data to GPU-Based System Objects Using gpuarray Input
In this example, you transmit 1/2 rate convolutionally encoded 16-PSK-modulated data through an AWGN channel, demodulate and decode the received data, and assess the error rate of the received data. For this implementation, you use the GPU-based Viterbi decoder System object™ to process multiple signal frames in a single call and then use gpuArray (Parallel Computing Toolbox) objects to pass data into and out of the GPU-based System objects.
Create GPU-based System objects for PSK modulation and demodulation, convolutional encoding, and Viterbi decoding. Create a System object for error rate calculation.
M = 16; % Modulation order numframes = 100; gpuconvenc = comm.gpu.ConvolutionalEncoder; gpupskmod = comm.gpu.PSKModulator(M,pi/16,BitInput=true); gpupskdemod = comm.gpu.PSKDemodulator(M,pi/16,BitOutput=true); gpuvitdec = comm.gpu.ViterbiDecoder( ... InputFormat='Hard', ... TerminationMethod='Truncated', ... NumFrames=numframes); errorrate = comm.ErrorRate(ComputationDelay=0,ReceiveDelay=0);
Due to the computational complexity of the Viterbi decoding algorithm, loading multiple frames of signal data on the GPU and processing them in one call can reduce overall simulation time. To enable this implementation, the GPU-based Viterbi decoder System object contains a NumFrames property. Instead of using an external for-loop to process individual frames of data, you use the NumFrames property to configure the GPU-based Viterbi decoder System object to process multiple data frames. Generate numframes of binary data frames. To efficiently manage the data frames for processing by the GPU-based System objects, represent the transmission data frames as a gpuArray object.
numsymbols = 50; rate = 1/2; dataA = gpuArray.randi([0 1],rate*numsymbols*log2(M),numframes);
The error rate object does not support gpuArray objects or multichannel data, so you must retrieve the array from the GPU by using the gather (Parallel Computing Toolbox) function to compute the error rate on each frame of data in a for-loop. Perform the GPU-based encoding, modulation, AWGN, and demodulation inside a for-loop.
for ii = 1:numframes encodedData = gpuconvenc(dataA(:,ii)); modsig = gpupskmod(encodedData); noisysig = awgn(modsig,30); % SNR = 30 dB. Signal power = 0 dBW demodsig(:,ii) = gpupskdemod(noisysig); end
The GPU-based Viterbi decoder performs multiframe processing without a for-loop.
rxbits = gpuvitdec(demodsig(:)); errorStats = errorrate(gather(dataA(:)),gather(rxbits)); fprintf('BER = %f\nNumber of errors = %d\nTotal bits = %d', ... errorStats(1), errorStats(2), errorStats(3))
BER = 0.009900 Number of errors = 99 Total bits = 10000
MATLAB System Block Support for GPU-Based System Objects
If you are using MATLAB System (Simulink) blocks in your implementation, you can include these GPU-based System objects in them:
comm.gpu.BlockDeinterleavercomm.gpu.BlockInterleavercomm.gpu.ConvolutionalDeinterleavercomm.gpu.ConvolutionalEncodercomm.gpu.ConvolutionalInterleavercomm.gpu.PSKDemodulatorcomm.gpu.PSKModulatorcomm.gpu.TurboDecodercomm.gpu.ViterbiDecoder
You must simulate these GPU System objects using the Interpreted
execution option. Select this option explicitly from the
Simulate using parameter on the block mask; the default
value is Code generation.

See Also
Topics
- Run MATLAB Functions on a GPU (Parallel Computing Toolbox)
- GPU Computing Requirements (Parallel Computing Toolbox)
- C/C++ Code Generation