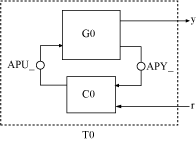
Set up the following control system for tuning with looptune. Then convert the setup to a systune problem and examine the results. These results reflect the structure of the control system model that looptune tunes. The results also reflect the tuning requirements implicitly enforced when tuning with looptune.
For this example, the 2-by-2 plant G is represented by:
The fixed-structure controller, C, includes three components: the 2-by-2 decoupling matrix D and two PI controllers PI_L and PI_V. The signals r, y, and e are vector-valued signals of dimension 2.
Build a numeric model that represents the plant and a tunable model that represents the controller. Name all inputs and outputs as in the diagram, so that looptune and looptuneSetup know how to interconnect the plant and controller via the control and measurement signals.
This system is now ready for tuning with looptune, using tuning goals that you specify. For example, specify a target bandwidth range. Create a tuning requirement that imposes reference tracking in both channels of the system with a response time of 15 s, and a disturbance rejection requirement.
Final: Peak gain = 1, Iterations = 42
Achieved target gain value TargetGain=1.
looptune successfully tunes the system to these requirements. However, you might want to switch to systune to take advantage of additional flexibility in configuring your problem. For example, instead of tuning both channels to a loop bandwidth inside wc, you might want to specify different crossover frequencies for each loop. Or, you might want to enforce the tuning requirements TR and DR as hard constraints, and add other requirements as soft requirements.
Convert the looptune input arguments to a set of input arguments for systune.
This command returns a set of arguments you can provide to systune for equivalent results to tuning with looptune. In other words, the following command is equivalent to the previous looptune command.
Final: Peak gain = 1, Iterations = 42
Achieved target gain value TargetGain=1.
Examine the arguments returned by looptuneSetup.
Generalized continuous-time state-space model with 0 outputs, 2 inputs, 4 states, and the following blocks:
APU_: Analysis point, 2 channels, 1 occurrences.
APY_: Analysis point, 2 channels, 1 occurrences.
Decoupler: Tunable 2x2 gain, 1 occurrences.
PI_L: Tunable PID controller, 1 occurrences.
PI_V: Tunable PID controller, 1 occurrences.
Type "ss(T0)" to see the current value and "T0.Blocks" to interact with the blocks.
The software constructs the closed-loop control system for systune by connecting the plant and controller at their control and measurement signals, and inserting a two-channel AnalysisPoint block at each of the connection locations, as illustrated in the following diagram.
When tuning the control system of this example with looptune, all requirements are treated as soft requirements. Therefore, HardReqs is empty. SoftReqs is an array of TuningGoal requirements. These requirements together enforce the bandwidth and margins of the looptune command, plus the additional requirements that you specified.
SoftReqs=5×1 heterogeneous SystemLevel (LoopShape, Tracking, Rejection, ...) array with properties:
Models
Openings
Name
Examine the first entry in SoftReqs.
ans =
LoopShape with properties:
LoopGain: [1x1 zpk]
CrossTol: 0.3495
Focus: [0 Inf]
Stabilize: 1
LoopScaling: 'on'
Location: {2x1 cell}
Models: NaN
Openings: {0x1 cell}
Name: 'Open loop CG'
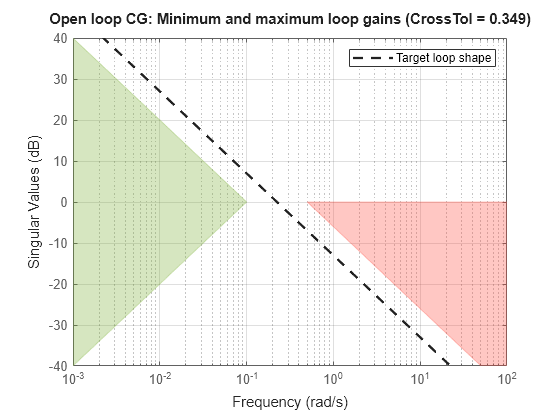
looptuneSetup expresses the target crossover frequency range wc as a TuningGoal.LoopShape requirement. This requirement constrains the open-loop gain profile to the loop shape stored in the LoopGain property, with a crossover frequency and crossover tolerance (CrossTol) determined by wc. Examine this loop shape.
The target crossover is expressed as an integrator gain profile with a crossover between 0.1 and 0.5 rad/s, as specified by wc. If you want to specify a different loop shape, you can alter this TuningGoal.LoopShape requirement before providing it to systune.
looptune also tunes to default stability margins that you can change using looptuneOptions. For systune, stability margins are specified using TuningGoal.Margins requirements. Here, looptuneSetup has expressed the default stability margins of looptune as soft TuningGoal.Margins requirements. For example, examine the fourth entry in SoftReqs.
ans =
Margins with properties:
GainMargin: 7.6000
PhaseMargin: 45
ScalingOrder: 0
Focus: [0 Inf]
Location: {2x1 cell}
Models: NaN
Openings: {0x1 cell}
Name: 'Margins at plant inputs'
The last entry in SoftReqs is a similar TuningGoal.Margins requirement constraining the margins at the plant outputs. looptune enforces these margins as soft requirements. If you want to convert them to hard constraints, pass them to systune in the input vector HardReqs instead of the input vector SoftReqs.