创建离散时间模型
此示例说明如何使用 tf、zpk、ss 和 frd 命令创建离散时间线性模型。
指定离散时间模型
Control System Toolbox™ 可用于创建连续时间模型和离散时间模型。创建离散时间模型的语法与创建连续时间模型的语法相似,不同之处在于您还必须提供采样时间(采样间隔以秒为单位)。
例如,要指定离散时间传递函数:
(采样周期 Ts = 0.1 s),请键入:
num = [ 1 -1 ]; den = [ 1 -1.85 0.9 ]; H = tf(num,den,0.1)
H =
z - 1
------------------
z^2 - 1.85 z + 0.9
Sample time: 0.1 seconds
Discrete-time transfer function.
Model Properties
或者,采用等效方式:
z = tf('z',0.1);
H = (z - 1) / (z^2 - 1.85*z + 0.9);同样,要指定离散时间状态空间模型:
(采样周期 Ts = 0.1 s),请键入:
sys = ss(.5,1,.2,0,0.1);
识别离散时间系统
有几种方法可以确定您的 LTI 模型是否为离散模型:
显示画面显示非零采样时间值
sys.Ts或get(sys,'Ts')返回非零采样时间值。isdt(sys)返回 true。
例如,对于上面指定的传递函数 H,
H.Ts
ans = 0.1000
isdt(H)
ans = logical
1
您还可以通过寻找以下特性来发现离散时间系统:
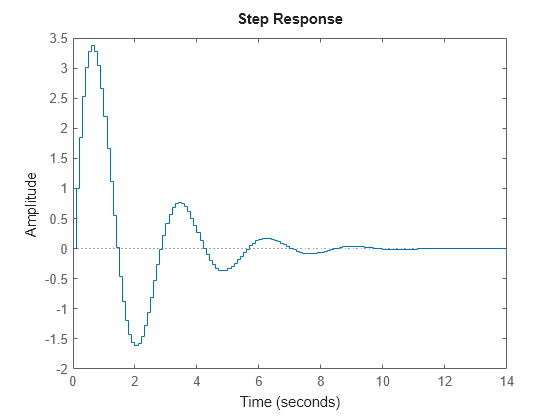
时间响应图 - 响应曲线因其采样数据的性质而呈阶梯状
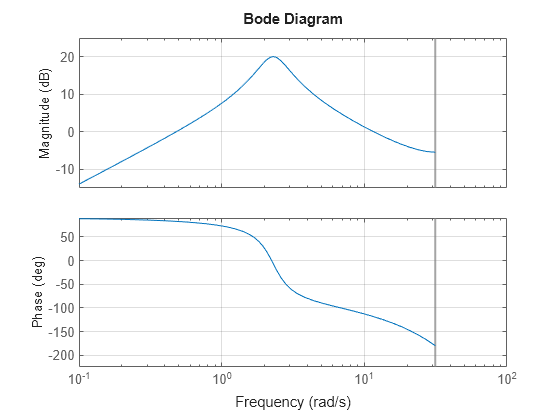
波特图 - 有一条垂直条标记奈奎斯特频率(pi 除以采样时间)。
以下各图显示这些特性:
step(H)
bode(H), grid