DC 电机控制
此示例比较用于跟踪设定点命令和降低对负载扰动的灵敏度的三种 DC 电机控制方法:
前馈命令
积分反馈控制
LQR 调节
请参阅“快速入门:构建模型”了解有关 DC 电机模型的更多详细信息。
问题陈述
在电枢控制的 DC 电机中,施加的电压 Va 控制轴的角速度 w。

此示例展示了两种 DC 电机控制方法,用于降低 w 对负载变化(电机负载所抵抗的转矩变化)的灵敏度。

上图显示的是 DC 电机的一个简化模型。转矩 Td 对负载扰动进行建模。您必须尽量减少这种扰动引起的转速变化。
对于此示例,物理常量为:
R = 2.0; % Ohms L = 0.5; % Henrys Km = 0.1; % torque constant Kb = 0.1; % back emf constant Kf = 0.2; % Nms J = 0.02; % kg.m^2/s^2
首先构造具有两个输入(Va、Td)和一个输出 (w) 的 DC 电机的状态空间模型:
h1 = tf(Km,[L R]); % armature h2 = tf(1,[J Kf]); % eqn of motion dcm = ss(h2) * [h1 , 1]; % w = h2 * (h1*Va + Td) dcm = feedback(dcm,Kb,1,1); % close back emf loop
注意:使用状态空间形式进行计算以最小化模型阶数。
现在绘制角速度对电压 Va 阶跃变化的响应:
figure stepplot(dcm(1));
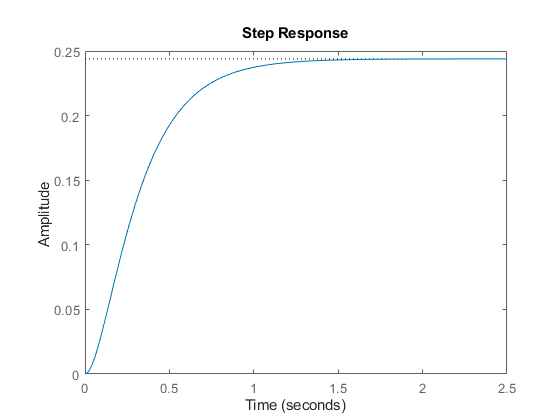
右键点击绘图并选择“特征: 稳定时间”以显示稳定时间。
前馈 DC 电机控制设计
您可以使用这一简单的前馈控制结构来命令角速度 w 达到给定值 w_ref。
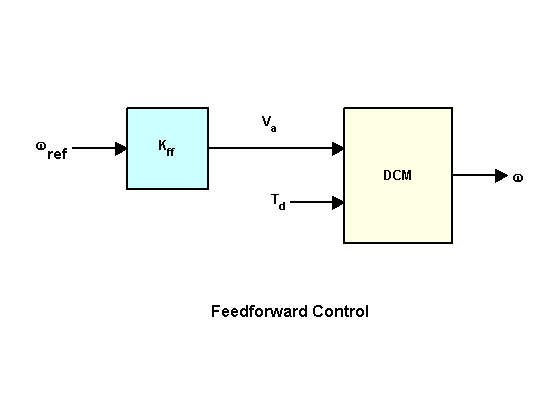
前馈增益 Kff 应设置为从 Va 到 w 的 DC 增益的倒数。
Kff = 1/dcgain(dcm(1))
Kff =
4.1000
为了评估在负载扰动情况下的前馈设计,仿真在 t=5 至 t=10 秒之间存在扰动 Td = -0.1Nm 时对阶跃命令 w_ref=1 的响应:
t = 0:0.1:15; Td = -0.1 * (t>5 & t<10); % load disturbance u = [ones(size(t)) ; Td]; % w_ref=1 and Td cl_ff = dcm * diag([Kff,1]); % add feedforward gain cl_ff.InputName = {'w_ref','Td'}; cl_ff.OutputName = 'w'; figure lp = lsimplot(cl_ff,u,t); title('Setpoint tracking and disturbance rejection') legend('cl\_ff'); % Annotate plot line([5,5],[.2,.3]); line([10,10],[.2,.3]); text(7.5,.25,{'disturbance','T_d = -0.1Nm'},... 'vertic','middle','horiz','center','color','r');

显然,前馈控制处理负载扰动效果不佳。
反馈 DC 电机控制设计
接下来尝试下面所示的反馈控制结构。

为了强制应用零稳态误差,使用以下形式的积分控制
C(s) = K/s
where K is to be determined.
要确定增益 K,可以使用根轨迹方法,将其应用于开环传递函数 1/s * transfer(Va->w):
figure
rp = rlocusplot(tf(1,[1 0]) * dcm(1));
rp.FrequencyUnit = "rad/s";
xlim([-15 5]);
ylim([-15 15]);

点击曲线以读取增益值和相关信息。此处合理的选择是 K = 5。控制系统设计器是用于执行此类设计的交互式 UI。
在相同测试用例的基础上,将此新设计与初始前馈设计进行比较:
K = 5; C = tf(K,[1 0]); % compensator K/s cl_rloc = feedback(dcm * append(C,1),1,1,1); figure lp2 = lsimplot(cl_ff,cl_rloc,u,t); cl_rloc.InputName = {'w_ref','Td'}; cl_rloc.OutputName = 'w'; title('Setpoint tracking and disturbance rejection') legend('feedforward','feedback w/ rlocus','Location','NorthWest');
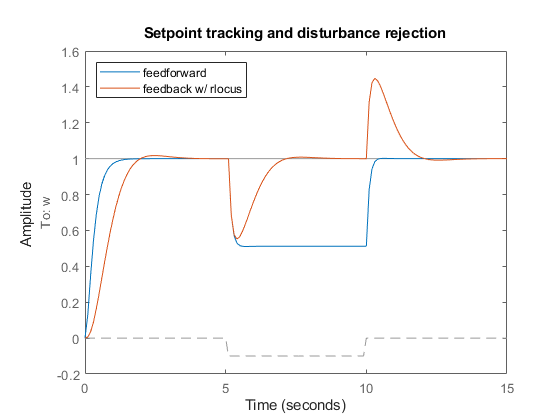
根轨迹设计能更好地抵抗负载扰动。
LQR DC 电机控制设计
为了进一步提高性能,尝试为下面所示的反馈结构设计线性二次调节器 (LQR)。

除了误差积分之外,LQR 方案还使用状态向量 x=(i,w) 来合成驱动电压 Va。产生的电压形式如下
Va = K1 * w + K2 * w/s + K3 * i
where i is the armature current.
为了更好地抗扰,使用对大积分误差进行罚分的代价函数,例如下面这个代价函数

其中
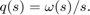
此代价函数的最佳 LQR 增益计算如下:
dc_aug = [1 ; tf(1,[1 0])] * dcm(1); % add output w/s to DC motor model
K_lqr = lqry(dc_aug,[1 0;0 20],0.01);
接下来,推导用于仿真目的的闭环模型:
P = augstate(dcm); % inputs:Va,Td outputs:w,x C = K_lqr * append(tf(1,[1 0]),1,1); % compensator including 1/s OL = P * append(C,1); % open loop CL = feedback(OL,eye(3),1:3,1:3); % close feedback loops cl_lqr = CL(1,[1 4]); % extract transfer (w_ref,Td)->w
下图比较了三种 DC 电机控制设计的闭环波特图。
figure bodeplot(cl_ff,cl_rloc,cl_lqr);

点击曲线以辨识系统或检查数据。
DC 电机控制设计的比较
最后,我们基于仿真测试用例比较这三种 DC 电机控制设计:
figure lp3 = lsimplot(cl_ff,cl_rloc,cl_lqr,u,t); title('Setpoint tracking and disturbance rejection') legend('feedforward','feedback (rlocus)','feedback (LQR)','Location','NorthWest');
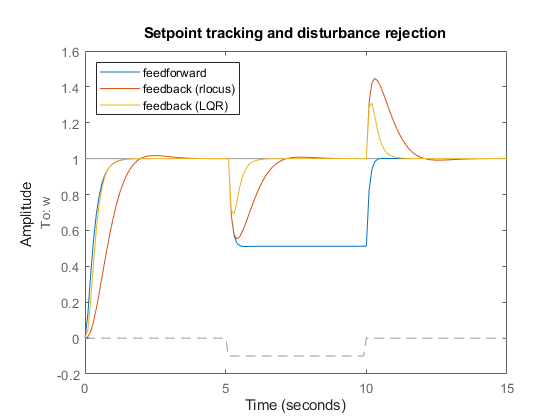
由于 LQR 补偿器具有额外的自由度,该补偿器在抵抗负载扰动方面表现最佳(仅限于此处讨论的三种 DC 电机控制设计)。