Reduce Model Order Using Model Reducer App
This example shows how to reduce model order while preserving important dynamics using the Model Reducer app. This example illustrates the Balanced Truncation method, which eliminates states based on their energy contributions to the system response.
Open Model Reducer with a Building Model
This example uses a model of the Los Angeles University Hospital building. The building has eight floors, each with three degrees of freedom: two displacements and one rotation. The input-output relationship for any one of these displacements is represented as a 48-state model, where each state represents a displacement or its rate of change (velocity). Load the building model and open Model Reducer with that model.
load building.mat
modelReducer(G)

Open the Balanced Truncation Tab
Model Reducer has three model reduction methods: Balanced Truncation, Modal Truncation, and Pole/Zero Simplification. For this example, click Balanced Truncation.

Model Reducer opens the Balanced Truncation tab and automatically generates a reduced-order model. The top plot compares the original and reduced model in the frequency domain. The bottom plot shows the energy contribution of each state, where the states are sorted from high energy to low energy. The order of the reduced model, 14, is highlighted in the bar chart. In the reduced model, all states with lower energy contribution than this one are discarded.
Compute Multiple Approximations
Suppose that you want to preserve the first, second, and third peaks of the model response, around 5.2 rad/s, 13 rad/s, and 25 rad/s. Try other model orders to see whether you can achieve this goal with a lower model order. Compute a 5th-order and a 10th-order approximation in one of the following ways:
In the Reduced model orders text box, enter
[5 10].In the state-contribution plot, ctrl-click the bars for state 5 and state 10.
Model Reducer computes two new reduced-order models and displays them on the response plot with the original model G. To examine the three peaks more closely, Zoom in on the relevant frequency range. The 10th-order model captures the three peaks successfully, while the 5th-order model only approximates the first two peaks. (For information about zooming and other interactions with the analysis plots, see Visualize Reduced-Order Models in Model Reducer App.)

Compare Reduced Models with Different Visualizations
In addition to the frequency response plot of all three models, Model Reducer lets you examine the absolute and relative error between the original and reduced models. To see the error difference between the building and reduced models, select Absolute error from the Comparison plot list.
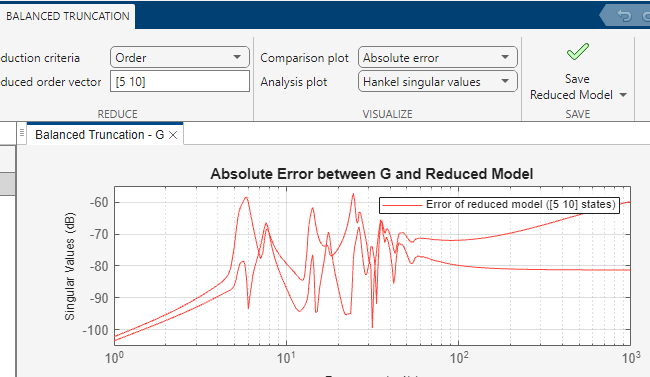
The 5th-order reduced model has at most -60dB error in the frequency region of the first two peaks, below about 30 rad/s. The error increases at higher frequencies. The 10th-order reduced model has smaller error over all frequencies.
Create Reduced Models in Data Browser
Store the reduced models in the data browser by clicking Save Reduced Model. The 5th-order and 10th-order reduced models appear in the data browser with names GReduced5 and Greduced10.
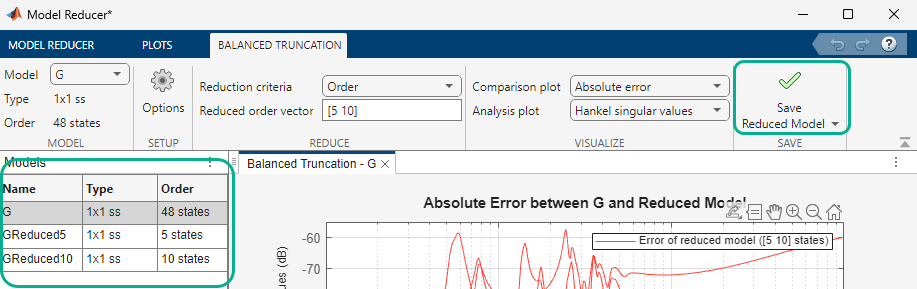
You can continue to change the model-reduction parameters and generate additional reduced models. As you do so, GReduced5 and Greduced10 remain unchanged in the data browser.
Focus on Dynamics at Particular Frequencies
By default, balanced truncation in Model Reducer preserves DC gain, matching the steady-state response of the original and reduced models. To change this setting, click Options.

Clear the Preserve DC Gain checkbox on the dialog to better approximate high-frequency dynamics.

Click OK to apply the setting.
Model Reducer computes new reduced models. The error in the high-frequency region is decreased at the cost of a slight increase in error at low frequencies.

You can also focus the balanced truncation on the model dynamics in a particular frequency interval. For example, approximate only the second peak of the building model around 13 rad/s. Select the Model response plot to see the Bode plots of models and click Options.
In the Focus section, click ![]() to add a frequency interval. For this model, specify
to add a frequency interval. For this model, specify 10 as Lower cutoff and 22 as Upper cutoff.
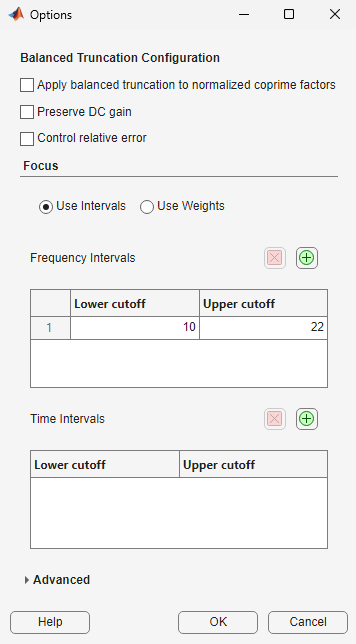
Click OK. Model Reducer analyzes state contributions in the highlighted frequency interval only.

The 5th-order reduced model captures the essential dynamics. The 10th-order model has almost the same dynamics as the original building model within this frequency range.
You can drag the boundaries to change the frequency range interactively. As you change the frequency interval, the Hankel Singular Value plot reflects the changes in the energy contributions of the states.
Optionally, store these additional models in the data browser by clicking Save Reduced Model.
Compare Models in Time Domain
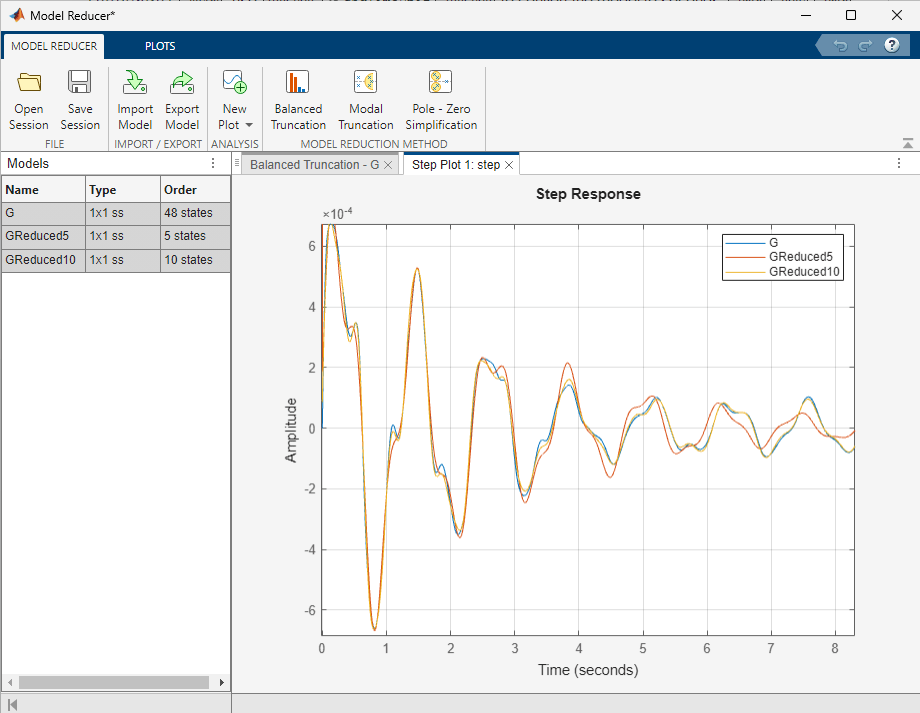
You can compare time-domain responses of the stored reduced models and the original in the Plots tab. In the data browser, control-click to select the models you want to compare, G, GReduced5, and GReduced10. Then, click Step. Model Reducer creates a step plot with all three models.
Zooming on the transient behavior of this plot shows that GReduced10 captures the time domain behavior of the original model well. However, the response of GReduced5 deviates from the original model after about 3 seconds.
Export Model for Further Analysis
Comparison of the reduced and original models in the time and frequency domains shows that GReduced10 adequately captures the dynamics of interest. Export that model to the MATLAB® workspace for further analysis and design. In the Model Reducer tab, click Export Model. Clear the check boxes for G and Greduced5, and click Export to export Greduced10.

Greduced10 appears in the MATLAB workspace as a state-space (ss) model.