Measure Angular Position with an Incremental Rotary Encoder

Create a Data Acquisition Object

Create a data acquisition object and add an input channel with Position measurement type.

s = daq('ni');
ch1 = addinput(s, 'Dev1', 'ctr0', 'Position');

Configure Hardware

A rotary quadrature encoder outputs two quadrature signals, A and B, which provide information on the relative change in position and the direction of rotation. Optionally, some models also output an index or reference signal, Z, which is active once per revolution. You can use the Z signal to reset the counter position to a known reference value.

Connect A, B, and Z signal outputs from the encoder device to the proper DAQ input terminals specified by the DAQ device datasheet (PFI8, PFI10, and PFI9 for NI USB-6255). The correct terminals depend on the device model and the counter channel used, and can be listed by reading the following properties:

ch1.TerminalA

ans =

    'PFI8'

ch1.TerminalB

ans =

    'PFI10'

ch1.TerminalZ

ans =

    'PFI9'

Configure quadrature cycle encoding type (X1, X2, or X4). This corresponds to the number of counts (counter value increments or decrements) output by the encoder for each quadrature cycle (1, 2, or 4.), as specified in the encoder datasheet.

ch1.EncoderType = 'X1';

Read Encoder Position on Demand

The DAQ device counter hardware keeps track of the relative position changes signaled by the encoder. Use read to read an updated position from the counter input channel.

encoderPosition = read(s, 1, 'OutputFormat', 'Matrix')

encoderPosition =

     0

This example uses an optical encoder model with a resolution of 2500 quadrature cycles per shaft revolution, as specified in the encoder datasheet.

Convert counter values to angular position (in degrees) using the encoder resolution and the encoding type ('X1' in this case).

encoderCPR = 2500;
encoderPositionDeg = encoderPosition * 360/encoderCPR

encoderPositionDeg =

     0

Acquire Hardware-Timed Encoder Position Data

For applications where high time-resolution is required the data acquisition must be hardware-timed (clocked). As proof of concept, this example characterizes the motion of a swinging pendulum by measuring its angular position vs. time.

To acquire hardware-timed data from a counter input channel, NI DAQ devices require the use of an external clock or the use of a clock from another subsystem.

Add an analog input channel to the data acquisition object to automatically share this system's scan clock.

addinput(s, 'Dev1', 'ai0', 'Voltage');

Configure acquisition rate (samples/s) and acquisition duration in seconds.

s.Rate = 10000;
daqDuration = seconds(35);

Acquire data in the foreground.

[positionData, timestamps] = read(s, daqDuration, 'OutputFormat', 'Matrix');

By default, counter position readings are unsigned integer values. The counter channels of the DAQ device used in this example are 32-bit, so any counter value read will be in the range 0 to 2^32-1. Depending on the application, you may want to obtain signed position values (positive or negative) as decrementing the counter value past zero is a discontinuous wraparound to 2^32-1.

For 32-bit counter channels, use 2^31 as the threshold counter value for conversion to signed position values. The result is valid if the actual position value is in the range -2^31+1 to 2^31.

counterNBits = 32;
signedThreshold = 2^(counterNBits-1);
signedData = positionData(:,1);
signedData(signedData > signedThreshold) = signedData(signedData > signedThreshold) - 2^counterNBits;

Calculate encoder position data in degrees.

positionDataDeg = signedData * 360/encoderCPR;

Plot the signed angular position data acquired for the oscillatory motion of a pendulum.

figure
plot(timestamps, positionDataDeg);
xlabel('Time (s)');
ylabel('Angular position (deg.)');

Use the Z Signal to Reference the Relative Position to a Known Absolute Position

The A and B quadrature signals output by incremental rotary encoders provide only relative position information (direction of motion and changes in position). The optional reference signal Z is a single pulse output once per encoder shaft revolution at a predefined absolute location. Referencing the relative position value to the known absolute position reference allows an incremental rotary encoder to function as a pseudo-absolute position encoder. This is useful in accurate positioning applications (such as industrial automation, robotics, solar tracking, radar antenna or telescope positioning).

For incremental rotary encoders that provide a Z index signal output, the counter position value can be configured to be reset automatically to the known reference value.

Set the ZResetEnable and ZResetCondition properties.

ch1.ZResetEnable = true;

Configure the ZResetCondition, which is based on the A and B phase signals.

ch1.ZResetCondition = 'BothLow';

Specify the absolute reference position value ZResetValue to which the counter value will be reset.

ch1.ZResetValue = 0;

Acquire and plot a set of hardware-timed counter position data to show how you can use the encoder Z index signal to automatically reset the counter value to a known reference value.

[positionData2, timestamps2] = read(s, daqDuration, 'OutputFormat', 'matrix');

figure
plot(timestamps2, positionData2(:,1));
xlabel('Time (s)');
ylabel('Counter value for quadrature encoder (counts)');

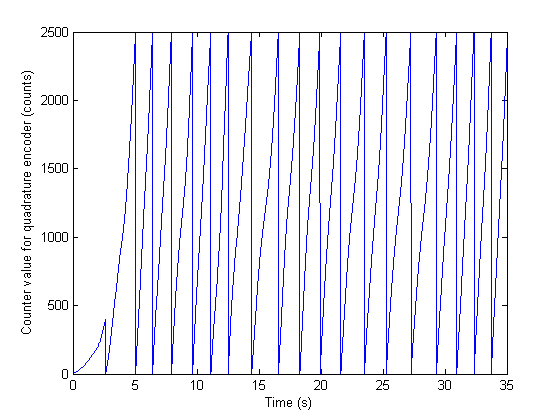
The acquired position data corresponds to a rotary encoder shaft that is rotating continuously. Notice that before the first time the counter value is reset the position value is not referenced to an absolute position, whereas the other counter reset events occur when the counter value is 2500 (the encoder CPR value).