lstmLayer
Long short-term memory (LSTM) layer for recurrent neural network (RNN)
Description
An LSTM layer is an RNN layer that learns long-term dependencies between time steps in time-series and sequence data.
The layer performs additive interactions, which can help improve gradient flow over long sequences during training.
Creation
Description
layer = lstmLayer(numHiddenUnits)NumHiddenUnits property.
layer = lstmLayer(numHiddenUnits,Name=Value)OutputMode, Activations, State, Parameters and Initialization, Learning Rate and Regularization, and
Name
properties using one or more name-value arguments.
Properties
LSTM
NumHiddenUnits — Number of hidden units
positive integer
Number of hidden units (also known as the hidden size), specified as a positive integer.
The number of hidden units corresponds to the amount of information that the layer remembers between time steps (the hidden state). The hidden state can contain information from all the previous time steps, regardless of the sequence length. If the number of hidden units is too large, then the layer can overfit to the training data. The hidden state does not limit the number of time steps that the layer processes in an iteration.
The layer outputs data with NumHiddenUnits channels.
To set this property, use the numHiddenUnits argument when you
create the LSTMLayer object. After you create a
LSTMLayer object, this property is read-only.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
OutputMode — Output mode
"sequence" (default) | "last"
Output mode, specified as one of these values:
"sequence"— Output the complete sequence."last"— Output the last time step of the sequence.
The LSTMLayer object stores this property as a character vector.
To set this property, use the corresponding name-value argument when you create the LSTMLayer object. After you create a LSTMLayer object, this property is read-only.
HasStateInputs — Flag for state inputs to layer
0 (false) (default) | 1 (true)
This property is read-only.
Flag for state inputs to the layer, specified as 0
(false) or 1 (true).
If the HasStateInputs property is 0
(false), then the layer has one input with the name
"in", which corresponds to the input data. In this case, the layer
uses the HiddenState and CellState properties for the layer operation.
If the HasStateInputs property is 1
(true), then the layer has three inputs with the names
"in", "hidden", and "cell",
which correspond to the input data, hidden state, and cell state, respectively. In this
case, the layer uses the values passed to these inputs for the layer operation. If HasStateInputs is 1
(true), then the HiddenState and
CellState properties must be empty.
HasStateOutputs — Flag for state outputs from layer
0 (false) (default) | 1 (true)
This property is read-only.
Flag for state outputs from the layer, specified as
0 (false) or
1
(true).
If the HasStateOutputs property is 0
(false), then the layer has one output with the name
"out", which corresponds to the output data.
If the HasStateOutputs property is 1
(true), then the layer has three outputs with the names
"out", "hidden", and
"cell", which correspond to the output data, hidden
state, and cell state, respectively. In this case, the layer also outputs the state
values that it computes.
InputSize — Input size
"auto" (default) | positive integer
This property is read-only.
Input size, specified as a positive integer or "auto". If
InputSize is "auto", then the software
automatically assigns the input size at training time.
If InputSize is "auto", then the
LSTMLayer object stores this property as a character
vector.
Data Types: double | char | string
Activations
StateActivationFunction — Activation function to update cell and hidden state
"tanh" (default) | "softsign" | "relu" (since R2024a)
This property is read-only.
Activation function to update the cell and hidden state, specified as one of these values:
"tanh"— Use the hyperbolic tangent function (tanh)."softsign"— Use the softsign function ."relu"(since R2024a) — Use the rectified linear unit (ReLU) function .
The software uses this option as the function in the calculations to update the cell and hidden state.
For more information on how an LSTM layer uses activation functions, see Long Short-Term Memory Layer.
The LSTMLayer object stores this property as a character vector.
GateActivationFunction — Activation function to apply to gates
"sigmoid" (default) | "hard-sigmoid"
Activation function to apply to the gates, specified as one of these values:
"sigmoid"— Use the sigmoid function, ."hard-sigmoid"— Use the hard sigmoid function,
The software uses this option as the function in the calculations for the layer gates.
The LSTMLayer object stores this property as a character vector.
To set this property, use the corresponding name-value argument when you create the LSTMLayer object. After you create a LSTMLayer object, this property is read-only.
State
CellState — Cell state
[] (default) | numeric vector
Cell state to use in the layer operation, specified as a NumHiddenUnits-by-1 numeric vector. This value corresponds to the initial cell state when data is passed to the layer.
After you set this property manually, calls to the resetState
function set the cell state to this value.
If HasStateInputs is 1
(true), then the CellState
property must be empty.
Data Types: single | double
HiddenState — Hidden state
[] (default) | numeric vector
Hidden state to use in the layer operation, specified as a
NumHiddenUnits-by-1 numeric vector. This value corresponds to the
initial hidden state when data is passed to the layer.
After you set this property manually, calls to the resetState
function set the hidden state to this value.
If HasStateInputs is 1
(true), then the HiddenState
property must be empty.
Data Types: single | double
Parameters and Initialization
InputWeightsInitializer — Function to initialize input weights
"glorot" (default) | "he" | "orthogonal" | "narrow-normal" | "zeros" | "ones" | function handle
Function to initialize the input weights, specified as one of the following:
"glorot"– Initialize the input weights with the Glorot initializer [2] (also known as Xavier initializer). The Glorot initializer independently samples from a uniform distribution with zero mean and variance2/(InputSize + numOut), wherenumOut = 4*NumHiddenUnits."he"– Initialize the input weights with the He initializer [3]. The He initializer samples from a normal distribution with zero mean and variance2/InputSize."orthogonal"– Initialize the input weights with Q, the orthogonal matrix given by the QR decomposition of Z = QR for a random matrix Z sampled from a unit normal distribution. [4]"narrow-normal"– Initialize the input weights by independently sampling from a normal distribution with zero mean and standard deviation 0.01."zeros"– Initialize the input weights with zeros."ones"– Initialize the input weights with ones.Function handle – Initialize the input weights with a custom function. If you specify a function handle, then the function must be of the form
weights = func(sz), whereszis the size of the input weights.
The layer only initializes the input weights when the
InputWeights property is empty.
The LSTMLayer object stores this property as a character vector or a
function handle.
Data Types: char | string | function_handle
RecurrentWeightsInitializer — Function to initialize recurrent weights
"orthogonal" (default) | "glorot" | "he" | "narrow-normal" | "zeros" | "ones" | function handle
Function to initialize the recurrent weights, specified as one of the following:
"orthogonal"– Initialize the recurrent weights with Q, the orthogonal matrix given by the QR decomposition of Z = QR for a random matrix Z sampled from a unit normal distribution. [4]"glorot"– Initialize the recurrent weights with the Glorot initializer [2] (also known as Xavier initializer). The Glorot initializer independently samples from a uniform distribution with zero mean and variance2/(numIn + numOut), wherenumIn = NumHiddenUnitsandnumOut = 4*NumHiddenUnits."he"– Initialize the recurrent weights with the He initializer [3]. The He initializer samples from a normal distribution with zero mean and variance2/NumHiddenUnits."narrow-normal"– Initialize the recurrent weights by independently sampling from a normal distribution with zero mean and standard deviation 0.01."zeros"– Initialize the recurrent weights with zeros."ones"– Initialize the recurrent weights with ones.Function handle – Initialize the recurrent weights with a custom function. If you specify a function handle, then the function must be of the form
weights = func(sz), whereszis the size of the recurrent weights.
The layer only initializes the recurrent weights when the
RecurrentWeights property is empty.
The LSTMLayer object stores this property as a character vector or a
function handle.
Data Types: char | string | function_handle
BiasInitializer — Function to initialize bias
"unit-forget-gate" (default) | "narrow-normal" | "ones" | function handle
Function to initialize the bias, specified as one of these values:
"unit-forget-gate"— Initialize the forget gate bias with ones and the remaining biases with zeros."narrow-normal"— Initialize the bias by independently sampling from a normal distribution with zero mean and a standard deviation of 0.01."ones"— Initialize the bias with ones.Function handle — Initialize the bias with a custom function. If you specify a function handle, then the function must be of the form
bias = func(sz), whereszis the size of the bias.
The layer only initializes the bias when the Bias property is
empty.
The LSTMLayer object stores this property as a character vector or a
function handle.
Data Types: char | string | function_handle
InputWeights — Input weights
[] (default) | matrix
Input weights, specified as a matrix.
The input weight matrix is a concatenation of the four input weight matrices for the components (gates) in the LSTM layer. The four matrices are concatenated vertically in the following order:
Input gate
Forget gate
Cell candidate
Output gate
The input weights are learnable parameters. When you train a
neural network using the trainnet function,
if InputWeights is nonempty, then the software uses the
InputWeights property as the initial value. If InputWeights is empty, then the software uses the initializer
specified by InputWeightsInitializer.
At training time, InputWeights is a
4*NumHiddenUnits-by-InputSize
matrix.
RecurrentWeights — Recurrent weights
[] (default) | matrix
Recurrent weights, specified as a matrix.
The recurrent weight matrix is a concatenation of the four recurrent weight matrices for the components (gates) in the LSTM layer. The four matrices are vertically concatenated in the following order:
Input gate
Forget gate
Cell candidate
Output gate
The recurrent weights are learnable parameters. When you train
an RNN using the trainnet function,
if RecurrentWeights is nonempty, then the software uses the
RecurrentWeights property as the initial value. If
RecurrentWeights is empty, then the software uses the
initializer specified by RecurrentWeightsInitializer.
At training time RecurrentWeights
is a
4*NumHiddenUnits-by-NumHiddenUnits
matrix.
Bias — Layer biases
[]
(default) | numeric vector
Layer biases, specified as a numeric vector.
The bias vector is a concatenation of the four bias vectors for the components (gates) in the layer. The layer vertically concatenates the four vectors in this order:
Input gate
Forget gate
Cell candidate
Output gate
The layer biases are learnable parameters. When you train a neural network, if Bias is nonempty, then the trainnet and trainNetwork functions use the Bias property as the initial value. If Bias is empty, then software uses the initializer specified by BiasInitializer.
At training time, Bias is a
4*NumHiddenUnits-by-1 numeric vector.
Learning Rate and Regularization
InputWeightsLearnRateFactor — Learning rate factor for input weights
1 (default) | nonnegative scalar | 1-by-4 numeric vector
Learning rate factor for the input weights, specified as a nonnegative scalar or a 1-by-4 numeric vector.
The software multiplies this factor by the global learning rate
to determine the learning rate factor for the input weights of the layer. For example, if
InputWeightsLearnRateFactor is 2, then the learning
rate factor for the input weights of the layer is twice the current global learning rate. The
software determines the global learning rate based on the settings you specify with the
trainingOptions function.
To control the value of the learning rate factor for the four individual matrices in
InputWeights, specify a 1-by-4 vector. The
entries of InputWeightsLearnRateFactor correspond to
the learning rate factor of these components:
Input gate
Forget gate
Cell candidate
Output gate
To specify the same value for all the matrices, specify a nonnegative scalar.
Example: 2
Example: [1 2 1 1]
RecurrentWeightsLearnRateFactor — Learning rate factor for recurrent weights
1 (default) | nonnegative scalar | 1-by-4 numeric vector
Learning rate factor for the recurrent weights, specified as a nonnegative scalar or a 1-by-4 numeric vector.
The software multiplies this factor by the global learning rate
to determine the learning rate for the recurrent weights of the layer. For example, if
RecurrentWeightsLearnRateFactor is 2, then the
learning rate for the recurrent weights of the layer is twice the current global learning rate.
The software determines the global learning rate based on the settings you specify using the
trainingOptions function.
To control the value of the learning rate factor for the four individual matrices in
RecurrentWeights, specify a 1-by-4 vector. The
entries of RecurrentWeightsLearnRateFactor correspond
to the learning rate factor of these components:
Input gate
Forget gate
Cell candidate
Output gate
To specify the same value for all the matrices, specify a nonnegative scalar.
Example: 2
Example: [1 2 1 1]
BiasLearnRateFactor — Learning rate factor for biases
1 (default) | nonnegative scalar | 1-by-4 numeric vector
Learning rate factor for the biases, specified as a nonnegative scalar or a 1-by-4 numeric vector.
The software multiplies this factor by the global learning rate to determine the learning rate for the biases in this layer. For example, if BiasLearnRateFactor is 2, then the learning rate for the biases in the layer is twice the current global learning rate. The software determines the global learning rate based on the settings you specify using the trainingOptions function.
To control the value of the learning rate factor for the four individual vectors in
Bias, specify a 1-by-4 vector. The entries of
BiasLearnRateFactor correspond to the learning rate factor of
these components:
Input gate
Forget gate
Cell candidate
Output gate
To specify the same value for all the vectors, specify a nonnegative scalar.
Example:
2
Example:
[1 2 1 1]
InputWeightsL2Factor — L2 regularization factor for input weights
1 (default) | nonnegative scalar | 1-by-4 numeric vector
L2 regularization factor for the input weights, specified as a nonnegative scalar or a 1-by-4 numeric vector.
The software multiplies this factor by the global
L2 regularization factor to determine the
L2 regularization factor for the input weights
of the layer. For example, if InputWeightsL2Factor is 2,
then the L2 regularization factor for the input
weights of the layer is twice the current global L2
regularization factor. The software determines the L2
regularization factor based on the settings you specify using the trainingOptions function.
To control the value of the L2
regularization factor for the four individual matrices in
InputWeights, specify a 1-by-4 vector. The
entries of InputWeightsL2Factor correspond to the
L2 regularization
factor of these components:
Input gate
Forget gate
Cell candidate
Output gate
To specify the same value for all the matrices, specify a nonnegative scalar.
Example: 2
Example:
[1 2 1 1]
RecurrentWeightsL2Factor — L2 regularization factor for recurrent weights
1 (default) | nonnegative scalar | 1-by-4 numeric vector
L2 regularization factor for the recurrent weights, specified as a nonnegative scalar or a 1-by-4 numeric vector.
The software multiplies this factor by the global
L2 regularization factor to determine the
L2 regularization factor for the recurrent
weights of the layer. For example, if RecurrentWeightsL2Factor is
2, then the L2 regularization
factor for the recurrent weights of the layer is twice the current global
L2 regularization factor. The software
determines the L2 regularization factor based on the
settings you specify using the trainingOptions function.
To control the value of the L2
regularization factor for the four individual matrices in
RecurrentWeights, specify a 1-by-4 vector. The
entries of RecurrentWeightsL2Factor correspond to the
L2 regularization
factor of these components:
Input gate
Forget gate
Cell candidate
Output gate
To specify the same value for all the matrices, specify a nonnegative scalar.
Example: 2
Example:
[1 2 1 1]
BiasL2Factor — L2 regularization factor for biases
0 (default) | nonnegative scalar | 1-by-4 numeric vector
L2 regularization factor for the biases, specified as a nonnegative scalar or a 1-by-4 numeric vector.
The software multiplies this factor by the global L2 regularization factor to determine the L2 regularization for the biases in this layer. For example, if BiasL2Factor is 2, then the L2 regularization for the biases in this layer is twice the global L2 regularization factor. The software determines the global L2 regularization factor based on the settings you specify using the trainingOptions function.
To control the value of the L2
regularization factor for the four individual vectors in Bias,
specify a 1-by-4 vector. The entries of BiasL2Factor correspond to
the L2 regularization factor of these
components:
Input gate
Forget gate
Cell candidate
Output gate
To specify the same value for all the vectors, specify a nonnegative scalar.
Example:
2
Example:
[1 2 1 1]
Layer
Name — Layer name
"" (default) | character vector | string scalar
NumInputs — Number of inputs
1 | 3
This property is read-only.
Number of inputs to the layer.
If the HasStateInputs property is 0
(false), then the layer has one input with the name
"in", which corresponds to the input data. In this case, the layer
uses the HiddenState and CellState properties for the layer operation.
If the HasStateInputs property is 1
(true), then the layer has three inputs with the names
"in", "hidden", and "cell",
which correspond to the input data, hidden state, and cell state, respectively. In this
case, the layer uses the values passed to these inputs for the layer operation. If HasStateInputs is 1
(true), then the HiddenState and
CellState properties must be empty.
Data Types: double
InputNames — Input names
"in" | ["in" "hidden" "cell"]
This property is read-only.
Input names of the layer.
If the HasStateInputs property is 0
(false), then the layer has one input with the name
"in", which corresponds to the input data. In this case, the layer
uses the HiddenState and CellState properties for the layer operation.
If the HasStateInputs property is 1
(true), then the layer has three inputs with the names
"in", "hidden", and "cell",
which correspond to the input data, hidden state, and cell state, respectively. In this
case, the layer uses the values passed to these inputs for the layer operation. If HasStateInputs is 1
(true), then the HiddenState and
CellState properties must be empty.
The LSTMLayer object stores this property as a cell array of character
vectors.
NumOutputs — Number of outputs
1 | 3
This property is read-only.
Number of outputs to the layer.
If the HasStateOutputs property is 0
(false), then the layer has one output with the name
"out", which corresponds to the output data.
If the HasStateOutputs property is 1
(true), then the layer has three outputs with the names
"out", "hidden", and
"cell", which correspond to the output data, hidden
state, and cell state, respectively. In this case, the layer also outputs the state
values that it computes.
Data Types: double
OutputNames — Output names
"out" | ["out" "hidden" "cell"]
This property is read-only.
Output names of the layer.
If the HasStateOutputs property is 0
(false), then the layer has one output with the name
"out", which corresponds to the output data.
If the HasStateOutputs property is 1
(true), then the layer has three outputs with the names
"out", "hidden", and
"cell", which correspond to the output data, hidden
state, and cell state, respectively. In this case, the layer also outputs the state
values that it computes.
The LSTMLayer object stores this property as a cell array of character
vectors.
Examples
Create LSTM Layer
Create an LSTM layer with the name "lstm1" and 100 hidden units.
layer = lstmLayer(100,Name="lstm1")layer =
LSTMLayer with properties:
Name: 'lstm1'
InputNames: {'in'}
OutputNames: {'out'}
NumInputs: 1
NumOutputs: 1
HasStateInputs: 0
HasStateOutputs: 0
Hyperparameters
InputSize: 'auto'
NumHiddenUnits: 100
OutputMode: 'sequence'
StateActivationFunction: 'tanh'
GateActivationFunction: 'sigmoid'
Learnable Parameters
InputWeights: []
RecurrentWeights: []
Bias: []
State Parameters
HiddenState: []
CellState: []
Use properties method to see a list of all properties.
Include an LSTM layer in a Layer array.
inputSize = 12;
numHiddenUnits = 100;
numClasses = 9;
layers = [ ...
sequenceInputLayer(inputSize)
lstmLayer(numHiddenUnits)
fullyConnectedLayer(numClasses)
softmaxLayer]layers =
4x1 Layer array with layers:
1 '' Sequence Input Sequence input with 12 dimensions
2 '' LSTM LSTM with 100 hidden units
3 '' Fully Connected 9 fully connected layer
4 '' Softmax softmax
Train Network for Sequence Classification
Train a deep learning LSTM network for sequence-to-label classification.
Load the example data from WaveformData.mat. The data is a numObservations-by-1 cell array of sequences, where numObservations is the number of sequences. Each sequence is a numTimeSteps-by-numChannels numeric array, where numTimeSteps is the number of time steps of the sequence and numChannels is the number of channels of the sequence.
load WaveformDataVisualize some of the sequences in a plot.
numChannels = size(data{1},2);
idx = [3 4 5 12];
figure
tiledlayout(2,2)
for i = 1:4
nexttile
stackedplot(data{idx(i)},DisplayLabels="Channel "+string(1:numChannels))
xlabel("Time Step")
title("Class: " + string(labels(idx(i))))
end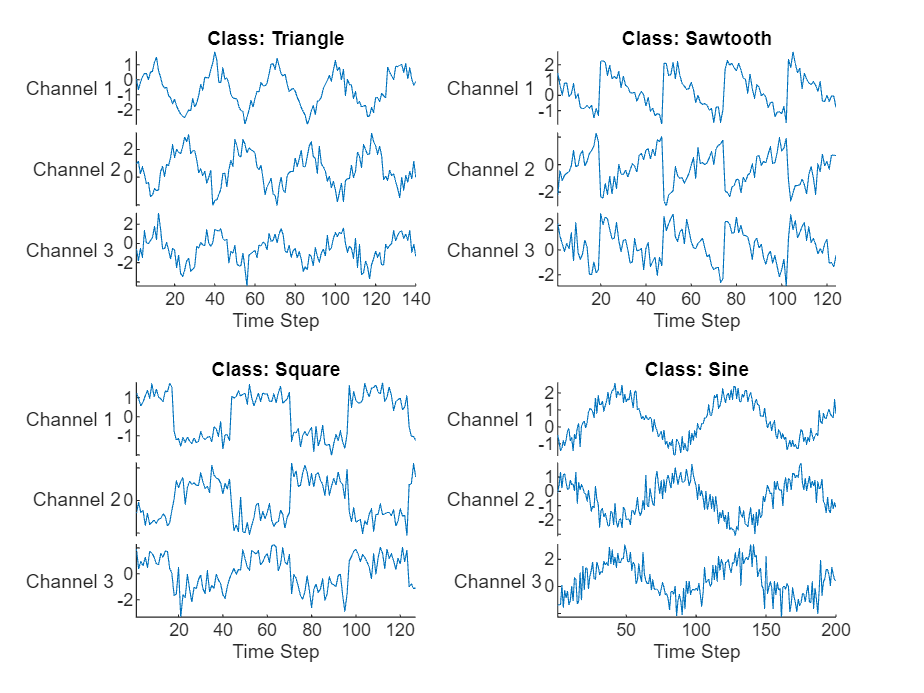
View the class names.
classNames = categories(labels)
classNames = 4×1 cell
{'Sawtooth'}
{'Sine' }
{'Square' }
{'Triangle'}
Set aside data for testing. Partition the data into a training set containing 90% of the data and a test set containing the remaining 10% of the data. To partition the data, use the trainingPartitions function, attached to this example as a supporting file. To access this file, open the example as a live script.
numObservations = numel(data); [idxTrain,idxTest] = trainingPartitions(numObservations, [0.9 0.1]); XTrain = data(idxTrain); TTrain = labels(idxTrain); XTest = data(idxTest); TTest = labels(idxTest);
Define the LSTM network architecture. Specify the input size as the number of channels of the input data. Specify an LSTM layer to have 120 hidden units and to output the last element of the sequence. Finally, include a fully connected with an output size that matches the number of classes, followed by a softmax layer.
numHiddenUnits = 120; numClasses = numel(categories(TTrain)); layers = [ ... sequenceInputLayer(numChannels) lstmLayer(numHiddenUnits,OutputMode="last") fullyConnectedLayer(numClasses) softmaxLayer]
layers =
4×1 Layer array with layers:
1 '' Sequence Input Sequence input with 3 dimensions
2 '' LSTM LSTM with 120 hidden units
3 '' Fully Connected 4 fully connected layer
4 '' Softmax softmax
Specify the training options. Train using the Adam solver with a learn rate of 0.01 and a gradient threshold of 1. Set the maximum number of epochs to 200 and shuffle every epoch. The software, by default, trains on a GPU if one is available. Using a GPU requires Parallel Computing Toolbox and a supported GPU device. For information on supported devices, see GPU Computing Requirements (Parallel Computing Toolbox).
options = trainingOptions("adam", ... MaxEpochs=200, ... InitialLearnRate=0.01,... Shuffle="every-epoch", ... GradientThreshold=1, ... Verbose=false, ... Metrics="accuracy", ... Plots="training-progress");
Train the LSTM network using the trainnet function. For classification, use cross-entropy loss.
net = trainnet(XTrain,TTrain,layers,"crossentropy",options);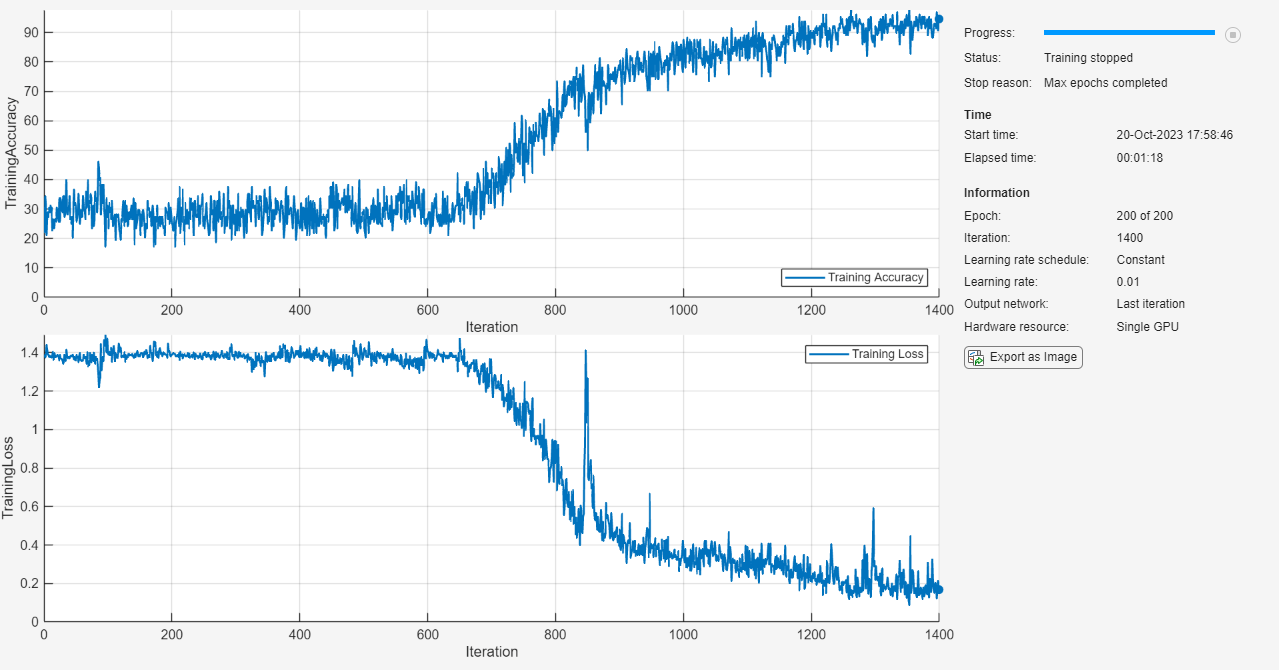
Classify the test data. Specify the same mini-batch size used for training.
scores = minibatchpredict(net,XTest); YTest = scores2label(scores,classNames);
Calculate the classification accuracy of the predictions.
acc = mean(YTest == TTest)
acc = 0.8700
Display the classification results in a confusion chart.
figure confusionchart(TTest,YTest)
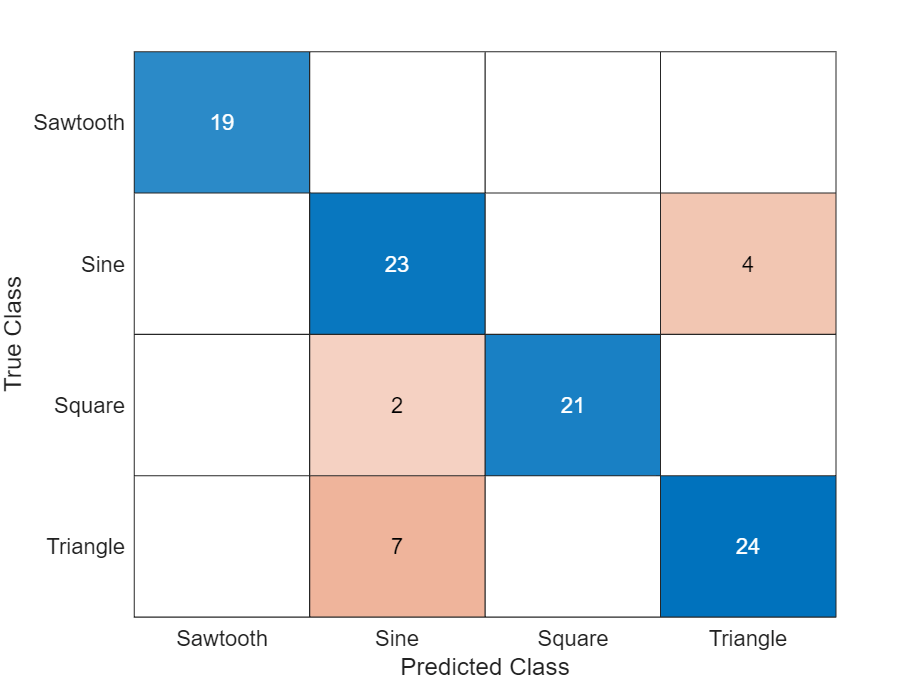
Classification LSTM Networks
To create an LSTM network for sequence-to-label classification, create a layer array containing a sequence input layer, an LSTM layer, a fully connected layer, and a softmax layer.
Set the size of the sequence input layer to the number of features of the input data. Set the size of the fully connected layer to the number of classes. You do not need to specify the sequence length.
For the LSTM layer, specify the number of hidden units and the output mode "last".
numFeatures = 12; numHiddenUnits = 100; numClasses = 9; layers = [ ... sequenceInputLayer(numFeatures) lstmLayer(numHiddenUnits,OutputMode="last") fullyConnectedLayer(numClasses) softmaxLayer];
For an example showing how to train an LSTM network for sequence-to-label classification and classify new data, see Sequence Classification Using Deep Learning.
To create an LSTM network for sequence-to-sequence classification, use the same architecture as for sequence-to-label classification, but set the output mode of the LSTM layer to "sequence".
numFeatures = 12; numHiddenUnits = 100; numClasses = 9; layers = [ ... sequenceInputLayer(numFeatures) lstmLayer(numHiddenUnits,OutputMode="sequence") fullyConnectedLayer(numClasses) softmaxLayer];
Regression LSTM Networks
To create an LSTM network for sequence-to-one regression, create a layer array containing a sequence input layer, an LSTM layer, and a fully connected layer.
Set the size of the sequence input layer to the number of features of the input data. Set the size of the fully connected layer to the number of responses. You do not need to specify the sequence length.
For the LSTM layer, specify the number of hidden units and the output mode "last".
numFeatures = 12; numHiddenUnits = 125; numResponses = 1; layers = [ ... sequenceInputLayer(numFeatures) lstmLayer(numHiddenUnits,OutputMode="last") fullyConnectedLayer(numResponses)];
To create an LSTM network for sequence-to-sequence regression, use the same architecture as for sequence-to-one regression, but set the output mode of the LSTM layer to "sequence".
numFeatures = 12; numHiddenUnits = 125; numResponses = 1; layers = [ ... sequenceInputLayer(numFeatures) lstmLayer(numHiddenUnits,OutputMode="sequence") fullyConnectedLayer(numResponses)];
For an example showing how to train an LSTM network for sequence-to-sequence regression and predict on new data, see Sequence-to-Sequence Regression Using Deep Learning.
Deeper LSTM Networks
You can make LSTM networks deeper by inserting extra LSTM layers with the output mode "sequence" before the LSTM layer. To prevent overfitting, you can insert dropout layers after the LSTM layers.
For sequence-to-label classification networks, the output mode of the last LSTM layer must be "last".
numFeatures = 12; numHiddenUnits1 = 125; numHiddenUnits2 = 100; numClasses = 9; layers = [ ... sequenceInputLayer(numFeatures) lstmLayer(numHiddenUnits1,OutputMode="sequence") dropoutLayer(0.2) lstmLayer(numHiddenUnits2,OutputMode="last") dropoutLayer(0.2) fullyConnectedLayer(numClasses) softmaxLayer];
For sequence-to-sequence classification networks, the output mode of the last LSTM layer must be "sequence".
numFeatures = 12; numHiddenUnits1 = 125; numHiddenUnits2 = 100; numClasses = 9; layers = [ ... sequenceInputLayer(numFeatures) lstmLayer(numHiddenUnits1,OutputMode="sequence") dropoutLayer(0.2) lstmLayer(numHiddenUnits2,OutputMode="sequence") dropoutLayer(0.2) fullyConnectedLayer(numClasses) softmaxLayer];
Algorithms
Long Short-Term Memory Layer
An LSTM layer is an RNN layer that learns long-term dependencies between time steps in time-series and sequence data.
The state of the layer consists of the hidden state (also known as the output state) and the cell state. The hidden state at time step t contains the output of the LSTM layer for this time step. The cell state contains information learned from the previous time steps. At each time step, the layer adds information to or removes information from the cell state. The layer controls these updates using gates.
These components control the cell state and hidden state of the layer.
| Component | Purpose |
|---|---|
| Input gate (i) | Control level of cell state update |
| Forget gate (f) | Control level of cell state reset (forget) |
| Cell candidate (g) | Add information to cell state |
| Output gate (o) | Control level of cell state added to hidden state |
This diagram illustrates the flow of data at time step t. This diagram shows how the gates forget, update, and output the cell and hidden states.
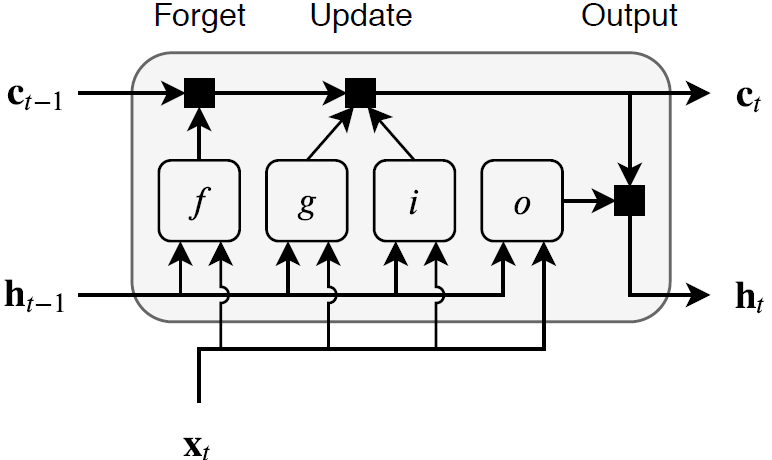
The learnable weights of an LSTM layer are the input weights W
(InputWeights), the recurrent weights R
(RecurrentWeights), and the bias b
(Bias). The matrices W, R,
and b are concatenations of the input weights, the recurrent weights, and
the bias of each component, respectively. The layer concatenates the matrices according to
these equations:
where i, f, g, and o denote the input gate, forget gate, cell candidate, and output gate, respectively.
The cell state at time step t is given by
where denotes the Hadamard product (element-wise multiplication of vectors).
The hidden state at time step t is given by
where denotes the state activation function. By default, the
lstmLayer function uses the hyperbolic tangent function (tanh) to
compute the state activation function.
These formulas describe the components at time step t.
| Component | Formula |
|---|---|
| Input gate | |
| Forget gate | |
| Cell candidate | |
| Output gate |
In these calculations, denotes the gate activation function. By default, the
lstmLayer function, uses the sigmoid function, given by , to compute the gate activation function.
Layer Input and Output Formats
Layers in a layer array or layer graph pass data to subsequent layers as formatted dlarray objects.
The format of a dlarray object is a string of characters, in which each
character describes the corresponding dimension of the data. The formats consist of one or
more of these characters:
"S"— Spatial"C"— Channel"B"— Batch"T"— Time"U"— Unspecified
For example, 2-D image data that is represented as a 4-D array, where the first two dimensions
correspond to the spatial dimensions of the images, the third dimension corresponds to the
channels of the images, and the fourth dimension corresponds to the batch dimension, can be
described as having the format "SSCB" (spatial, spatial, channel,
batch).
You can interact with these dlarray objects in automatic differentiation
workflows, such as those for developing a custom layer, using a functionLayer
object, or using the forward and predict functions with
dlnetwork objects.
This table shows the supported input formats of LSTMLayer objects and the
corresponding output format. If the software passes the output of the layer to a custom
layer that does not inherit from the nnet.layer.Formattable class, or a
FunctionLayer object with the Formattable property
set to 0 (false), then the layer receives an
unformatted dlarray object with dimensions ordered according to the formats
in this table. The formats listed here are only a subset. The layer may support additional
formats such as formats with additional "S" (spatial) or
"U" (unspecified) dimensions.
| Input Format | OutputMode | Output Format |
|---|---|---|
| "sequence" |
|
"last" | ||
| "sequence" |
|
"last" |
| |
| "sequence" |
|
"last" |
In dlnetwork objects, LSTMLayer objects also support these input and output format combinations.
| Input Format | OutputMode | Output Format |
|---|---|---|
| "sequence" |
|
"last" | ||
| "sequence" | |
"last" | ||
| "sequence" | |
"last" | ||
| "sequence" |
|
"last" |
| |
| "sequence" |
|
"last" |
| |
| "sequence" |
|
"last" |
| |
| "sequence" |
|
"last" | ||
| "sequence" | |
"last" | ||
| "sequence" | |
"last" | ||
| "sequence" |
|
"last" |
| |
| "sequence" |
|
"last" |
| |
| "sequence" |
|
"last" |
| |
| "sequence" |
|
"last" |
| |
| "sequence" |
|
"last" | ||
| "sequence" | |
"last" | ||
| "sequence" |
|
"last" |
| |
| "sequence" |
|
"last" |
| |
| "sequence" |
|
"last" |
| |
| "sequence" |
|
"last" |
|
If the HasStateInputs property is 1
(true), then the layer has two additional inputs with the names
"hidden" and "cell", which correspond to the
hidden state and cell state, respectively. These additional inputs expect input format
"CB" (channel, batch).
If the HasStateOutputs property is 1
(true), then the layer has two additional outputs with names
"hidden" and "cell", which correspond to the
hidden state and cell state, respectively. These additional outputs have output format
"CB" (channel, batch).
References
[1] Hochreiter, S, and J. Schmidhuber, 1997. Long short-term memory. Neural computation, 9(8), pp.1735–1780.
[2] Glorot, Xavier, and Yoshua Bengio. "Understanding the Difficulty of Training Deep Feedforward Neural Networks." In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, 249–356. Sardinia, Italy: AISTATS, 2010. https://proceedings.mlr.press/v9/glorot10a/glorot10a.pdf
[3] He, Kaiming, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. "Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification." In 2015 IEEE International Conference on Computer Vision (ICCV), 1026–34. Santiago, Chile: IEEE, 2015. https://doi.org/10.1109/ICCV.2015.123
[4] Saxe, Andrew M., James L. McClelland, and Surya Ganguli. "Exact Solutions to the Nonlinear Dynamics of Learning in Deep Linear Neural Networks.” Preprint, submitted February 19, 2014. https://arxiv.org/abs/1312.6120.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
Usage notes and limitations:
For code generation in general, the HasStateInputs and
HasStateOutputs properties must be set to
0 (false).
When generating code with Intel® MKL-DNN or ARM® Compute Library:
The
StateActivationFunctionproperty must be set to"tanh".The
GateActivationFunctionproperty must be set to"sigmoid".
GPU Code Generation
Generate CUDA® code for NVIDIA® GPUs using GPU Coder™.
Usage notes and limitations:
For GPU code generation, the
StateActivationFunctionproperty must be set to"tanh".For GPU code generation, the
GateActivationFunctionproperty must be set to"sigmoid".The
HasStateInputsandHasStateOutputsproperties must be set to0(false).
Version History
Introduced in R2017bR2024a: ReLU state activation function
To specify the ReLU state activation function, set the StateActivationFunction property to
"relu".
R2019a: Default input weights initialization is Glorot
Starting in R2019a, the software, by default, initializes the layer input weights of this layer using the Glorot initializer. This behavior helps stabilize training and usually reduces the training time of deep neural networks.
In previous releases, the software, by default, initializes the layer input weights using the
by sampling from a normal distribution with zero mean and variance 0.01. To reproduce this
behavior, set the InputWeightsInitializer option of the layer to
"narrow-normal".
R2019a: Default recurrent weights initialization is orthogonal
Starting in R2019a, the software, by default, initializes the layer recurrent weights of this layer with Q, the orthogonal matrix given by the QR decomposition of Z = QR for a random matrix Z sampled from a unit normal distribution. This behavior helps stabilize training and usually reduces the training time of deep neural networks.
In previous releases, the software, by default, initializes the layer recurrent weights using
the by sampling from a normal distribution with zero mean and variance 0.01. To
reproduce this behavior, set the RecurrentWeightsInitializer
option of the layer to "narrow-normal".
See Also
trainnet | trainingOptions | dlnetwork | sequenceInputLayer | bilstmLayer | gruLayer | convolution1dLayer | maxPooling1dLayer | averagePooling1dLayer | globalMaxPooling1dLayer | globalAveragePooling1dLayer | Deep Network
Designer
Topics
- Sequence Classification Using Deep Learning
- Sequence Classification Using 1-D Convolutions
- Time Series Forecasting Using Deep Learning
- Sequence-to-Sequence Classification Using Deep Learning
- Sequence-to-Sequence Regression Using Deep Learning
- Sequence-to-One Regression Using Deep Learning
- Classify Videos Using Deep Learning
- Long Short-Term Memory Neural Networks
- List of Deep Learning Layers
- Deep Learning Tips and Tricks
MATLAB 命令
您点击的链接对应于以下 MATLAB 命令:
请在 MATLAB 命令行窗口中直接输入以执行命令。Web 浏览器不支持 MATLAB 命令。

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)