zpklp2mb
Zero-pole-gain lowpass to M-band frequency transformation
Syntax
[Z2,P2,K2,AllpassNum,AllpassDen]
= zpklp2mb(Z,P,K,Wo,Wt)
[Z2,P2,K2,AllpassNum,AllpassDen]
= zpklp2mb(Z,P,K,Wo,Wt,Pass)
Description
[Z2,P2,K2,AllpassNum,AllpassDen]
= zpklp2mb(Z,P,K,Wo,Wt) returns zeros, Z2,
poles, P2, and gain factor, K2,
of the target filter transformed from the real lowpass prototype by
applying an Mth-order real lowpass to real multibandpass
frequency mapping. By default the DC feature is kept at its original
location.
[Z2,P2,K2,AllpassNum,AllpassDen]
= zpklp2mb(Z,P,K,Wo,Wt,Pass) allows you to specify an additional
parameter, Pass, which chooses between using the
“DC Mobility” and the "Nyquist Mobility". In the first
case the Nyquist feature stays at its original location and the DC
feature is free to move. In the second case the DC feature is kept
at an original frequency and the Nyquist feature is allowed to move.
It also returns the numerator, AllpassNum,
and the denominator, AllpassDen, of the allpass
mapping filter. The prototype lowpass filter is given with zeros, Z,
poles, P, and gain factor, K.
This transformation effectively places one feature of an original filter, located at frequency Wo, at the required target frequency locations, Wt1,...,WtM.
Relative positions of other features of an original filter do not change in the target filter. This means that it is possible to select two features of an original filter, F1 and F2, with F1 preceding F2. Feature F1 will still precede F2 after the transformation. However, the distance between F1 and F2 will not be the same before and after the transformation.
Choice of the feature subject to this transformation is not restricted to the cutoff frequency of an original lowpass filter. In general it is possible to select any feature; e.g., the stopband edge, the DC, the deep minimum in the stopband, or other ones.
This transformation can also be used for transforming other types of filters; e.g., notch filters or resonators can be easily replicated at a number of required frequency locations. A good application would be an adaptive tone cancellation circuit reacting to the changing number and location of tones.
Examples
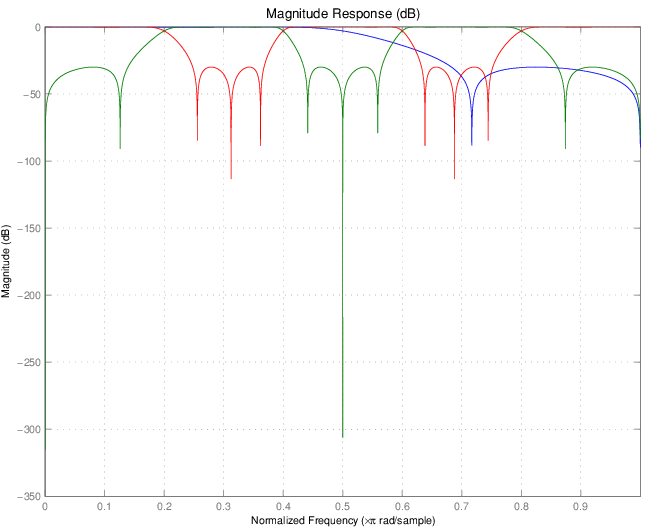
Design a prototype real IIR halfband filter using a standard elliptic approach:
[b, a] = ellip(3,0.1,30,0.409); z = roots(b); p = roots(a); k = b(1); [z1,p1,k1] = zpklp2mb(z, p, k, 0.5, [2 4 6 8]/10, 'pass'); [z2,p2,k2] = zpklp2mb(z, p, k, 0.5, [2 4 6 8]/10, 'stop');
Verify the result by comparing the prototype filter with the target filter:
filterAnalyzer(b,a,k1*poly(z1),poly(p1),k2*poly(z2),poly(p2),... FrequencyRange="onesided");
The resulting multiband filter that replicates features from the prototype appears in the figure shown. Note the accuracy of the replication process.
Arguments
| Variable | Description |
|---|---|
Z | Zeros of the prototype lowpass filter |
P | Poles of the prototype lowpass filter |
K | Gain factor of the prototype lowpass filter |
Wo | Frequency value to be transformed from the prototype filter |
Wt | Desired frequency location in the transformed target filter |
Pass | Choice ( |
Z2 | Zeros of the target filter |
P2 | Poles of the target filter |
K2 | Gain factor of the target filter |
AllpassNum | Numerator of the mapping filter |
AllpassDen | Denominator of the mapping filter |
Frequencies must be normalized to be between 0 and 1, with 1 corresponding to half the sample rate.
References
Franchitti, J.C., “All-pass filter interpolation and frequency transformation problems,” MSc Thesis, Dept. of Electrical and Computer Engineering, University of Colorado, 1985.
Feyh, G., J.C. Franchitti and C.T. Mullis, “All-pass filter interpolation and frequency transformation problem,” Proceedings 20th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, California, pp. 164-168, November 1986.
Mullis, C.T. and R.A. Roberts, Digital Signal Processing, section 6.7, Reading, Massachusetts, Addison-Wesley, 1987.
Feyh, G., W.B. Jones and C.T. Mullis, An extension of the Schur Algorithm for frequency transformations, Linear Circuits, Systems and Signal Processing: Theory and Application, C. J. Byrnes et al Eds, Amsterdam: Elsevier, 1988.
Version History
Introduced in R2011a