通过自适应滤波进行时滞通道估计
此示例说明如何使用 LMS 自适应 FIR 算法以自适应方式估计含噪输入信号的时滞。
假设有信号 ![$s[n] = a[n]+w[n]$](../../examples/dsp/win64/TimeDelayEstimationExample_eq06832886970054782519.png) ,其中
,其中 ![$w[n]$](../../examples/dsp/win64/TimeDelayEstimationExample_eq03178806122892290353.png) 是白高斯过程,且
是白高斯过程,且 ![$a[n]$](../../examples/dsp/win64/TimeDelayEstimationExample_eq00107744878115963933.png) 是确定性的。使用
是确定性的。使用 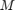 个采样的回声和衰减
个采样的回声和衰减  (两者均未知)测量该信号,得到整体测量:
(两者均未知)测量该信号,得到整体测量:
![$$ x[n] = s[n] + \alpha s[n-M] $$](../../examples/dsp/win64/TimeDelayEstimationExample_eq12097827341678758989.png)
目标是估计延迟 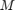 和回声衰减
和回声衰减  。您可以通过针对
。您可以通过针对 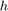 求解滤波器标识问题
求解滤波器标识问题 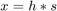 并结合先验
并结合先验 ![$h[n] = \delta[n]+\alpha s[n-M]$](../../examples/dsp/win64/TimeDelayEstimationExample_eq11860339517273811776.png) 来确定这些参数。只要可以从测量信号
来确定这些参数。只要可以从测量信号  和原始信号
和原始信号  标识出滤波器
标识出滤波器 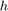 ,就可以推导
,就可以推导  和
和 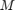
这样的滤波器标识问题可以用自适应 LTI 滤波来表示。参考信号是 ![$d[n] = x[n]$](../../examples/dsp/win64/TimeDelayEstimationExample_eq08782681346033574520.png) ,输入馈送是
,输入馈送是 ![$s[n]$](../../examples/dsp/win64/TimeDelayEstimationExample_eq03923724676957201790.png) ,自适应滤波器是
,自适应滤波器是 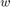 。显然,如果自适应过程以
。显然,如果自适应过程以 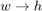 结束,则误差信号
结束,则误差信号 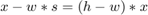 消失。
消失。
有许多自适应滤波算法。对于此特定问题设置和信号模型,归一化 LMS 算法是合适的,并该算法在 LMS Filter 模块中可用。
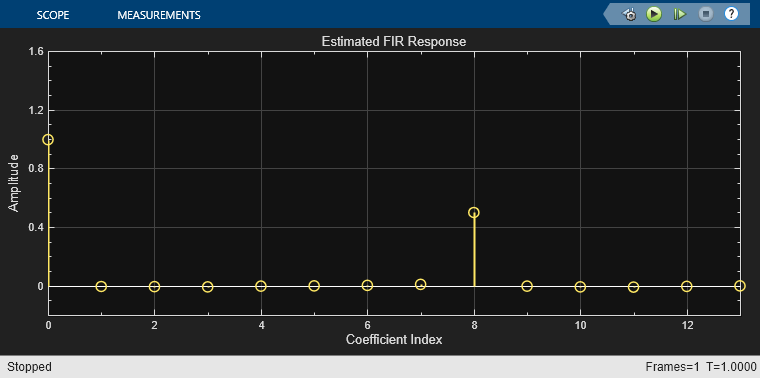
运行仿真。滤波器抽头向量中的峰值表示时滞估计值。在本例中,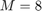 且
且 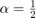 。
。
有关详细信息,请参阅 S. Haykin, Adaptive Filter Theory, 3rd Ed., Prentice-Hall 1996。