Estimate a Regression Model with Multiplicative ARIMA Errors

This example shows how to fit a regression model with multiplicative ARIMA errors to data using estimate.

Load the airline and recession data sets. Plot the monthly passenger totals and the log of the totals.

load Data_Airline
load Data_Recessions

y = DataTimeTable.PSSG;
logY = log(y);

figure
tiledlayout(2,1)
nexttile
plot(DataTimeTable.Time,y)
title('{\bf Monthly Passenger Totals (Jan1949 - Dec1960)}')
nexttile
plot(DataTimeTable.Time,log(y))
title('{\bf Monthly Passenger Log-Totals (Jan1949 - Dec1960)}')

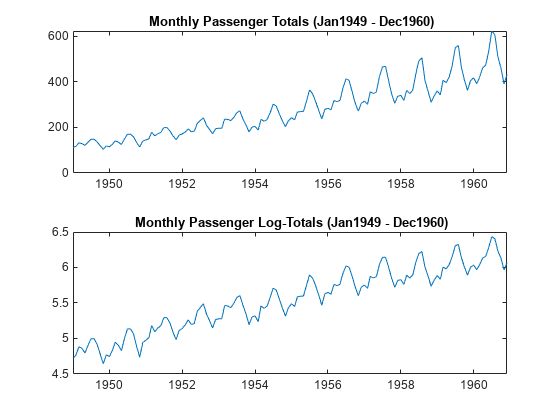
The log transformation seems to linearize the time series.

Construct the predictor (X), which is whether the country was in a recession during the sampled period. A 0 in row t means the country was not in a recession in month t, and a 1 in row t means that it was in a recession in month t.

X = zeros(numel(dates),1); % Preallocation
for j = 1:size(Recessions,1)
    X(dates >= Recessions(j,1) & dates <= Recessions(j,2)) = 1;
end

Fit the simple linear regression model

to the data.

EstMdl = fitlm(X,logY);

Fit is a LinearModel that contains the least squares estimates.

Check for standard linear model assumption departures by plotting the residuals several ways.

figure
tiledlayout(2,2)
nexttile
plotResiduals(EstMdl,'caseorder','ResidualType','Standardized',...
    'LineStyle','-','MarkerSize',0.5)
nexttile
plotResiduals(EstMdl,'lagged','ResidualType','Standardized')
nexttile
plotResiduals(EstMdl,'probability','ResidualType','Standardized')
nexttile
plotResiduals(EstMdl,'histogram','ResidualType','Standardized')

r = EstMdl.Residuals.Standardized;
figure
tiledlayout(2,1)
nexttile
autocorr(r)
nexttile
parcorr(r) 

The residual plots indicate that the unconditional disturbances are autocorrelated. The probability plot and histogram seem to indicate that the unconditional disturbances are Gaussian.

The ACF of the residuals confirms that the unconditional disturbances are autocorrelated.

Take the 1st difference of the residuals and plot the ACF and PACF of the differenced residuals.

dR = diff(r);

figure
tiledlayout(2,1)
nexttile
autocorr(dR,'NumLags',50)
nexttile
parcorr(dR,'NumLAgs',50)    

The ACF shows that there are significantly large autocorrelations, particularly at every 12th lag. This indicates that the unconditional disturbances have 12th degree seasonal integration.

Take the first and 12th differences of the residuals. Plot the differenced residuals, and their ACF and PACF.

DiffPoly = LagOp([1 -1]);
SDiffPoly = LagOp([1 -1],'Lags',[0, 12]);
diffR = filter(DiffPoly*SDiffPoly,r);

figure
tiledlayout("flow")
nexttile([1 2])
plot(diffR)
axis tight
nexttile
autocorr(diffR)
h = gca;
h.FontSize = 7;
nexttile
parcorr(diffR)
h = gca;
h.FontSize = 7;

The residuals resemble white noise (with possible heteroscedasticity). According to Box and Jenkins (1994), Chapter 9, the ACF and PACF indicate that the unconditional disturbances are an $$IMA(0,1,1)\times (0,1,1{)}_{12}$$ model.

Specify the regression model with $$IMA(0,1,1)\times (0,1,1{)}_{12}$$ errors:

Mdl = regARIMA('MALags',1,'D',1,'Seasonality',12,'SMALags',12)

Mdl = 
  regARIMA with properties:

     Description: "ARIMA(0,1,1) Error Model Seasonally Integrated with Seasonal MA(12) (Gaussian Distribution)"
      SeriesName: "Y"
    Distribution: Name = "Gaussian"
       Intercept: NaN
            Beta: [1×0]
               P: 13
               D: 1
               Q: 13
              AR: {}
             SAR: {}
              MA: {NaN} at lag [1]
             SMA: {NaN} at lag [12]
     Seasonality: 12
        Variance: NaN

Partition the data set into the presample and estimation sample so that you can initialize the series. P = Q = 13, so the presample should be at least 13 periods long.

preLogY = logY(1:13);   % Presample responses
estLogY = logY(14:end); % Estimation sample responses
preX = X(1:13);         % Presample predictors
estX = X(14:end);       % Estimation sample predictors

Obtain presample unconditional disturbances from a linear regression of the presample data.

PreFit = fitlm(preX,preLogY);...
    % Presample fit for presample residuals
EstFit = fitlm(estX,estLogY);...
    % Estimation sample fit for the intercept
U0 = PreFit.Residuals.Raw;

If the error model is integrated, then the regression model intercept is not identifiable. Set Intercept to the estimated intercept from a linear regression of the estimation sample data. Estimate the regression model with IMA errors.

Mdl.Intercept = EstFit.Coefficients{1,1};
EstMdl = estimate(Mdl,estLogY,'X',estX,'U0',U0);

 
    Regression with ARIMA(0,1,1) Error Model Seasonally Integrated with Seasonal MA(12) (Gaussian Distribution):
 
                   Value      StandardError    TStatistic      PValue  
                 _________    _____________    __________    __________

    Intercept       5.5722              0            Inf              0
    MA{1}        -0.025366        0.22197       -0.11427        0.90902
    SMA{12}       -0.80255       0.052705        -15.227     2.3349e-52
    Beta(1)      0.0027588        0.10139        0.02721        0.97829
    Variance     0.0072463     0.00015974         45.365              0

MA{1} and Beta1 are not significantly different from 0. You can remove these parameters from the model, possibly add other parameters (e.g., AR parameters), and compare multiple model fits using aicbic. Note that the estimation and presample should be the same over competing models.

References:

Box, G. E. P., G. M. Jenkins, and G. C. Reinsel. Time Series Analysis: Forecasting and Control. 3rd ed. Englewood Cliffs, NJ: Prentice Hall, 1994.

See Also

aicbic | regARIMA | estimate

Related Topics

• Maximum Likelihood Estimation of regARIMA Models
• Presample Values for regARIMA Model Estimation
• Intercept Identifiability in Regression Models with ARIMA Errors