Estimate Vector Error-Correction Model Using Econometric Modeler
This example models the annual Canadian inflation and interest rate series by using the Econometric Modeler app. The example shows how to perform the following actions in the app:
Test each raw series for stationarity.
Test for cointegration and determine a Johansen cointegration form if cointegration is present.
Fit several completing vector error-correction (VEC) models, and choose the one with the best, parsimonious fit.
Diagnose each residual series.
Export the chosen model to the command line.
At the command line, the example uses the model to generate forecasts.
The data set, which is stored in Data_Canada, contains annual
Canadian inflation and interest rates from 1954 through 1994.
Load and Import Data into Econometric Modeler
At the command line, load the Data_Canada.mat data
set.
load Data_CanadaAt the command line, open the Econometric Modeler app.
econometricModeler
Alternatively, open the app from the apps gallery (see Econometric Modeler).
Import DataTimeTable into the app:
On the Econometric Modeler tab, in the Import section, click the Import button
 .
.In the Import Data dialog box, in the Import? column, select the check box for the
DataTimeTablevariable.Click Import.
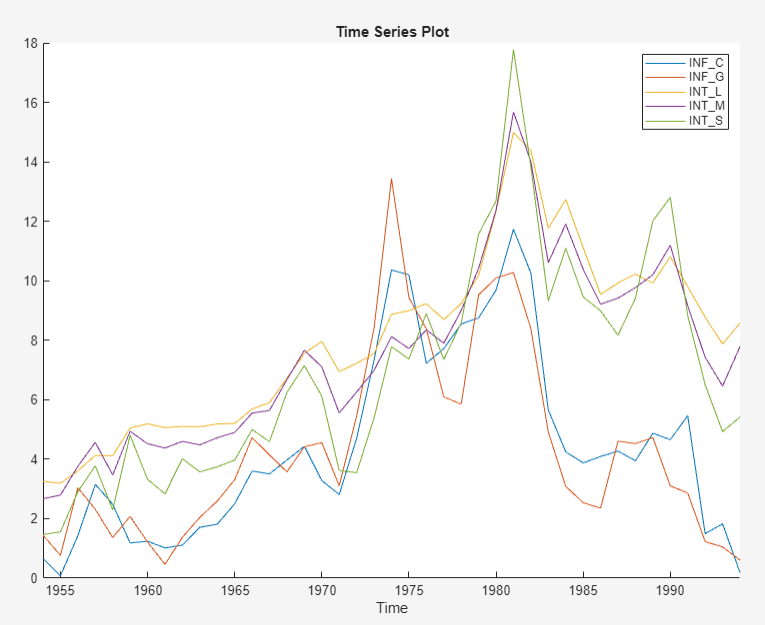
The Canadian interest and inflation rate variables appear in the Time Series pane, and a time series plot of all the series appears in the Time Series Plot(INF_C) figure window.
Plot only the three interest rate series INT_L,
INT_M, and INT_S
together. In the Time Series pane, click
INT_L and Ctrl+click
INT_M and INT_S. Then,
on the Plots tab, in the Plots
section, click Time Series. The time series plot
appears in the Time Series(INT_L) document.
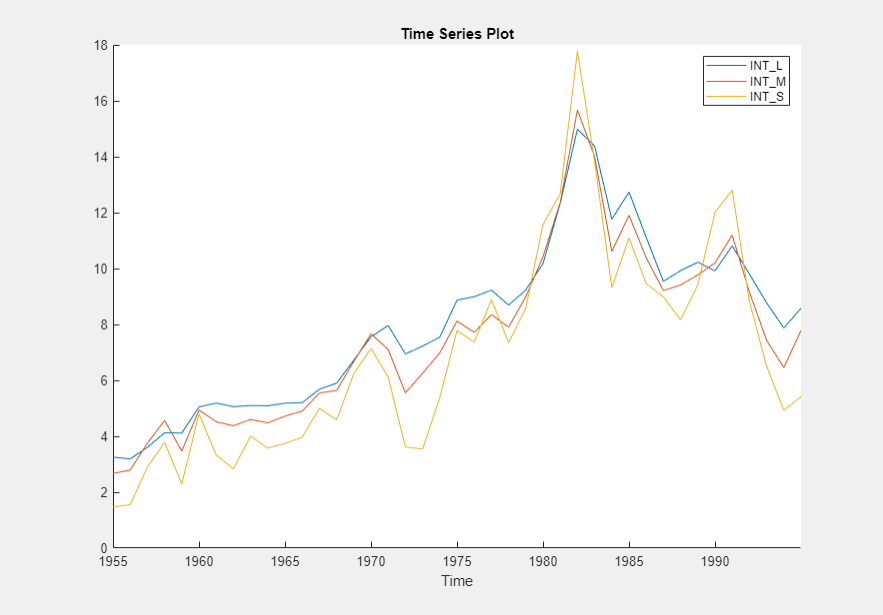
The interest rate series each appear nonstationary, and they appear to move together with mean-reverting spread. In other words, they exhibit cointegration. To establish these properties, this example conducts statistical tests.
Conduct Stationarity Test
Assess whether each interest rate series is stationary by conducting Phillips-Perron unit root tests. For each series, assume a stationary AR(1) process with drift for the alternative hypothesis. You can confirm this property by viewing the autocorrelation and partial autocorrelation function plots.
Close all plots in the right pane, and perform the following procedure for
each series INT_L, INT_M,
and INT_S.
In the Time Series pane, click a series.
On the Econometric Modeler tab, in the Tests section, click New Test > Phillips-Perron Test.
On the PP tab, in the Parameters section, in the Number of Lags box, type
1, and in the Model list select Autoregressive with Drift.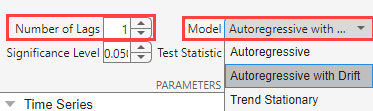
In the Tests section, click Run Test. Test results for the selected series appear in the PP(
series) tab.
Position the test results to view them simultaneously.
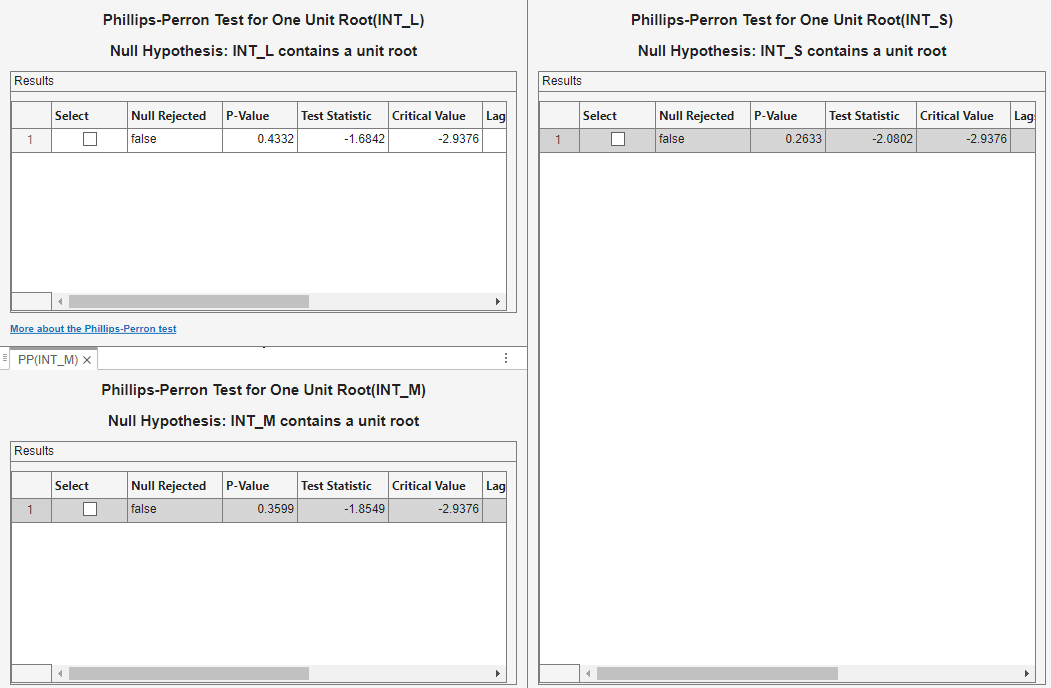
All tests fail to reject the null hypothesis that the series contains a unit root process.
Conduct Cointegration Test
To create and estimate a VEC model of unit root series, the series need to
exhibit cointegration. Conduct a Johansen test. Because the raw series do not
contain a linear trend, assume that the only deterministic term in the model is
an intercept in the cointegrating relation (H1*
Johansen form), and include 1 lagged difference term in the model.
In the Time Series pane, click
INT_Land Ctrl+clickINT_MandINT_S.In the Tests section, click New Test > Johansen Test.
On the JCI tab, in the Parameters section, in the Number of Lags box, type
1. In the Model list, select H1*.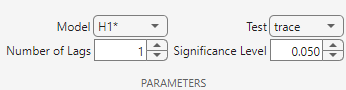
In the Tests section, click Run Test. Test results and a plot of the cointegration relation for the largest rank appear in the JCI tab.
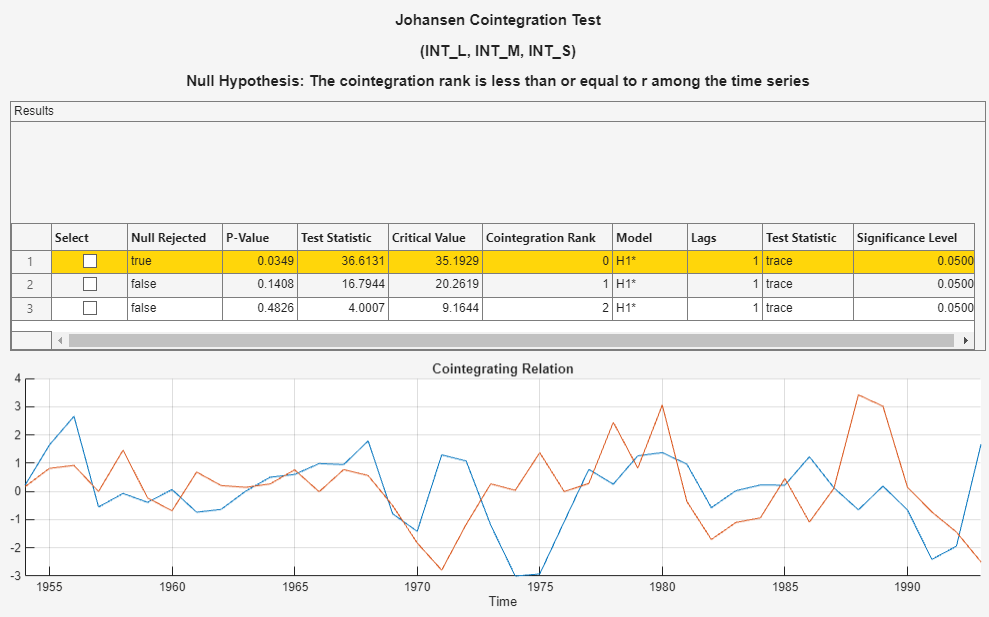
Econometric Modeler conducts a separate test for each cointegration rank 0 through 2 (the number of series – 1). The test rejects the null hypothesis of no cointegration (Cointegration rank = 0), but fails to reject the null hypothesis of Cointegration rank ≤ 1. The conclusion is to set the cointegration rank of the VEC model to 1.
Estimate VEC Models
Estimate 3-D VEC(p) models of the interest rate
series, with a cointegration rank of 1 and p = 1 and
2.
With
INT_L,INT_M, andINT_Sselected in the Time Series pane, in the Models section, click VEC.In the VEC Model Parameters dialog box, in the Johansen Form, select H1*. Fit the VEC(1) model by clicking Estimate.
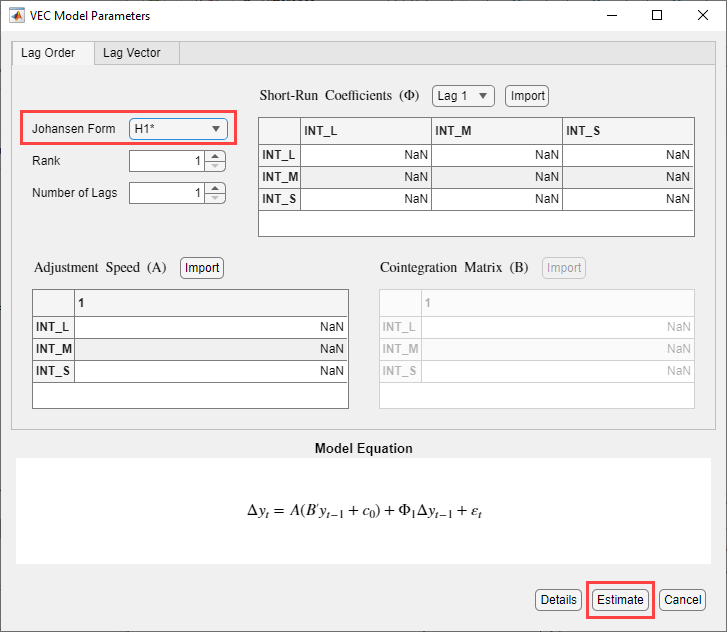
The model variable
VECappears in the Models pane, its value appears in the Preview pane, and its estimation summary appears in the Model Summary(VEC) document.Repeat steps 1 and 2 for the short-run polynomial order
p= 2.Similar to the VEC(1) estimation, the variable
VEC2appears in the Models pane, and its estimation summary appears in the Model Summary(VEC2) document. You can view properties of an estimated model in the Preview pane by clicking the model in the Models pane. For example, clickVEC.
Select Model with Best In-Sample Fit
The estimation summary in each Model
Summary(VECp) tab contains a plot
of fitted values and residuals, with respect to the time series in the
Time Series list, a standard statistical table of
estimates and inferences, and a table of information criteria.
Compare the information criteria of each estimated model simultaneously by positioning the estimation summary documents so that they occupy the left and right sections of the right pane. The model with the lowest value has the best, parsimonious fit.
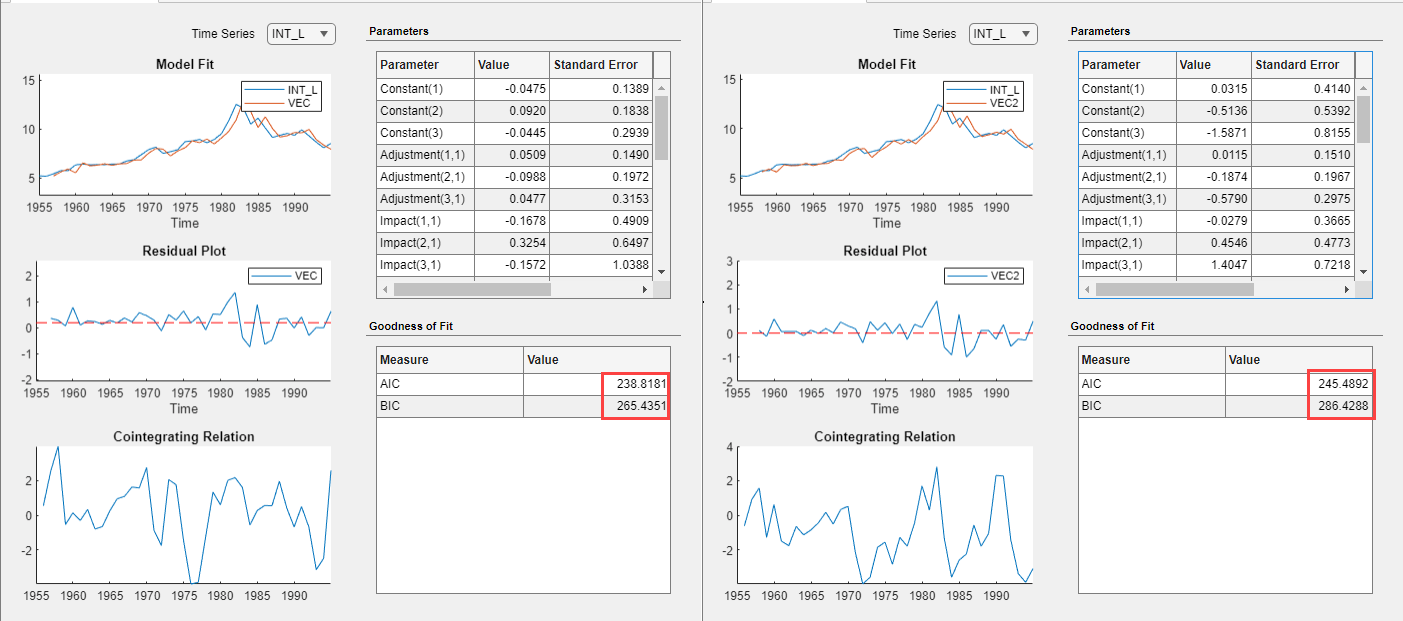
The VEC(1) model VEC produces the lowest AIC and
BIC values. Choose this model for further analysis.
Check Goodness of Fit
Inspect the following VEC(1) plots of each residual series:
Histograms, for center, normality, and outliers
Quantile-quantile plots, for normality, skewness, and tails
Autocorrelation function (ACF), for serial correlation
ACF of squared residual series, for heteroscedasticity
This example diagnoses the residuals visually. Alternatively, you can conduct statistical tests to diagnose the residuals.
Dismiss the Model Summary(VEC2) document by clicking ![]() on its tab.
on its tab.
On the Models pane, click
VEC.
Plot separate residual histograms. On the Econometric Modeler tab, in the Diagnostics section, click Residual Diagnostics > Residual Histogram. Histograms of the each residual series appear in the Histogram(VEC) document.
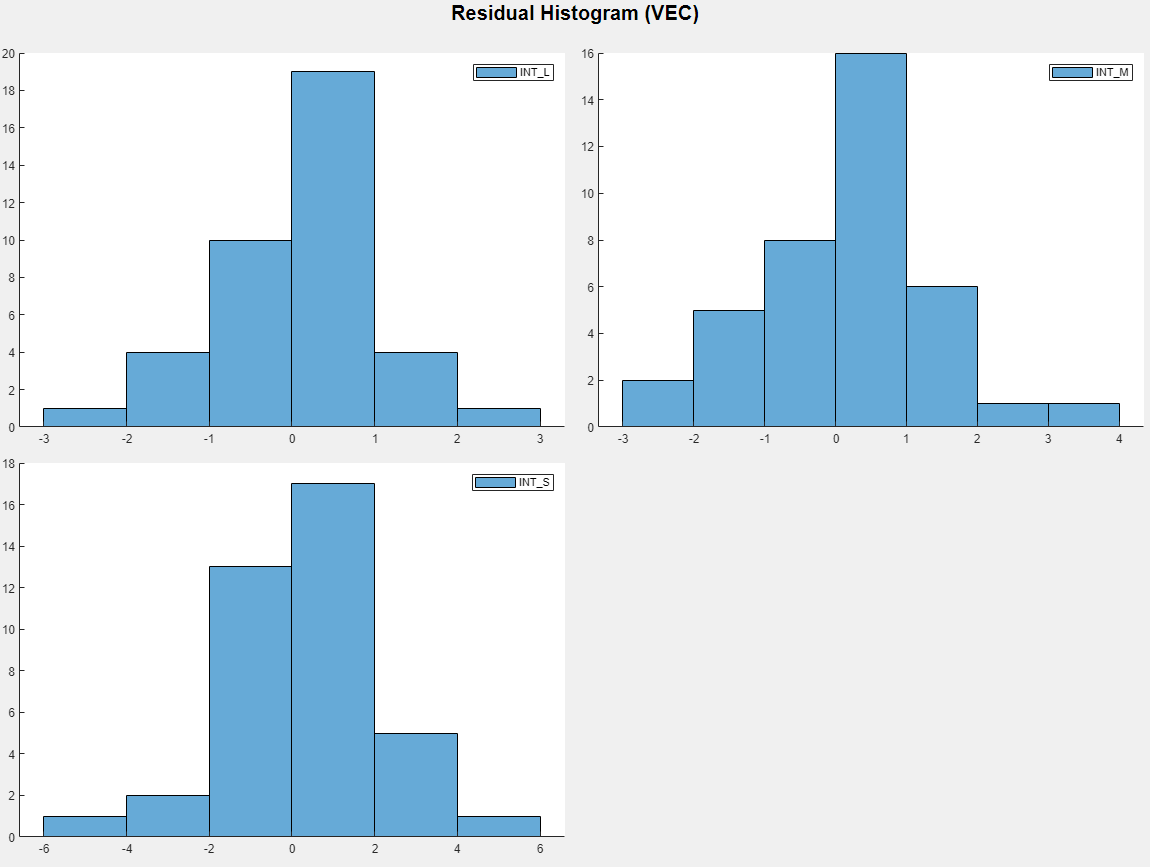
Each residual series appears approximately centered around 0 and approximately normal.
Plot separate residual quantile-quantile plots. With
VEC selected in the Time
Series pane, on the Econometric Modeler tab,
in the Diagnostics section, click Residual
Diagnostics > Residual Q-Q Plot.
Quantile-quantile plots of each residual series appear in the
QQPlot(VEC) document.
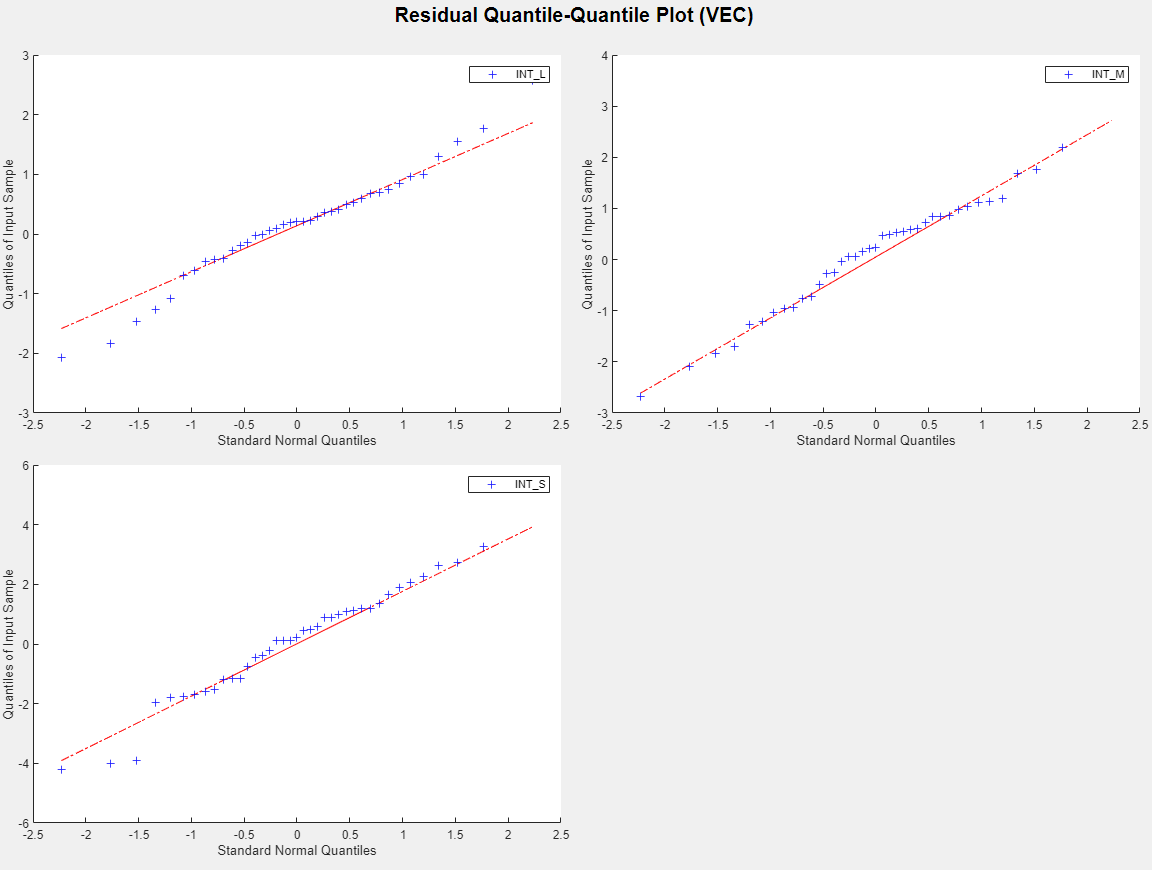
The residual series are slightly skewed left and have lighter tails than the normal distribution. This example proceeds without addressing possible skewness and light tails.
Plot separate ACF plots of each residual series. With
VEC selected in the Time
Series pane, on the Econometric Modeler tab,
in the Diagnostics section, click Residual
Diagnostics > Autocorrelation
Function. ACF plots of each residual series appear in the
ACF(VEC) document.

The residuals do not exhibit significant autocorrelation.
Plot separate ACF plots of each squared residual series. With
VEC selected in the Time
Series pane, on the Econometric Modeler tab,
in the Diagnostics section, click Residual
Diagnostics > Squared Residual
Autocorrelation. ACF plots of each squared residual series
appear in the ACF(VEC)2 document.

Each squared residual series has significant autocorrelations at early lags, which suggests that heteroscedasticity is present in all series. This example proceeds without addressing possible heteroscedasticity.
Export Model to Workspace
Export the model to the workspace.
With the
VECmodel selected in the Models pane, on the Econometric Modeler tab, in the Export section, click Export > Export Variables.In the Export Variables dialog box, select the Select check box for
INT_L,INT_M, andINT_S.Click Export.
The variables INT_L, INT_M,
INT_S, and VEC appear in the
workspace.
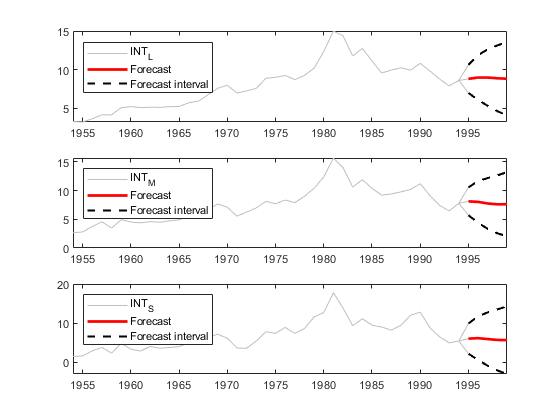
Generate Forecasts at Command Line
Generate forecasts and approximate 95% forecast intervals from the estimated
VEC(1) model for the next five years. For convenience, use the entire series as
a presample for the forecasts. The forecast function
discards all specified presample observations except for the required final
observation.
Y0 = [INT_L INT_M INT_S]; [YF,YFMSE] = forecast(VEC,5,Y0); YFSE = cell2mat(cellfun(@(x)sqrt(diag(x)'),YFMSE,UniformOutput=false)); UB = YF + 1.96*YFSE; LB = YF - 1.96*YFSE; datesF = DataTimeTable.Time(end) + calyears(1:5); figure tiledlayout(3,1) for j = 1:VEC.NumSeries nexttile h1 = plot(DataTimeTable.Time,Y0(:,j),Color=[.75,.75,.75]); hold on h2 = plot(datesF,YF(:,j),"r",LineWidth=2); h3 = plot(datesF,UB(:,j),"k--",LineWidth=1.5); plot(datesF,LB(:,j),"k--",LineWidth=1.5); ct = [Y0(end,j) YF(1,j); Y0(end,j) LB(1,j); Y0(end,j) UB(1,j);]; plot([DataTimeTable.Time(end); datesF(1)],ct,Color=[.75,.75,.75]) legend([h1 h2 h3],VEC.SeriesNames(j),"Forecast", ... "Forecast interval",Location="northwest") hold off end