Main Content

Pools with Different Numbers of Coupons Remaining

Suppose that one pool has two remaining coupons, and the other has three. MATLAB® expects the prepayment matrix to be in the following format:

V11       V21
V12       V22
NaN       V23

Vij denotes the single monthly mortality (SMM) rate for pool i during the jth coupon period since Settle.

The use of NaN to pad the prepayment matrix is necessary because MATLAB cannot concatenate vectors of different lengths into a matrix. Also, it can serve as an error check against any unintended operation (any MATLAB operation that would return NaN).

For example, assume that the 2-month pool has a constant SMM of 0.5% and the 3-month pool has a constant SMM of 1% in every period. The prepayment matrix you would create is depicted below.

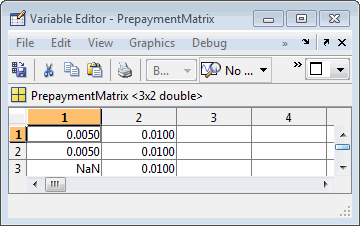
Variable editor displays prepayment matrix

Create this input in whatever manner is best for you.

Summary of Prepayment Data Vector Representation

  • When you specify a PSA prepayment speed, MATLAB "seasons" the pool according to its age.

  • When you specify your own prepayment matrix, identify the maximum number of coupons remaining using cpncount. Then supply the matrix elements up to the point when cash flow ceases to exist.

  • When different length pools must exist in the same matrix, pad the shorter one(s) with NaN. Each column of the prepayment matrix corresponds to a specific pool.

See Also

| | | | | | | | | | | | | | | | |

Related Examples

More About