Price Vanilla Instrument Using Heston Model and Multiple Different Pricers
This example shows the workflow to price a Vanilla instrument when you use a Heston model and various pricing methods.
Create Vanilla Instrument Object
Use fininstrument to create a Vanilla instrument object.
Settle = datetime(2017,6,29); Maturity = datemnth(Settle,6); Strike = 80; VanillaOpt = fininstrument('Vanilla','ExerciseDate',Maturity,'Strike',Strike,'Name',"vanilla_option")
VanillaOpt =
Vanilla with properties:
OptionType: "call"
ExerciseStyle: "european"
ExerciseDate: 29-Dec-2017
Strike: 80
Name: "vanilla_option"
Create Heston Model Object
Use finmodel to create a Heston model object.
V0 = 0.04; ThetaV = 0.05; Kappa = 1.0; SigmaV = 0.2; RhoSV = -0.7; HestonModel = finmodel("Heston",'V0',V0,'ThetaV',ThetaV,'Kappa',Kappa,'SigmaV',SigmaV,'RhoSV',RhoSV)
HestonModel =
Heston with properties:
V0: 0.0400
ThetaV: 0.0500
Kappa: 1
SigmaV: 0.2000
RhoSV: -0.7000
Create ratecurve object
Create a ratecurve object using ratecurve.
Rate = 0.03;
ZeroCurve = ratecurve('zero',Settle,Maturity,Rate);Create NumericalIntegration, FFT, and FiniteDifference Pricer Objects
Use finpricer to create a NumericalIntegration, FFT, and FiniteDifference pricer objects and use the ratecurve object for the 'DiscountCurve' name-value pair argument.
SpotPrice = 80; Strike = 80; DividendYield = 0.02; NIPricer = finpricer("NumericalIntegration",'Model', HestonModel,'SpotPrice',SpotPrice,'DiscountCurve',ZeroCurve,'DividendValue',DividendYield)
NIPricer =
NumericalIntegration with properties:
Model: [1×1 finmodel.Heston]
DiscountCurve: [1×1 ratecurve]
SpotPrice: 80
DividendType: "continuous"
DividendValue: 0.0200
AbsTol: 1.0000e-10
RelTol: 1.0000e-10
IntegrationRange: [1.0000e-09 Inf]
CharacteristicFcn: @characteristicFcnHeston
Framework: "heston1993"
VolRiskPremium: 0
LittleTrap: 1
FFTPricer = finpricer("FFT",'Model',HestonModel, ... 'SpotPrice',SpotPrice,'DiscountCurve',ZeroCurve, ... 'DividendValue',DividendYield,'NumFFT',8192)
FFTPricer =
FFT with properties:
Model: [1×1 finmodel.Heston]
DiscountCurve: [1×1 ratecurve]
SpotPrice: 80
DividendType: "continuous"
DividendValue: 0.0200
NumFFT: 8192
CharacteristicFcnStep: 0.0100
LogStrikeStep: 0.0767
CharacteristicFcn: @characteristicFcnHeston
DampingFactor: 1.5000
Quadrature: "simpson"
VolRiskPremium: 0
LittleTrap: 1
FDPricer = finpricer("FiniteDifference",'Model',HestonModel,'SpotPrice',SpotPrice,'DiscountCurve',ZeroCurve,'DividendValue',DividendYield)
FDPricer =
FiniteDifference with properties:
DiscountCurve: [1×1 ratecurve]
Model: [1×1 finmodel.Heston]
SpotPrice: 80
GridProperties: [1×1 struct]
DividendType: "continuous"
DividendValue: 0.0200
Price Vanilla Instrument
Use the following sensitivities when pricing the Vanilla instrument.
InpSensitivity = ["delta", "gamma", "theta", "rho", "vega", "vegalt"];
Use price to compute the price and sensitivities for the Vanilla instrument that uses the NumericalIntegration pricer.
[PriceNI, outPR_NI] = price(NIPricer,VanillaOpt,InpSensitivity)
PriceNI = 4.7007
outPR_NI =
priceresult with properties:
Results: [1×7 table]
PricerData: []
Use price to compute the price and sensitivities for the Vanilla instrument that uses the FFT pricer.
[PriceFFT, outPR_FFT] = price(FFTPricer,VanillaOpt,InpSensitivity)
PriceFFT = 4.7007
outPR_FFT =
priceresult with properties:
Results: [1×7 table]
PricerData: []
Use price to compute the price and sensitivities for the Vanilla instrument that uses the FiniteDifference pricer.
[PriceFD, outPR_FD] = price(FDPricer,VanillaOpt,InpSensitivity)
PriceFD = 4.7003
outPR_FD =
priceresult with properties:
Results: [1×7 table]
PricerData: [1×1 struct]
Aggregate the price results.
[outPR_NI.Results;outPR_FFT.Results;outPR_FD.Results]
ans=3×7 table
Price Delta Gamma Theta Rho Vega VegaLT
______ _______ ________ _______ ______ ______ ______
4.7007 0.57747 0.03392 -4.8474 20.805 17.028 5.2394
4.7007 0.57747 0.03392 -4.8474 20.805 17.028 5.2394
4.7003 0.57722 0.035254 -4.8483 20.801 17.046 5.2422
Compute Option Price Surfaces
Use the price function for the NumericalIntegration pricer and the price function for the FFT pricer to compute the prices for a range of Vanilla instruments.
Maturities = datemnth(Settle,(3:3:24)'); NumMaturities = length(Maturities); Strikes = (20:10:160)'; NumStrikes = length(Strikes); [Maturities_Full,Strikes_Full] = meshgrid(Maturities,Strikes); NumInst = numel(Strikes_Full); VanillaOptions(NumInst, 1) = fininstrument("vanilla", ... "ExerciseDate", Maturities_Full(1), "Strike", Strikes_Full(1)); for instidx=1:NumInst VanillaOptions(instidx) = fininstrument("vanilla", ... "ExerciseDate", Maturities_Full(instidx), "Strike", Strikes_Full(instidx)); end Prices_NI = price(NIPricer, VanillaOptions); Prices_FFT = price(FFTPricer, VanillaOptions); figure; surf(Maturities_Full,Strikes_Full,reshape(Prices_NI,[NumStrikes,NumMaturities])); title('Price (Numerical Integration)'); view(-112,34); xlabel('Maturity') ylabel('Strike')
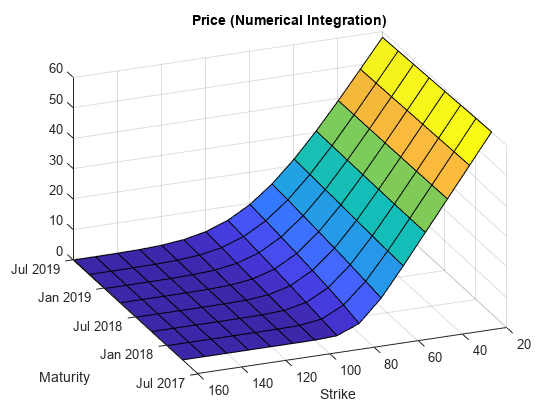
figure; surf(Maturities_Full,Strikes_Full,reshape(Prices_FFT,[NumStrikes,NumMaturities])); title('Price (FFT)'); view(-112,34); xlabel('Maturity') ylabel('Strike')
