算术运算
下列各节介绍哪些数据类型和定标选择项会导致溢出或精度损失。
模算术
二进制数学计算基于模算术。模算术仅使用有限数字集合,超出给定集合的任何计算结果会绕回到该集合。
例如,普通的日常钟表使用模 12 算术。此系统中的数字只能是 1 到 12。因此,在时钟系统中,9 加 9 等于 6。以数字环形式可以更直观地表示为如下:
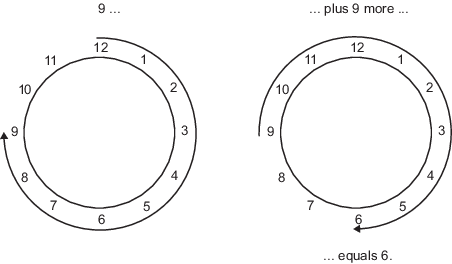
同样,二进制数学只能使用数字 0 和 1,超出此范围的任何算术结果都将以绕环形式绕回为 0 或 1。
2 的补码
2 的补码是解释二进制数字的一种方式。在 2 的补码中,正数始终以 0 开头,负数始终以 1 开头。如果 2 的补码数的前导位为 0,则通过计算该数的标准二进制值来获得该值。如果 2 的补码数的前导位是 1,则通过假设最左侧位是负数然后计算该数的二进制值来获得该值。例如,
要使用 2 的补码计算二进制数的负数,请执行下列操作:
获得 1 的补码,即翻转位。
按二进制数学计算方式加 2^(-FL),其中 FL 是小数长度。
丢弃超出原始字长的任何位。
以获得 11010 (-6) 的负数为例。首先,获得该数的 1 的补码:
接下来,加 1,将所有数字绕回为 0 或 1:
加减法
定点数的加法要求加数的二进制小数点对齐。然后使用二进制算术执行加法,不使用 0 或 1 以外的数字。
以将 010010.1 (18.5) 与 0110.110 (6.75) 相加为例:
定点减法相当于使用任何负值的 2 的补码值进行相加。在减法中,加数必须经过符号扩展以匹配彼此的长度。以从 010010.1 (18.5) 中减去 0110.110 (6.75) 为例:
在 Fixed-Point Designer™ 软件中,fimath 对象的 CastBeforeSum 属性具有默认值 1 (true)。这会在相加之前将加数转换为加和数据类型。因此,在相加过程中无需进一步移位来对齐二进制小数点。
如果 CastBeforeSum 属性的值为 0 (false),则加数相加时保持完整的精度。执行加法后,对和进行量化。
乘法
2 的补码定点数的乘法与普通小数乘法几乎完全一样,只是中间结果必须经过符号扩展,以便在它们相加之前将其左侧对齐。
以 10.11 (-1.25) 与 011 (3) 的乘法为例:

乘法数据类型
下图显示 Fixed-Point Designer 软件如何确定用于定点乘法的数据类型。这些图说明了实数与实数、复数与实数以及复数与复数之间乘法所用的数据类型之间的差异。
实数与实数的乘法. 下图显示在两个实数之间的乘法中 Fixed-Point Designer 软件使用的数据类型。此运算的输出以乘积数据类型返回,此数据类型由 fimath 对象的 ProductMode 属性确定。
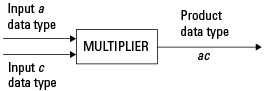
实数与复数之间的乘法. 下图显示在实数与复数定点数之间的乘法中 Fixed-Point Designer 软件使用的数据类型。实数与复数之间的乘法和复数与实数之间的乘法是等同的。软件以乘积数据类型返回此运算的输出,该数据类型由 fimath 对象的 ProductMode 属性确定:

复数与复数之间的乘法. 下图显示两个复数定点数的乘法。软件以加和数据类型返回此运算的输出,该数据类型由 fimath 对象的 SumMode 属性确定。中间乘积数据类型由 fimath 对象的 ProductMode 属性确定。
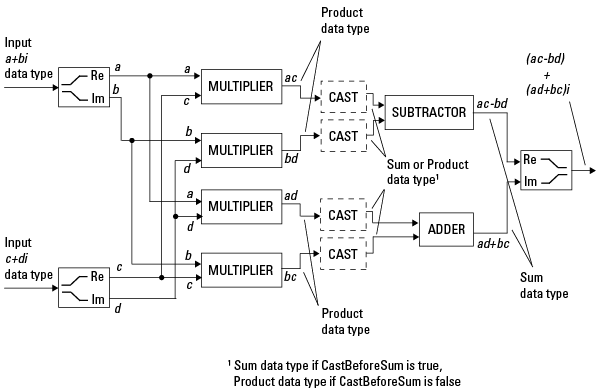
当 fimath 对象的 CastBeforeSum 属性为 true 时,在上图中的乘数后将转换为加和数据类型。在 C 代码中,对于减法器,这相当于
acc = ac; acc- = bd;
对于加法器,相当于
acc = ad; acc += bc;
其中 acc 是累加器。当 CastBeforeSum 属性为 false 时,转换不存在,并且在减法和加法运算之前数据仍为乘积数据类型。
与 fimath 对象相乘
以下示例说明 fimath 对象的 ProductMode 和 SumMode 属性如何影响实数和复数数据的乘法运算。
在以下示例中,基于如下条件:
F = fimath('ProductMode','FullPrecision',... 'SumMode','FullPrecision'); T1 = numerictype('WordLength',24,'FractionLength',20); T2 = numerictype('WordLength',16,'FractionLength',10); P = fipref; P.FimathDisplay = 'none';
实数与实数相乘. 将两个实数 x 和 y 相乘。请注意,结果 z 的字长和小数长度分别等于各被乘数的字长和小数长度之和。这是因为 fimath 对象的 ProductMode 和 SumMode 属性设置为 FullPrecision。
x = fi(5,T1,F) y = fi(10,T2,F) z = x*y
x =
5
DataTypeMode: Fixed-point: binary point scaling
Signedness: Signed
WordLength: 24
FractionLength: 20
y =
10
DataTypeMode: Fixed-point: binary point scaling
Signedness: Signed
WordLength: 16
FractionLength: 10
z =
50
DataTypeMode: Fixed-point: binary point scaling
Signedness: Signed
WordLength: 40
FractionLength: 30实数与复数相乘. 将实数 x 乘以复数 y。请注意,结果 z 的字长和小数长度分别等于各被乘数的字长和小数长度之和。这是因为 fimath 对象的 ProductMode 和 SumMode 属性设置为 FullPrecision。
x = fi(5,T1,F) y = fi(10+2i,T2,F) z = x*y
x =
5
DataTypeMode: Fixed-point: binary point scaling
Signedness: Signed
WordLength: 24
FractionLength: 20
y =
10.0000 + 2.0000i
DataTypeMode: Fixed-point: binary point scaling
Signedness: Signed
WordLength: 16
FractionLength: 10
z =
50.0000 +10.0000i
DataTypeMode: Fixed-point: binary point scaling
Signedness: Signed
WordLength: 40
FractionLength: 30复数与复数相乘. 将复数 x 乘以复数 y。复数与复数的乘法涉及加法和乘法。因此,全精度结果的字长比各被乘数的字长之和还要多一位。
x = fi(5+6i,T1,F) y = fi(10+2i,T2,F) z = x*y
x =
5.0000 + 6.0000i
DataTypeMode: Fixed-point: binary point scaling
Signedness: Signed
WordLength: 24
FractionLength: 20
y =
10.0000 + 2.0000i
DataTypeMode: Fixed-point: binary point scaling
Signedness: Signed
WordLength: 16
FractionLength: 10
z =
38.0000 +70.0000i
DataTypeMode: Fixed-point: binary point scaling
Signedness: Signed
WordLength: 41
FractionLength: 30转换
fimath 对象允许您使用 SumMode 和 ProductMode 属性指定中间总和与乘积的数据类型和定标。当您设置 SumMode 和 ProductMode 属性时,务必考虑每种转换会产生的影响。根据您选择的数据类型,可能会发生溢出和/或舍入。以下示例说明可能发生溢出和舍入的情况。有关转换的更多示例,请参阅Cast fi Objects。
从较短的数据类型转换为较长的数据类型
考虑将具有两个小数位的 4 位数据类型表示的非零数字转换为具有七个小数位的 8 位数据类型。

如上图所示,源位向上移位,以使二进制小数点与目标二进制小数点位置匹配。最高的源位无法容纳,因此可能会发生溢出,结果可能会进行饱和或绕回处理。目标数据类型低端的空位用 0 或 1 填充。
如果没有发生溢出,空位将用 0 填充。
如果发生绕回,空位将用 0 填充。
如果发生饱和,
正数的空位用 1 填充。
负数的空位用 0 填充。
即使从较短的数据类型转换为较长的数据类型,仍然可能发生溢出。当源数据类型的整数长度(本例中为 2)长于目标数据类型的整数长度(本例中为 1)时,会发生这种情况。同样,如果目标数据类型和定标的小数位小于源的小数位,则即使在从较短数据类型转换为较长数据类型时也可能需要舍入。
从较长的数据类型转换为较短的数据类型
考虑将具有七个小数位的 8 位数据类型表示的非零数字转换为具有两个小数位的 4 位数据类型。
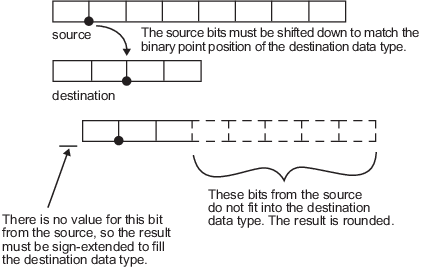
如上图所示,源位向下移位,以使二进制小数点与目标二进制小数点位置匹配。来自源的最高位没有值,因此使用符号扩展填充目标数据类型的整数部分。符号扩展是将具有最高有效位值的位加到 2 的补码数的高端。符号扩展不会更改二进制数的值。在此示例中,目标的小数长度不能容纳源的低端五位。因此,在对结果进行舍入后,精度可能会有一定丢失。
在这种情况下,即使转换是从较长数据类型到较短数据类型,所有整数位都会保留。相反,只要目标数据类型的小数长度等于或大于源数据类型的小数长度,即使转换为较短的数据类型,也可以保持全精度。但是,在这种情况下,结果的高端会丢失位并可能发生溢出。
当目标数据类型的整数长度和小数长度都短于源数据类型和定标的对应长度时,会出现最差情况。在这种情况下,会同时发生溢出和精度损失。