Create Lookup Tables for a Sine Function
Introduction
The sections that follow explain how to use the function fixpt_look1_func_approx to create lookup tables. It gives examples that show
how to create lookup tables for the function sin(2πx) on the interval from 0 to 0.25.
Set Function Parameters for the Lookup Table
First, define parameter values for the fixpt_look1_func_approx function.
% Required parameters funcstr = 'sin(2*pi*x)'; % Ideal function xmin = 0; % Minimum input of interest xmax = 0.25; % Maximum input of interest xdt = ufix(16); % x data type xscale = 2^-16; % x data scaling ydt = sfix(16); % y data type yscale = 2^-14; % y data scaling rndmeth = 'Floor'; % Rounding method % Optional parameters errmax = 2^-10; % Maximum allowed error of the lookup table nptsmax = 21; % Maximum number of points of the lookup table
The parameters errmax, nptsmax, and spacing are optional. You must use at least one of the parameters errmax and nptsmax. If you use only the errmax parameter without nptsmax, the function creates a lookup table with the fewest points for which the worst-case error is at most errmax. If you use only the nptsmax parameter without errmax, the function creates a lookup table with at most nptsmax points which has the smallest worst-case error. You can use the optional spacing parameter to restrict the spacing between breakpoints of the lookup table.
Use errmax with Unrestricted Spacing
Create a lookup table that has the fewest data points for a specified worst-case error, with unrestricted spacing.
[xdata,ydata,errworst] = fixpt_look1_func_approx(funcstr, ...
xmin,xmax,xdt,xscale,ydt,yscale,rndmeth,errmax,[]);Note that the nptsmax and spacing parameters are not specified.
length(xdata)
ans = 16
16 points are required to approximate to within the tolerance specified by errmax. The maximum error is:
errworst
errworst = 9.7656e-04
The value of errworst is less than or equal to the value of errmax.
Plot the results:
figure(1)
fixpt_look1_func_plot(xdata,ydata,funcstr,xmin,xmax,xdt, ...
xscale,ydt,yscale,rndmeth);
The upper plot shows the ideal function and the fixed-point lookup table approximation between the breakpoints. In this example, the ideal function and the approximation are so close together that the two graphs appear to coincide. The lower plot displays the errors.
In this example, the Y data points, ydata, are equal to the ideal function applied to the point in xdata. However, you can define a different set of values for ydata after running fixpt_look1_func_approx. This can sometimes reduce the maximum error.
You can also change the values of xmin and xmax to evaluate the lookup table on a subset of the original interval.
To find the new maximum error after changing ydata, xmin, or xmax, type
errworst = fixpt_look1_func_plot(xdata,ydata,funcstr,xmin,xmax,xdt,xscale,ydt,yscale,rndmeth)
Use nptsmax with Unrestricted Spacing
Create a lookup table that minimizes the worst-case error for a specified maximum number of data points, with unrestricted spacing.
[xdata, ydata, errworst] = fixpt_look1_func_approx(funcstr, ...
xmin,xmax,xdt,xscale,ydt,yscale,rndmeth,[],nptsmax);The empty brackets tell the function to ignore the parameter errmax. Omitting errmax causes the function to return a lookup table of size specified by nptsmax, with the smallest worst-case error.
length(xdata)
ans = 21
The function returns a vector xdata with 21 points. The maximum error is:
errworst
errworst = 5.1139e-04
The value of errworst is less than or equal to the value of errmax.
Plot the results:
figure(2)
fixpt_look1_func_plot(xdata,ydata,funcstr,xmin,xmax,xdt, ...
xscale,ydt,yscale,rndmeth);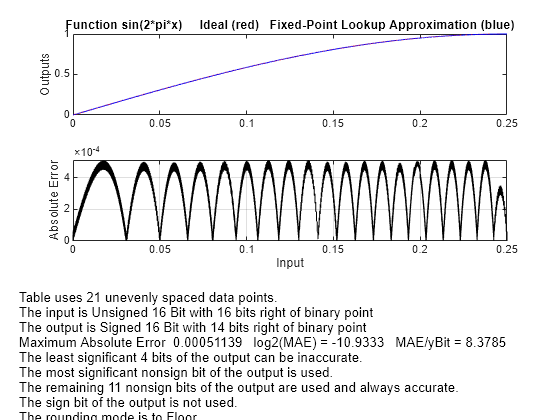
Restricting the Spacing
In the previous two examples, the function fixpt_look1_func_approx creates lookup tables with unrestricted spacing between the points. You can restrict the spacing to improve the computational efficiency of the lookup table using the spacing parameter. Both power of two, 'pow2', and even spacing, 'even', increase the computational speed of the lookup table and use less command read-only memory (ROM). However, specifying either of the spacing restrictions along with errmax usually requires more data points in the lookup table than does unrestricted spacing to achieve the same degree of accuracy. See Effects of Spacing on Speed, Error, and Memory Usage for more information.
Use errmax with Even Spacing
Create a lookup table that has evenly spaced breakpoints and a specified worst-case error.
spacing = 'even'; [xdata,ydata,errworst] = fixpt_look1_func_approx(funcstr, ... xmin,xmax,xdt,xscale,ydt,yscale,rndmeth,errmax,[],spacing); length(xdata)
ans = 20
errworst
errworst = 9.2109e-04
Plot the results:
figure(3)
fixpt_look1_func_plot(xdata,ydata,funcstr,xmin,xmax,xdt, ...
xscale,ydt,yscale,rndmeth);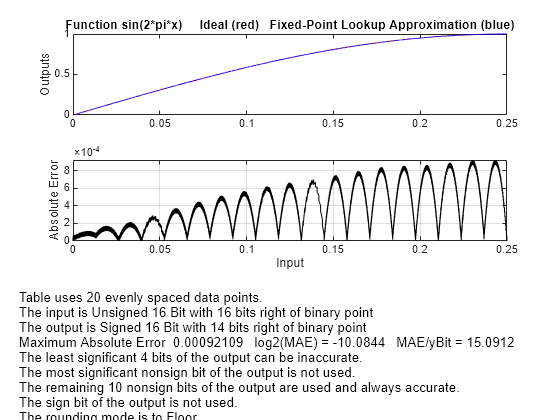
Use nptsmax with Even Spacing
Create a lookup table that has evenly spaced breakpoints and minimizes the worst-case error for a specified maximum number of points.
spacing = 'even'; [xdata, ydata, errworst] = fixpt_look1_func_approx(funcstr, ... xmin,xmax,xdt,xscale,ydt,yscale,rndmeth,[],nptsmax,spacing); length(xdata)
ans = 21
errworst
errworst = 8.3793e-04
The result requires 21 evenly spaced points to achieve a maximum absolute error of 2^-10.2209.
Plot the results:
figure(4)
fixpt_look1_func_plot(xdata,ydata,funcstr,xmin,xmax,xdt, ...
xscale,ydt,yscale,rndmeth);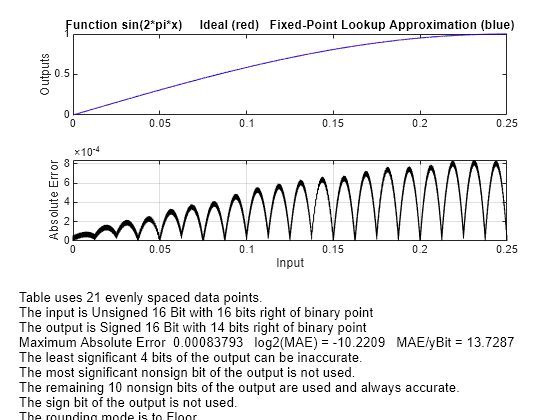
Use errmax with Power of Two Spacing
Create a lookup table that has power of two spacing and a specified worst-case error.
spacing = 'pow2'; [xdata, ydata, errworst] = ... fixpt_look1_func_approx(funcstr,xmin, ... xmax,xdt,xscale,ydt,yscale,rndmeth,errmax,[],spacing); length(xdata)
ans = 33
33 points are required to achieve the worst-case error specified by errmax. To verify that these points are evenly spaced, type
widths = diff(xdata)
widths = 32×1
0.0078
0.0078
0.0078
0.0078
0.0078
0.0078
0.0078
0.0078
0.0078
0.0078
0.0078
0.0078
0.0078
0.0078
0.0078
⋮
This generates a vector whose entries are the differences between the consecutive points in xdata. Every entry of widths is 2^-7.
The maximum error is:
errworst
errworst = 3.7209e-04
This is less than the value of errmax.
Plot the results:
figure(5)
fixpt_look1_func_plot(xdata,ydata,funcstr,xmin,xmax,xdt, ...
xscale,ydt,yscale,rndmeth);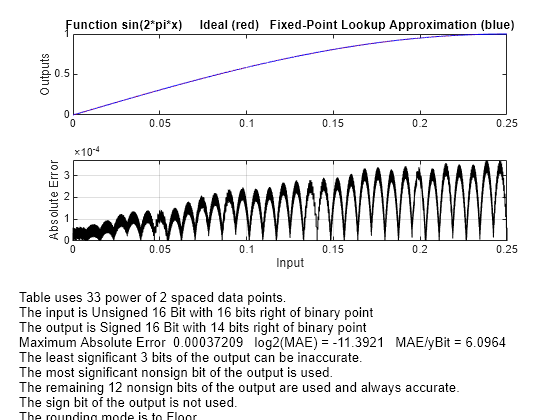
Use nptsmax with Power of Two Spacing
Create a lookup table that has power of two spacing and minimizes the worst-case error for a specified number of points.
spacing = 'pow2'; [xdata, ydata, errworst] = ... fixpt_look1_func_approx(funcstr,xmin, ... xmax,xdt,xscale,ydt,yscale,rndmeth,[],nptsmax,spacing); length(xdata)
ans = 17
errworst
errworst = 0.0013
The result requires 17 points to achieve a maximum absolute error of 2^-9.6267.
Plot the results:
figure(6)
fixpt_look1_func_plot(xdata,ydata,funcstr,xmin,xmax,xdt, ...
xscale,ydt,yscale,rndmeth);
Specifying Both errmax and nptsmax
If you include both the errmax and the nptsmax
parameters, the function fixpt_look1_func_approx tries to find a
lookup table with at most nptsmax data points, whose worst-case error is
at most errmax. If it can find a lookup table meeting both conditions, it
uses the following order of priority for spacing:
Power of two
Even
Unrestricted
If the function cannot find any lookup table satisfying both conditions, it ignores
nptsmax and returns a lookup table with unrestricted spacing, whose
worst-case error is at most errmax. In this case, the function behaves
the same as if the nptsmax parameter were omitted.
The following examples illustrate the results of using different values for
nptsmax when you enter
[xdata ydata errworst] = fixpt_look1_func_approx(funcstr, ... xmin,xmax,xdt,xscale,ydt,yscale,rndmeth,errmax,nptsmax);
The results for three different settings for nptsmax are as
follows:
nptsmax = 33;— The function creates the lookup table with 33 points having power of two spacing, as in Example 3.nptsmax = 21;— Because theerrmaxandnptsmaxconditions cannot be met with power of two spacing, the function creates the lookup table with 20 points having even spacing, as in Example 5.nptsmax = 16;— Because theerrmaxandnptsmaxconditions cannot be met with either power of two or even spacing, the function creates the lookup table with 16 points having unrestricted spacing, as in Example 1.
Comparison of Example Results
The following table summarizes the results for the examples. When you specify
errmax, even spacing requires more data points than unrestricted, and
power of two spacing requires more points than even spacing.
| Example | Options | Spacing | Worst-Case Error | Number of Points in Table |
|---|---|---|---|---|
1 |
|
|
| 16 |
2 |
|
|
| 21 |
3 |
|
|
| 20 |
4 |
|
|
| 21 |
5 |
|
|
| 33 |
6 |
|
|
| 17 |