Implement Hardware-Efficient Complex Partial-Systolic Q-less QR Decomposition

Economy Size Q-less QR Decomposition

The Complex Partial-Systolic Q-less QR Decomposition block performs the first step of solving the matrix equation A'AX = B which transforms A in-place to upper-triangular R, then solves the transformed system R'RX = B, where R'R = A'A.

Define Matrix Dimensions

Specify the number of rows and columns in matrix A.

m = 5;  % Number of rows in matrix A
n = 3;  % Number of columns in matrix A

Generate Matrix A

Use the helper function complexUniformRandomArray to generate a random matrix A such that the real and imaginary parts of the elements of A are between -1 and +1, and A is full rank.

rng('default')
A = fixed.example.complexUniformRandomArray(-1,1,m,n);

Select Fixed-Point Data Types

Use the helper function qlessqrFixedpointTypes to select fixed-point data types for matrix A that guarantee no overflow will occur in the transformation of A in-place to R.

The real and imaginary parts of the elements of A are between -1 and 1, so the maximum possible absolute value of any element is sqrt(2).

max_abs_A = sqrt(2);  % Upper bound on max(abs(A(:))
precisionBits = 24;   % Number of bits of precision
T = fixed.qlessqrFixedpointTypes(m,max_abs_A,precisionBits);
A = cast(A,'like',T.A);

Open the Model

model = 'ComplexPartialSystolicQlessQRModel';
open_system(model);

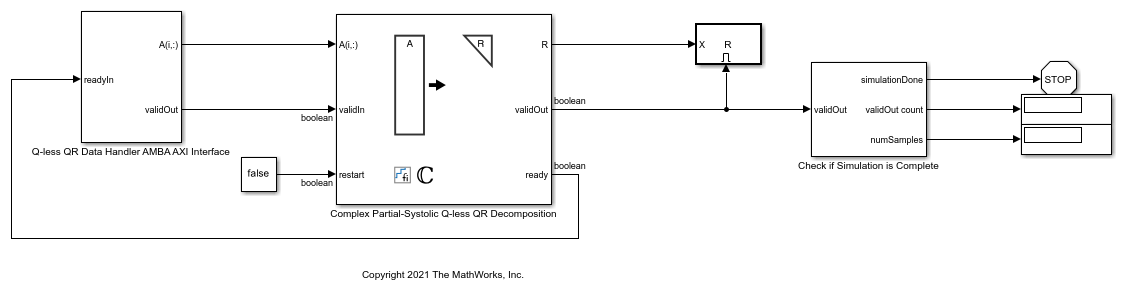
AMBA AXI Handshaking Process

The Data Handler subsystem in this model takes real matrix A as input. It sends rows of A to the QR Decomposition block using the AMBA AXI handshake protocol. The validIn signal indicates when data is available. The ready signal indicates that the block can accept the data. Transfer of data occurs only when both the validIn and ready signals are high. You can set delay for the feeding in rows of A in the Data Handler to emulate the processing time of the upstream block. validOut signal of the Data Handler remain high when rowDelay is set to 0 because this indicates the Data Handler always has data available.

Set Variables in the Model Workspace

Use the helper function setModelWorkspace to add the variables defined above to the model workspace. These variables correspond to the block parameters for the Complex Partial-Systolic Q-less QR Decomposition block.

numSamples = 1; % Number of sample matrices
rowDelay = 1; % Delay of clock cycles between feeding in rows of A
fixed.example.setModelWorkspace(model,'A',A,'m',m,'n',n,...
    'numSamples',numSamples,'rowDelay',rowDelay);

Simulate the Model

out = sim(model);

Construct the Solution from the Output Data

The Complex Partial-Systolic QR Decomposition block outputs matrix R at each time step. When a valid result matrix is output, the block sets validOut to true.

R = out.R;

R is an upper-triangular matrix.

R

R = 

   2.1863 + 0.0000i   0.6427 - 1.0882i  -0.5771 - 0.3089i
   0.0000 + 0.0000i   1.8126 + 0.0000i   0.2095 + 0.0599i
   0.0000 + 0.0000i   0.0000 + 0.0000i   1.7760 + 0.0000i

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 29
        FractionLength: 24

isequal(R,triu(R))

ans =

  logical

   1

Verify the Accuracy of the Output

To evaluate the accuracy of the Complex Partial-Systolic Q-less QR Decomposition block, compute the relative error.

relative_error = norm(double(R'*R - A'*A))/norm(double(A'*A))

relative_error =

   9.2898e-07

Suppress mlint warnings.

%#ok<*NOPTS>