Main Content

Propose Data Types Based on Simulation Ranges Using the fiaccel Function

This example shows how to propose fixed-point data types based on simulation range data using the fiaccel function.

Prerequisites

To complete this example, you must install the following products:

Create a New Folder and Copy Relevant Files

  1. In a local, writable folder, create a function ex_2ndOrder_filter.m.

    function y = ex_2ndOrder_filter(x) %#codegen
  persistent z
  if isempty(z)
      z = zeros(2,1);
  end
  % [b,a] = butter(2, 0.25)
  b = [0.0976310729378175,  0.195262145875635,  0.0976310729378175];
  a = [1, -0.942809041582063,  0.3333333333333333];

 
  y = zeros(size(x));
  for i = 1:length(x)
      y(i) = b(1)*x(i) + z(1);
      z(1) = b(2)*x(i) + z(2) - a(2) * y(i);
      z(2) = b(3)*x(i)        - a(3) * y(i);
  end
end

  2. Create a test file, ex_2ndOrder_filter_test.m, to exercise the ex_2ndOrder_filter algorithm.

    It is best practice to create a separate test script to do all the pre- and post-processing such as loading inputs, setting up input values, calling the function under test, and outputting test results.

    To cover the full intended operating range of the system, the test script runs the ex_2ndOrder_filter function with three input signals: chirp, step, and impulse. The script then plots the outputs.

    % ex_2ndOrder_filter_test
%
% Define representative inputs
N = 256;                   % Number of points
t = linspace(0,1,N);       % Time vector from 0 to 1 second
f1 = N/2;                  % Target frequency of chirp set to Nyquist
x_chirp = sin(pi*f1*t.^2); % Linear chirp from 0 to Fs/2 Hz in 1 second
x_step = ones(1,N);        % Step
x_impulse = zeros(1,N);    % Impulse
x_impulse(1) = 1;

% Run the function under test
x = [x_chirp;x_step;x_impulse];
y = zeros(size(x));
for i = 1:size(x,1)
  y(i,:) = ex_2ndOrder_filter(x(i,:));
end

% Plot the results
titles = {'Chirp','Step','Impulse'}
clf
for i = 1:size(x,1)
  subplot(size(x,1),1,i)
  plot(t,x(i,:),t,y(i,:))
  title(titles{i})
  legend('Input','Output')
end
xlabel('Time (s)')
figure(gcf)

disp('Test complete.')
TypeNameDescription
Function codeex_2ndOrder_filter.mEntry-point MATLAB function
Test fileex_2ndOrder_filter_test.mMATLAB script that tests ex_2ndOrder_filter.m

Set Up the Fixed-Point Configuration Object

Create a fixed-point configuration object and configure the test file name.

cfg = coder.config('fixpt');
cfg.TestBenchName = 'ex_2ndOrder_filter_test';

Collect Simulation Ranges and Generate Fixed-Point Code

Use the fiaccel function to convert the floating-point MATLAB function, ex_2ndOrder_filter, to fixed-point MATLAB code. Set the default word length for the fixed-point data types to 16.

cfg.ComputeSimulationRanges = true;
cfg.DefaultWordLength = 16;

% Derive ranges  and generate fixed-point code
fiaccel -float2fixed cfg ex_2ndOrder_filter

fiaccel analyzes the floating-point code. Because you did not specify the input types for the ex_2ndOrder_filter function, the conversion process infers types by simulating the test file. The conversion process then derives ranges for variables in the algorithm. It uses these derived ranges to propose fixed-point types for these variables. When the conversion is complete, it generates a type proposal report.

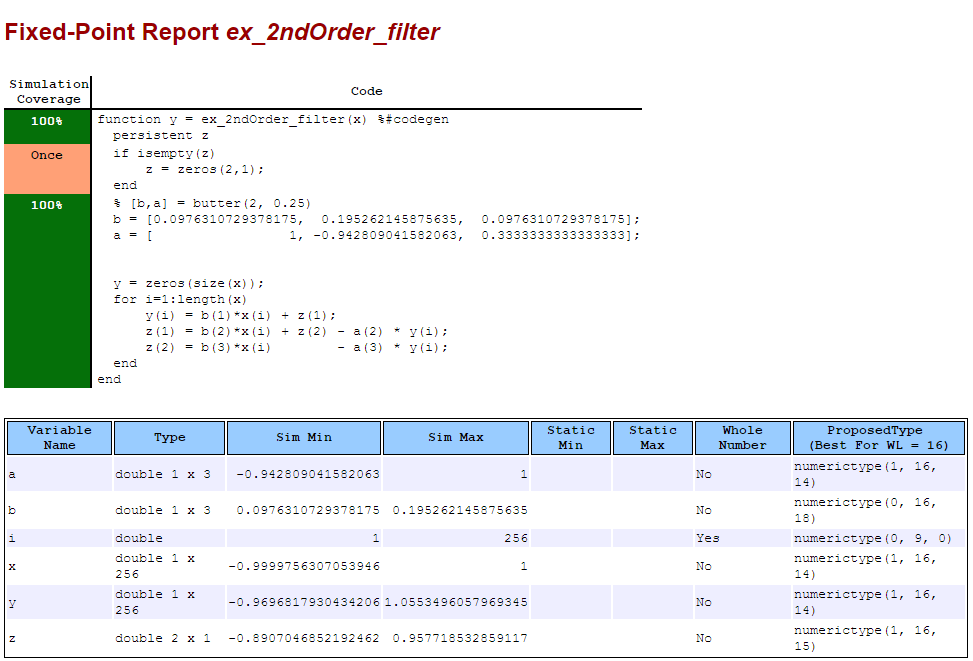
View Range Information

Click the link to the type proposal report for the ex_2ndOrder_filter function, ex_2ndOrder_filter_report.html.

The report opens in a web browser.

View Generated Fixed-Point MATLAB Code

fiaccel generates a fixed-point version of the ex_2ndOrder_filter.m function, ex_2ndOrder_filter_fixpt.m, and a wrapper function that calls ex_2ndOrder_filter_fixpt. These files are generated in the codegen\ex_2ndOrder_filter\fixpt folder in your local working folder.

function y = ex_2ndOrder_filter_fixpt(x) %#codegen
  fm = get_fimath();

  persistent z
  if isempty(z)
      z = fi(zeros(2,1),1,16,15,fm);
  end
  % [b,a] = butter(2, 0.25)
  b = fi([0.0976310729378175,0.195262145875635,0.0976310729378175],...
      0,16,18,fm);
  a = fi([1,-0.942809041582063,0.3333333333333333],1,16,14,fm);

 
  y = fi(zeros(size(x)),1,16,14,fm);
  for i=1:length(x)
      y(i) = b(1)*x(i) + z(1);
      z(1) = fi_signed(b(2)*x(i) + z(2)) - a(2) * y(i);
      z(2) = fi_signed(b(3)*x(i))        - a(3) * y(i);
  end
end



function y = fi_signed(a)
    coder.inline('always');
    if isfi(a) && ~(issigned(a))
        nt = numerictype(a);
        new_nt = numerictype(1,nt.WordLength + 1,...
            nt.FractionLength);
        y = fi(a,new_nt,fimath(a));
    else
        y = a;
    end
end

function fm = get_fimath()
	fm = fimath('RoundingMethod','Floor',...
        'OverflowAction','Wrap',...
        'ProductMode','FullPrecision',...
        'MaxProductWordLength',128,...
        'SumMode','FullPrecision',...
        'MaxSumWordLength',128);
end