量化

真实值 V 的量化 Q 由位的加权和表示。在一般的斜率和偏置编码方案的上下文中，无符号定点量的真实逼近值 $\tilde{V}$ 由下式给出：

$\tilde{V} = S \cdot [\sum_{i = 0}^{w s - 1} b_{i} 2^{i}] + B,$

而有符号定点量的真实逼近值由下式给出：

$\tilde{V} = S \cdot [- b_{w s - 1} 2^{w s - 1} + \sum_{i = 0}^{w s - 2} b_{i} 2^{i}] + B,$

其中

$b_{i}$ 是二进制位，其中 $b_{i} = 1, 0$ （对于 $i = 0, 1, ..., w s - 1$ ）
ws 是以位为单位的字长，其中 ws = 1、2、3、...、65535。
S 由 $S = F * 2^{E}$ 给出，其中定标是不受限制的，因为二进制小数点不必与字紧连。F 是斜率调整因子，它是在范围 [1.0, 2.0) 内的值。

$b_{i}$ 称为位乘数， $2^{i}$ 称为权重。

定点格式

8 位有符号和无符号定点值的格式如下图所示。

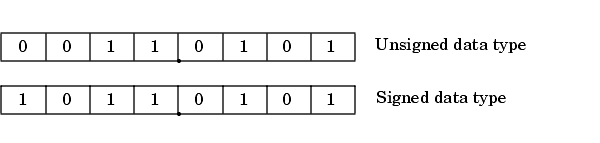
请注意，您无法仅通过检查来辨别这些数是有符号还是无符号数据类型，因为此信息未在字内显式编码。

二进制数 0011.0101 对无符号和 2 的补码表示产生相同的值，因为 MSB = 0。设置 B = 0 并使用适当的权重、位乘数和定标，该值为

$\begin{matrix} \tilde{V} = (F 2^{E}) Q = 2^{E} [\sum_{i = 0}^{w s - 1} b_{i} 2^{i}] \\ = 2^{- 4} (0 \times 2^{7} + 0 \times 2^{6} + 1 \times 2^{5} + 1 \times 2^{4} + 0 \times 2^{3} + 1 \times 2^{2} + 0 \times 2^{1} + 1 \times 2^{0}) \\ = 3.3125. \end{matrix}$

相反，二进制数 1011.0101 对无符号和 2 的补码表示产生不同的值，因为 MSB = 1。

设置 B = 0 并使用适当的权重、位乘数和定标，无符号值为

$\begin{matrix} \tilde{V} = (F 2^{E}) Q = 2^{E} [\sum_{i = 0}^{w s - 1} b_{i} 2^{i}] \\ = 2^{- 4} (1 \times 2^{7} + 0 \times 2^{6} + 1 \times 2^{5} + 1 \times 2^{4} + 0 \times 2^{3} + 1 \times 2^{2} + 0 \times 2^{1} + 1 \times 2^{0}) \\ = 11.3125, \end{matrix}$

而 2 的补码值为

$\begin{matrix} \tilde{V} = (F 2^{E}) Q = 2^{E} [- b_{w s - 1} 2^{w s - 1} + \sum_{i = 0}^{w s - 2} b_{i} 2^{i}] \\ = 2^{- 4} (- 1 \times 2^{7} + 0 \times 2^{6} + 1 \times 2^{5} + 1 \times 2^{4} + 0 \times 2^{3} + 1 \times 2^{2} + 0 \times 2^{1} + 1 \times 2^{0}) \\ = - 4.6875. \end{matrix}$

另请参阅

Simulink 中的定点数 | 定标