Fuzzy PID Control with Type-2 FIS

This example uses:

This example compares a type-2 fuzzy PID controller with both a type-1 fuzzy PID controller and conventional PID controller. This example is adapted from [1].

Fuzzy PID Control

This example uses the following fuzzy logic controller (FLC) structure as described in [1]. The controller is implemented using the Fuzzy PID Controller block. The output of the controller ( $u$ ) is found using the error ( $e$ ) and the derivative of the error ( $\dot{e}$ ). Using scaling factors $C_{e}$ and $C_{d}$ , inputs $e$ and $\dot{e}$ are normalized to $E$ and $Δ E$ , respectively. The normalized ranges for both inputs are in the range [-1,1]. The FLC also produces a normalized output in the range [-1,1]. Additional scaling factors $C_{0}$ and $C_{1}$ map the FLC output $U$ into $u$ .

This example uses a delayed first-order system $G (s)$ as the plant model.

$G (s) = \frac{C e^{- Ls}}{Ts + 1}$

Here, $C$ , $L$ , and $T$ are the gain, time delay, and time constant, respectively.

The scaling factors $C_{d}$ , $C_{0}$ , and $C_{1}$ are defined as follows, where $τ_{c}$ is the closed-loop time constant.

$\begin{array}{l} C_{d} = \min (T, \frac{L}{2}) \times C_{e} \\ C_{0} = \frac{1}{C \times C_{e} (τ_{c} + \frac{L}{2})} \\ C_{1} = \max (T, \frac{L}{2}) \times C_{0} \end{array}$

The input scaling factor $C_{e}$ is:

$C_{e} \equiv \frac{1}{r (t_{r}) - y (t_{r})}$

where $r (t_{r})$ and $y (t_{r})$ are the reference and system output values at time $t = t_{r}$ . These values correspond to the nominal operating point of the system.

This example compares the performance of type-1 and type-2 Sugeno fuzzy inference systems (FISs) using the Fuzzy PID Controller block.

Construct Type-1 FIS

Create a type-1 FIS using sugfis.

fis1 = sugfis;

Add input variables to the FIS.

fis1 = addInput(fis1,[-1 1],Name="E");
fis1 = addInput(fis1,[-1 1],Name="delE");

Add three uniformly distributed overlapping triangular membership functions (MFs) to each input. The MF names stand for negative (N), zero (Z), and positive (P).

fis1 = addMF(fis1,"E","trimf",[-2 -1 0],Name="N");
fis1 = addMF(fis1,"E","trimf",[-1 0 1],Name="Z");
fis1 = addMF(fis1,"E","trimf",[0 1 2],Name="P");
fis1 = addMF(fis1,"delE","trimf",[-2 -1 0],Name="N");
fis1 = addMF(fis1,"delE","trimf",[-1 0 1],Name="Z");
fis1 = addMF(fis1,"delE","trimf",[0 1 2],Name="P");

Plot the input membership functions.

figure
subplot(1,2,1)
plotmf(fis1,"input",1)
title("Input 1")
subplot(1,2,2)
plotmf(fis1,"input",2)
title("Input 2")

Figure contains 2 axes objects. Axes object 1 with title Input 1, xlabel E, ylabel Degree of membership contains 6 objects of type line, text. Axes object 2 with title Input 2, xlabel delE, ylabel Degree of membership contains 6 objects of type line, text.

Add the output variable to the FIS.

fis1 = addOutput(fis1,[-1 1],Name="U");

Add uniformly distributed constant functions to the output. The MF names stand for negative big (NB), negative medium (NM), zero (Z), positive medium (PM), and positive big (PB).

fis1 = addMF(fis1,"U","constant",-1,Name="NB");
fis1 = addMF(fis1,"U","constant",-0.5,Name="NM");
fis1 = addMF(fis1,"U","constant",0,Name="Z");
fis1 = addMF(fis1,"U","constant",0.5,Name="PM");
fis1 = addMF(fis1,"U","constant",1,Name="PB");

Add rules to the FIS. These rules create a proportional control surface.

rules = [...
    "E==N & delE==N => U=NB"; ...
    "E==Z & delE==N => U=NM"; ...
    "E==P & delE==N => U=Z"; ...
    "E==N & delE==Z => U=NM"; ...
    "E==Z & delE==Z => U=Z"; ...
    "E==P & delE==Z => U=PM"; ...
    "E==N & delE==P => U=Z"; ...
    "E==Z & delE==P => U=PM"; ...
    "E==P & delE==P => U=PB" ...
    ];
fis1 = addRule(fis1,rules);

Plot the control surface.

figure
gensurf(fis1)
title("Control surface of type-1 FIS")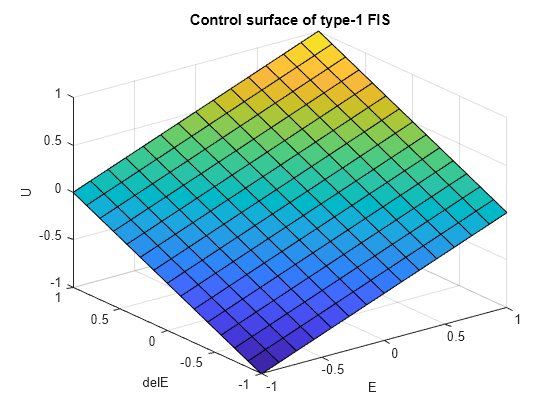

Figure contains an axes object. The axes object with title Control surface of type-1 FIS, xlabel E, ylabel delE contains an object of type surface.

You can also load the fuzzy inference system from type1FuzzyController.fis.

fis1 = readfis("type1FuzzyController.fis");

Construct Type-2 FIS

Convert the type-1 FIS, fis1, to a type-2 FIS.

fis2 = convertToType2(fis1);

The type-2 Sugeno system, fis2, uses type-2 membership functions for the input variables and type-1 membership functions for the output variables.

Define the footprint of uncertainty (FOU) for the input MFs as defined in [1]. To do so, set the lower MF scaling factor for each MF. For this example, set the lower MF lag values to 0.

scale = [0.2 0.9 0.2;0.3 0.9 0.3];
for i = 1:length(fis2.Inputs)
    for j = 1:length(fis2.Inputs(i).MembershipFunctions)
        fis2.Inputs(i).MembershipFunctions(j).LowerLag = 0;
        fis2.Inputs(i).MembershipFunctions(j).LowerScale = scale(i,j);
    end
end

Plot the type-2 input membership functions.

figure
subplot(1,2,1)
plotmf(fis2,"input",1)
title("Input 1")
subplot(1,2,2)
plotmf(fis2,"input",2)
title("Input 2")

Figure contains 2 axes objects. Axes object 1 with title Input 1, xlabel E, ylabel Degree of membership contains 12 objects of type line, patch, text. These objects represent UpperMF, LowerMF, FOU. Axes object 2 with title Input 2, xlabel delE, ylabel Degree of membership contains 12 objects of type line, patch, text. These objects represent UpperMF, LowerMF, FOU.

You can also load the fuzzy inference system from type2FuzzyController.fis.

fis2 = readfis("type2FuzzyController.fis");

The FOU adds additional uncertainty to the FIS and produces a nonlinear control surface.

figure
gensurf(fis2)
title("Control surface of type-2 FIS")

Figure contains an axes object. The axes object with title Control surface of type-2 FIS, xlabel E, ylabel delE contains an object of type surface.

Conventional PID Controller

This example compares the FLC performance with that of the following conventional PID controller.

$PID (s) = K_{p} + \frac{K_{i}}{s} + \frac{K_{d} s}{τ_{f} s + 1}$

Here, $K_{p}$ is proportional gain, $K_{i}$ is integrator gain, $K_{d}$ is derivative gain, and $τ_{f}$ is the derivative filter time constant.

Configure Simulation

Define the nominal plant model.

C = 0.5;
L = 0.5;
T = 0.5;
G = tf(C,[T 1],"Outputdelay",L);

Generate the conventional PID controller parameters using pidtune.

pidController = pidtune(G,"pidf");

In this example, the reference ( $r)$ is a step signal and $t_{r} = 0$ , which results in $C_{e} = 1$ as follows.

$C_{e} = \frac{1}{r (t_{r}) - y (t_{r})} = \frac{1}{1 - 0}$ =1.

Ce = 1;

To configure the simulation, use the following nominal controller parameters.

tauC = 0.2;

Cd = min(T,L/2)*Ce;
C0 = 1/(C*Ce*(tauC+L/2));
C1 = max(T,L/2)*C0;

To simulate the controllers, use the comparepidcontrollers Simulink model.

model = "comparepidcontrollers";
load_system(model)

Simulate Nominal Process

Simulate the model at the nominal operating conditions.

out1 = sim(model);

Plot the step response of the system for all three controllers.

plotOutput(out1,"Nominal",C,L,T)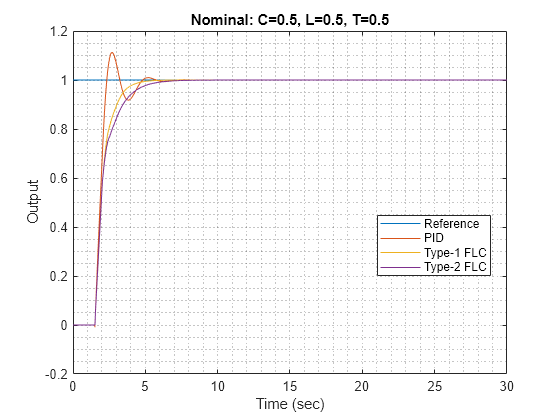

Figure contains an axes object. The axes object with title Nominal: C=0.5, L=0.5, T=0.5, xlabel Time (sec), ylabel Output contains 4 objects of type line. These objects represent Reference, PID, Type-1 FLC, Type-2 FLC.

Obtain the step-response characteristics of the system for each controller. Here, rise time and settling time are in seconds, overshoot is a percentage of the final value, and the absolute error is integrated over the step response.

stepResponseTable(out1)

ans=3×4 table
                  Rise Time    Overshoot    Settling Time    Absolute Error
                  _________    _________    _____________    ______________

    PID            0.62412      11.234         4.5583              1.04    
    Type-1 FLC      1.4353           0         4.1172            1.1552    
    Type-2 FLC      1.8582           0         5.1278             1.279

For the nominal process:

Both the type-1 and type-2 FLCs outperform the conventional PID controller in terms of overshoot.
The conventional PID controller, performs better with respect to rise-time and integral of absolute error (IAE).
The type-1 FLC performs better than the type-2 FLC in terms of rise-time, settling-time, and IAE.

Simulate Modified Process

Modify the plant model by increasing the gain, time delay, and time constant values as compared to the nominal process.

C = 0.85;
L = 0.6;
T = 0.6;
G = tf(C,[T 1],"Outputdelay",L);

Simulate the model using the updated plant parameters.

out2 = sim(model);

Plot the step response of the system for all three controllers.

plotOutput(out2,"Modified 1",C,L,T)

Figure contains an axes object. The axes object with title Modified 1: C=0.85, L=0.6, T=0.6, xlabel Time (sec), ylabel Output contains 4 objects of type line. These objects represent Reference, PID, Type-1 FLC, Type-2 FLC.

Obtain the step-response characteristics of the system for each controller.

stepResponseTable(out2)

ans=3×4 table
                  Rise Time    Overshoot    Settling Time    Absolute Error
                  _________    _________    _____________    ______________

    PID            0.38464      80.641         29.458            4.7486    
    Type-1 FLC     0.47241      25.555         4.7309            1.1309    
    Type-2 FLC     0.47209      23.958         3.4148            1.0851

For this modified process:

The conventional PID controller exhibits significant overshoot, larger settling-time, and higher IAE as compared to the fuzzy lFLCs
For all performance measures, the type-2 FLC produces the same or superior performance compared to the type-1 FLC.

Conclusion

Overall, the type-1 FLC produces superior performance for the nominal plant as compared to the conventional PID controller. The type-2 FLC shows more robust performance for the modified plant.

The robustness of the conventional PID controller can be improved using different methods, such as prediction or multiple PID controller configurations. On the other hand, the performance of a type-2 FLC can be improved by using a different:

Rule base
Number of rules
FOU

For example, you can create a type-2 FLC that defines the FOU using both the lower MF scaling factor and lower MF lag.

For fis2, set the lower MF scale and lag values to 0.7 and 0.1, respectively for all input membership functions.

for i = 1:length(fis2.Inputs)
    for j = 1:length(fis2.Inputs(i).MembershipFunctions)
        fis2.Inputs(i).MembershipFunctions(j).LowerScale = 0.7;
        fis2.Inputs(i).MembershipFunctions(j).LowerLag = 0.1;
    end
end

Plot the updated membership functions.

figure
subplot(1,2,1)
plotmf(fis2,"input",1)
title("Input 1")
subplot(1,2,2)
plotmf(fis2,"input",2)
title("Input 2")

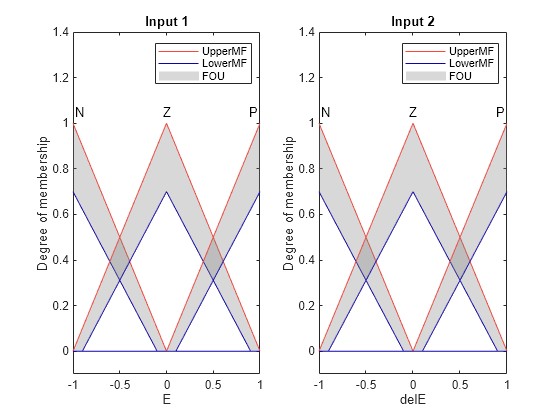
Simulate the model using the nominal plant, and plot the step responses for the controllers.

C = 0.5;
L = 0.5;
T = 0.5;
G = tf(C,[T 1],"Outputdelay",L);

out4 = sim(model);
plotOutput(out4,"Nominal",C,L,T)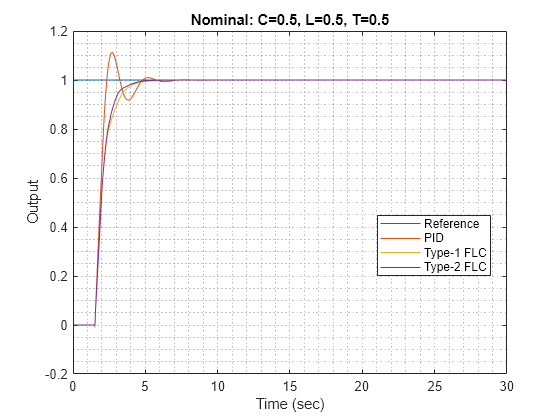

Obtain the step-response characteristics of the system for each controller.

stepResponseTable(out4)

ans=3×4 table
                  Rise Time    Overshoot    Settling Time    Absolute Error
                  _________    _________    _____________    ______________

    PID            0.62412      11.234         4.5583              1.04    
    Type-1 FLC      1.4353           0         4.1172            1.1552    
    Type-2 FLC      1.2233           0         3.9064            1.1126

In this case, the updated FOU of type-2 FLC improves the rise-time of the step response.

However, the lower MF lag values also increase the overshoot in the case of the modified plant.

C = 0.85;
L = 0.6;
T = 0.6;
G = tf(C,[T 1],"Outputdelay",L);

out5 = sim(model);
plotOutput(out5,"Modified",C,L,T)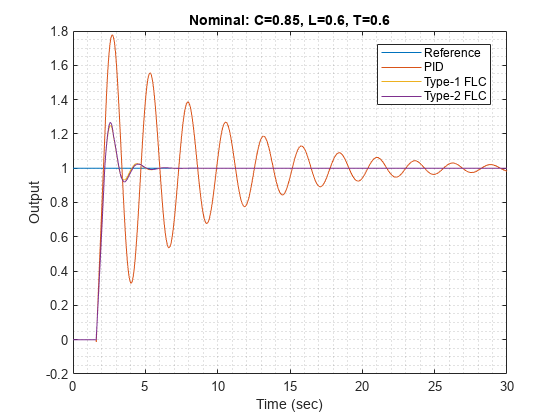

Figure contains an axes object. The axes object with title Modified: C=0.85, L=0.6, T=0.6, xlabel Time (sec), ylabel Output contains 4 objects of type line. These objects represent Reference, PID, Type-1 FLC, Type-2 FLC.

t = stepResponseTable(out5)

t=3×4 table
                  Rise Time    Overshoot    Settling Time    Absolute Error
                  _________    _________    _____________    ______________

    PID            0.38464      80.641         29.458            4.7486    
    Type-1 FLC     0.47241      25.555         4.7309            1.1309    
    Type-2 FLC     0.47241      27.398         4.7273            1.1427

Therefore, to obtain desired step response characteristics, you can vary the lower MF scale and lag values to find a suitable combination.

You can further improve the FLC outputs using a Mamdani type FIS since it also provides lower MF scale and lag parameters for output membership functions. However, a Mamdani type-2 FLC introduces additional computational delay due to the expensive type-reduction process.

References

[1] Mendel, J. M., Uncertain Rule-Based Fuzzy Systems: Introduction and New Directions, Second Edition, Springer, 2017, pp. 229-234, 600-608.

Local Functions

function plotOutput(out,titlePrefix,C,L,T)
figure
plot([0 20],[1 1])
hold on
plot(out.yout{1}.Values)
plot(out.yout{2}.Values)
plot(out.yout{3}.Values)
hold off
grid minor
xlabel("Time (sec)")
ylabel("Output")
title(titlePrefix + ": " + "C=" + C + ", L=" + L + ", T=" + T)
legend(["Reference","PID","Type-1 FLC","Type-2 FLC"], ...
    Location="best")
end

function t = stepResponseTable(out)
s = stepinfo(out.yout{1}.Values.Data,out.yout{1}.Values.Time);
stepResponseInfo(1).RiseTime = s.RiseTime;
stepResponseInfo(1).Overshoot = s.Overshoot;
stepResponseInfo(1).SettlingTime = s.SettlingTime;
stepResponseInfo(1).IAE = out.yout{4}.Values.Data(end);

s = stepinfo(out.yout{2}.Values.Data,out.yout{2}.Values.Time);
stepResponseInfo(2).RiseTime = s.RiseTime;
stepResponseInfo(2).Overshoot = s.Overshoot;
stepResponseInfo(2).SettlingTime = s.SettlingTime;
stepResponseInfo(2).IAE = out.yout{5}.Values.Data(end);

s = stepinfo(out.yout{3}.Values.Data,out.yout{3}.Values.Time);
stepResponseInfo(3).RiseTime = s.RiseTime;
stepResponseInfo(3).Overshoot = s.Overshoot;
stepResponseInfo(3).SettlingTime = s.SettlingTime;
stepResponseInfo(3).IAE = out.yout{6}.Values.Data(end);

t = struct2table(stepResponseInfo, ...
    RowNames=["PID" "Type-1 FLC" "Type-2 FLC"]);
t.Properties.VariableNames(1) = "Rise Time";
t.Properties.VariableNames(2) = t.Properties.VariableNames(2);
t.Properties.VariableNames(3) = "Settling Time";
t.Properties.VariableNames(4) = "Absolute Error";
end

Fuzzy PID Control with Type-2 FIS