使用遗传算法进行多目标优化

简单的多目标优化问题

gamultiobj 可用于解决多变量多目标优化问题。这里我们要最小化两个目标，每个目标都有一个决策变量。

   min F(x) = [objective1(x); objective2(x)]
    x

   where, objective1(x) = (x+2)^2 - 10, and
          objective2(x) = (x-2)^2 + 20

% Plot two objective functions on the same axis
x = -10:0.5:10;
f1 = (x+2).^2 - 10;
f2 = (x-2).^2 + 20;
plot(x,f1);
hold on;
plot(x,f2,'r');
grid on;
title('Plot of objectives ''(x+2)^2 - 10'' and ''(x-2)^2 + 20''');

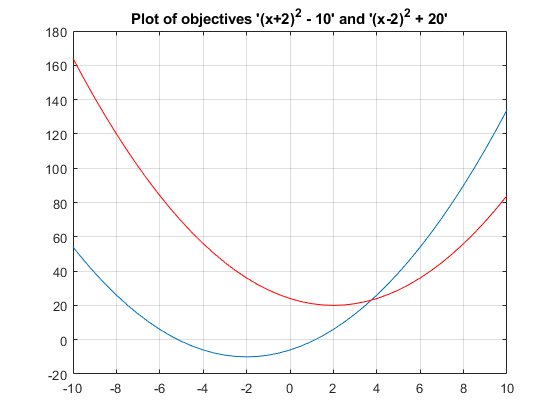
这两个目标的极小值分别在 x = -2 和 x = +2。然而，在多目标问题中，x = -2、x = 2 以及 -2 <= x <= 2 范围内的任何解都同样最优。这个多目标问题没有单一的解。多目标遗传算法的目标是找到该范围内的一组解（理想情况下具有良好的分布）。该组解也称为帕累托前沿。帕累托前沿上的所有解都是最优的。

编写适应度函数

我们创建一个名为 simple_multiobjective.m 的 MATLAB® 文件：

   function y = simple_multiobjective(x)
   y(1) = (x+2)^2 - 10;
   y(2) = (x-2)^2 + 20;

遗传算法求解器假定适应度函数将接受一个输入 x，其中 x 是一个行向量，其元素数量与问题中的变量数量一样多。适应度函数计算每个目标函数的值，并在单个向量输出 y 中返回这些值。

使用 gamultiobj 进行最小化

要使用 gamultiobj 函数，我们需要提供至少两个输入参量、一个适应度函数和问题中的变量数量。gamultiobj 返回的前两个输出参量是 X（帕累托前沿上的点）和 FVAL（X 处的目标函数值）。第三个输出参量 exitFlag 告诉您 gamultiobj 停止的原因。第四个参量 OUTPUT 包含有关求解器性能的信息。gamultiobj 还可以返回第五个参量 POPULATION，其中包含 gamultiobj 终止时的种群，以及第六个参量 SCORE，其中包含 gamultiobj 终止时 POPULATION 的所有目标的函数值。

FitnessFunction = @simple_multiobjective;
numberOfVariables = 1;
[x,fval] = gamultiobj(FitnessFunction,numberOfVariables);

gamultiobj stopped because it exceeded options.MaxGenerations.

求解器返回的 X 是一个矩阵，其中每一行都是目标函数帕累托前沿上的点。FVAL 是一个矩阵，其中每一行包含在 X 中相应点评估的目标函数值。

size(x)
size(fval)

ans =

    18     1


ans =

    18     2

约束多目标优化问题

gamultiobj 可以处理具有线性不等式、等式和简单边界约束的优化问题。这里我们想对之前解决的简单多目标问题添加边界约束。

   min F(x) = [objective1(x); objective2(x)]
    x

   subject to  -1.5 <= x <= 0 (bound constraints)

   where, objective1(x) = (x+2)^2 - 10, and
          objective2(x) = (x-2)^2 + 20

gamultiobj 接受形式为 A*x <= b 的线性不等式约束、形式为 Aeq*x = beq 的线性等式约束和形式为 lb <= x <= ub 的边界约束。我们将 A 和 Aeq 作为矩阵传递，将 b、beq、lb 和 ub 作为向量传递。由于在这个例子中我们没有线性约束，我们将 [] 传递给这些输入。

A = []; b = [];
Aeq = []; beq = [];
lb = -1.5;
ub = 0;
x = gamultiobj(FitnessFunction,numberOfVariables,A,b,Aeq,beq,lb,ub);

gamultiobj stopped because it exceeded options.MaxGenerations.

X（每一行）中的所有解都将满足 options.ConstraintTolerance 中指定的容差范围内的所有线性和边界约束。但是，如果使用自己的交叉或变异函数，请确保新的个体在线性和简单边界约束方面是可行的。

添加可视化

gamultiobj 可以通过选项参量接受一个或多个绘图函数。此功能对于在运行时可视化求解器的性能很有用。可以使用 optimoptions 选择绘图函数。

这里我们使用 optimoptions 来选择两个绘图函数。第一个绘图函数是 gaplotpareto，它绘制每代的帕累托前沿（仅限于任意三个目标）。第二个绘图函数是 gaplotscorediversity，它绘制每个目标的分数多样性。这些选项作为最后一个参量传递给求解器。

options = optimoptions(@gamultiobj,'PlotFcn',{@gaplotpareto,@gaplotscorediversity});
gamultiobj(FitnessFunction,numberOfVariables,[],[],[],[],lb,ub,options);

gamultiobj stopped because it exceeded options.MaxGenerations.

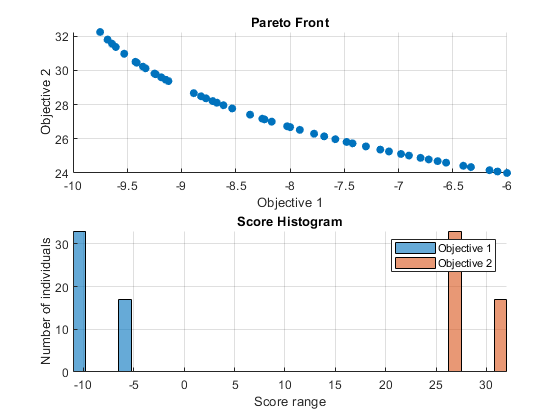
向量化您的适应度函数

再次考虑先前的适应度函数：

   objective1(x) = (x+2)^2 - 10, and
   objective2(x) = (x-2)^2 + 20

默认情况下，gamultiobj 求解器每次仅将一个点传递给适应度函数。然而，如果适应度函数被向量化以接受一组点并返回一组函数值，则可以加快解的速度。

例如，如果求解器需要在一次调用此适应度函数中评估五个点，那么它将使用大小为 5×1 的矩阵调用该函数，即 5 行 1 列（回想一下，1 是变量的数量）。

创建一个名为 vectorized_multiobjective.m 的 MATLAB 文件：

   function scores = vectorized_multiobjective(pop)
     popSize = size(pop,1); % Population size
     numObj = 2;  % Number of objectives
     % initialize scores
     scores = zeros(popSize, numObj);
     % Compute first objective
     scores(:,1) = (pop + 2).^2 - 10;
     % Compute second objective
     scores(:,2) = (pop - 2).^2 + 20;

这个向量化的适应度函数版本采用具有任意数量点的矩阵 pop、pop 的行，并返回大小为 populationSize x numberOfObjectives 的矩阵。

我们需要指定适应度函数使用通过 optimoptions 创建的选项进行向量化。选项作为第九个参量传递。

FitnessFunction = @(x) vectorized_multiobjective(x);
options = optimoptions(@gamultiobj,'UseVectorized',true);
gamultiobj(FitnessFunction,numberOfVariables,[],[],[],[],lb,ub,options);

gamultiobj stopped because the average change in the spread of Pareto solutions is less than options.FunctionTolerance.