焊接梁的设计优化

打开实时脚本

此示例说明如何检查梁的强度和成本之间的权衡。许多出版物都使用此示例作为各种多目标算法的测试问题，包括 Deb 等人 [1] 以及 Ray 和 Liew [2]。

有关此示例的视频概述，请参阅多目标优化的帕累托集。

问题描述

下面的草图改编自 Ray 和 Liew [2]。

该草图代表焊接到基板上的梁。该梁在距基板 L 处支撑负载 P。梁通过上焊缝和下焊缝焊接到基板上，每条焊缝的长度为 l，厚度为 h。该梁的横截面为矩形，宽度为 b，高度为 t。梁的材质是钢。

两个目标是梁的制造成本和施加载荷 P 时梁末端的挠度。载荷 P 固定为 6,000 磅，距离 L 固定为 14 英寸。

设计变量包括：

x(1) = h，焊缝厚度
x(2) = l，焊缝长度
x(3) = t，梁的高度
x(4) = b，光束的宽度

梁的制造成本与梁中的材料量 $(l + L) t b$ 加上焊缝中的材料量 $l h^{2}$ 成正比。使用引用论文中的比例常数，第一个目标是

$F_{1} (x) = 1.10471 x_{1}^{2} x_{2} + 0.04811 x_{3} x_{4} (14 + x_{2}) .$

梁的挠度与 P 成正比，与 $b t^{3}$ 成反比。同样，使用引用论文中的比例常数，第二个目标是

$F_{2} (x) = \frac{P}{x_{4} x_{3}^{3}} C$ ，其中 $C = \frac{4 (14)^{3}}{30 \times 1 0^{6}} \approx 3.6587 \times 1 0^{- 4}$ ， $P = 6, 000$ 。

这个问题有几个约束。

焊缝厚度不能超过梁宽度。用符号表示，x(1) <= x(4)。在工具箱语法中：

Aineq = [1,0,0,-1];
bineq = 0;

焊缝上的剪应力 $τ (x)$ 不能超过 13,600 psi。要计算剪应力，首先计算初步表达式：

$τ_{1} = \frac{1}{\sqrt{2} x_{1} x_{2}}$

$R = \sqrt{x_{2}^{2} + (x_{1} + x_{3})^{2}}$

$τ_{2} = \frac{(L + x_{2} / 2) R}{\sqrt{2} x_{1} x_{3} (x_{2}^{2} / 3 + (x_{1} + x_{3})^{2}}$

$τ (x) = P \sqrt{τ_{1}^{2} + τ_{2}^{2} + \frac{2 τ_{1} τ_{2} x_{2}}{R}} .$

总之，焊缝上的剪应力有约束 $τ (x)$ <= 13600。

焊缝上的法向应力 $σ (x)$ 不能超过 30,000 psi。正常压力是 $P \frac{6 L}{x_{4} x_{3}^{2}} \leq 30 \times 1 0^{3}$ 。
垂直方向的屈曲载荷能力必须超过施加的载荷 6,000 磅。使用杨氏模量 $E = 30 \times 1 0^{6}$ psi 和 $G = 12 \times 1 0^{6}$ psi 的值，屈曲载荷约束为 $\frac{4.013 E x_{3} x_{4}^{3}}{6 L^{2}} (1 - \frac{x_{3}}{2 L} \sqrt{\frac{E}{4 G}}) \geq 6000$ 。从数值上讲，这变成不等式 $64, 746.022 (1 - 0.0282346 x_{3}) x_{3} x_{4}^{3} \geq 6000$ 。
变量的边界为 0.125 <= x(1) <= 5、0.1 <= x(2) <= 10、0.1 <= x(3) <= 10 和 0.125 <= x(4) <= 5。在工具箱语法中：

lb = [0.125,0.1,0.1,0.125];
ub = [5,10,10,5];

目标函数出现在此示例末尾的函数 objval(x) 中。非线性约束出现在此示例末尾的函数 nonlcon(x) 中。

多目标问题公式化和 `paretosearch` 解

您可以通过多种方式优化此问题：

设定最大挠度，并找到满足最大挠度约束的设计的单目标最小制造成本。
设定最大制造成本，并找到满足制造成本约束的设计的单目标最小挠度。
解决多目标问题，可视化两个目标之间的权衡。

要使用多目标方法（它可以提供有关问题的更多信息），请设置目标函数和非线性约束函数。

fun = @objval;
nlcon = @nonlcon;

使用 paretosearch 和 'psplotparetof' 绘图函数解决问题。为了减少诊断显示信息量，请将 Display 选项设置为 'off'。

opts_ps = optimoptions('paretosearch','Display','off','PlotFcn','psplotparetof');
rng default % For reproducibility
[x_ps1,fval_ps1,~,psoutput1] = paretosearch(fun,4,Aineq,bineq,[],[],lb,ub,nlcon,opts_ps);

Figure paretosearch contains an axes object. The axes object with title Pareto Front, xlabel Objective 1, ylabel Objective 2 contains an object of type scatter.

disp("Total Function Count: " + psoutput1.funccount);

Total Function Count: 1467

为了获得更平滑的帕累托前沿，请尝试使用更多点。

npts = 160; % The default is 60
opts_ps.ParetoSetSize = npts;
[x_ps2,fval_ps2,~,psoutput2] = paretosearch(fun,4,Aineq,bineq,[],[],lb,ub,nlcon,opts_ps);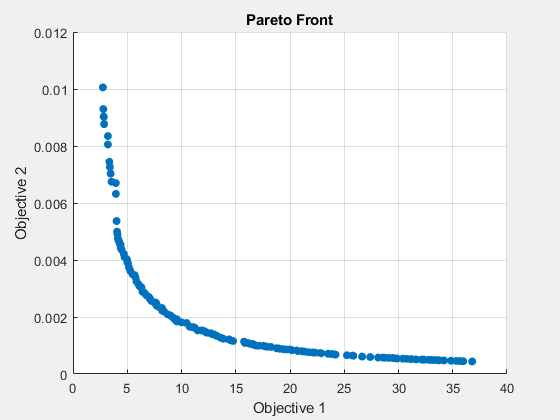

Figure paretosearch contains an axes object. The axes object with title Pareto Front, xlabel Objective 1, ylabel Objective 2 contains an object of type scatter.

disp("Total Function Count: " + psoutput2.funccount);

Total Function Count: 4697

这个解看起来更平滑的曲线。当使用 160 个帕累托点而不是 60 个时，求解器函数计算是原来的三倍多。

`gamultiobj` 解决

要查看求解器是否有所作为，请尝试使用 gamultiobj 求解器解决该问题。设置与上一个解中等效的选项。因为 gamultiobj 求解器在最佳帕累托前沿保留了不到一半的解，所以使用的点数是之前的两倍。

opts_ga = optimoptions('gamultiobj','Display','off','PlotFcn','gaplotpareto','PopulationSize',2*npts);
[x_ga1,fval_ga1,~,gaoutput1] = gamultiobj(fun,4,Aineq,bineq,[],[],lb,ub,nlcon,opts_ga);

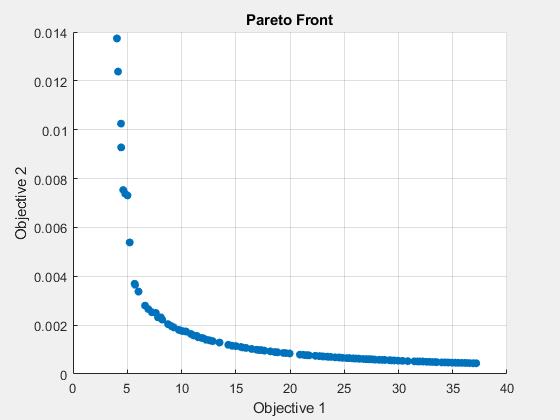
Figure Genetic Algorithm contains an axes object. The axes object with title Pareto Front, xlabel Objective 1, ylabel Objective 2 contains an object of type scatter.

disp("Total Function Count: " + gaoutput1.funccount);

Total Function Count: 33281

gamultiobj 需要数万次函数计算，而 paretosearch 仅需要数千次。gamultiobj 的目标函数值范围稍大一些，尤其是对于目标 2。

对解进行比较

gamultiobj 解似乎与 paretosearch 解不同，尽管由于绘制的比例不同而很难分辨。在同一张图上使用相同的比例绘制两个解。

fps2 = sortrows(fval_ps2,1,'ascend');
figure
hold on
plot(fps2(:,1),fps2(:,2),'r-')
fga = sortrows(fval_ga1,1,'ascend');
plot(fga(:,1),fga(:,2),'b--')
xlim([0,40])
ylim([0,1e-2])
legend('paretosearch','gamultiobj')
xlabel 'Cost'
ylabel 'Deflection'
hold off

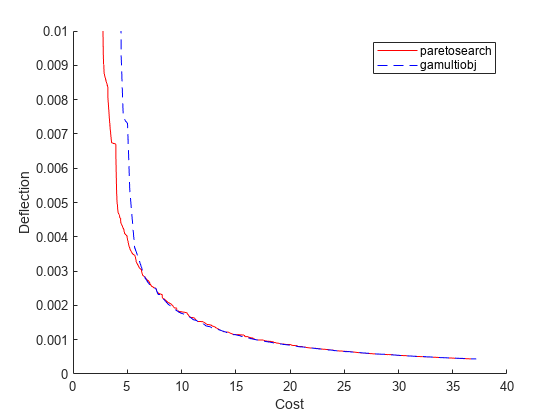
Figure contains an axes object. The axes object with xlabel Cost, ylabel Deflection contains 2 objects of type line. These objects represent paretosearch, gamultiobj.

paretosearch 的解在图的最左侧部分表现更好，其余部分的解看起来难以区分。paretosearch 使用更少的函数计算来获得其解。

通常，当问题没有非线性约束时，paretosearch 至少与 gamultiobj 一样准确。然而，所得到的帕累托集的范围可能会有所不同。

paretosearch 的主要优点之一是它通常需要更少的函数计算。

从单目标解决方案开始

为了帮助求解器找到更好的解，请从最小化个体目标函数的解的点开始。pickindex 函数从 objval 函数返回单个目标。使用 fmincon 来寻找单目标最优。然后使用这些解作为多目标搜索的初始点。

x0 = zeros(2,4);
x0f = (lb + ub)/2;
opts_fmc = optimoptions('fmincon','Display','off','MaxFunctionEvaluations',1e4);
x0(1,:) = fmincon(@(x)pickindex(x,1),x0f,Aineq,bineq,[],[],lb,ub,@nonlcon,opts_fmc);
x0(2,:) = fmincon(@(x)pickindex(x,2),x0f,Aineq,bineq,[],[],lb,ub,@nonlcon,opts_fmc);

检查单目标最优解。

objval(x0(1,:))

ans = 1×2

    2.3810    0.0158

objval(x0(2,:))

ans = 1×2

   76.7188    0.0004

最低成本为 2.381，其挠度为 0.158。最小挠度为 0.0004，成本为 76.7188。绘制的曲线在其范围的末端附近相当陡峭，这意味着如果您采取的成本略高于其最小值，则挠度会少得多，或者如果您采取的挠度略高于其最小值，则成本会少得多。

从单目标解开始 paretosearch。因为您稍后会在同一张图上绘制解，所以请删除 paretosearch 绘图函数。

opts_ps.InitialPoints = x0;
opts_ps.PlotFcn = [];
[x_psx0,fval_ps1x0,~,psoutput1x0] = paretosearch(fun,4,Aineq,bineq,[],[],lb,ub,nlcon,opts_ps);
disp("Total Function Count: " + psoutput1x0.funccount);

Total Function Count: 5007

从相同的初始点开始 ga，并删除其绘图函数。

opts_ga.InitialPopulationMatrix = x0;
opts_ga.PlotFcn = [];
[~,fval_ga,~,gaoutput] = gamultiobj(fun,4,Aineq,bineq,[],[],lb,ub,nlcon,opts_ga);
disp("Total Function Count: " + gaoutput.funccount);

Total Function Count: 33281

在同一轴上绘制解。

fps = sortrows(fval_ps1x0,1,'ascend');
figure
hold on
plot(fps(:,1),fps(:,2),'r-')
fga = sortrows(fval_ga,1,'ascend');
plot(fga(:,1),fga(:,2),'b--')
xlim([0,40])
ylim([0,1e-2])
legend('paretosearch','gamultiobj')
xlabel 'Cost'
ylabel 'Deflection'
hold off

Figure contains an axes object. The axes object with xlabel Cost, ylabel Deflection contains 2 objects of type line. These objects represent paretosearch, gamultiobj.

从单目标解开始，gamultiobj 解在整个绘制范围内与 paretosearch 解相似。然而，gamultiobj 需要几乎十倍的函数计算才能得出其解。

混合函数

gamultiobj 可以自动调用混合函数 fgoalattain 来尝试得出更准确的解。看看混合函数是否能改善解。

opts_ga.HybridFcn = 'fgoalattain';
[xgah,fval_gah,~,gaoutputh] = gamultiobj(fun,4,Aineq,bineq,[],[],lb,ub,nlcon,opts_ga);
disp("Total Function Count: " + gaoutputh.funccount);

Total Function Count: 44923

fgah = sortrows(fval_gah,1,'ascend');
figure
hold on
plot(fps(:,1),fps(:,2),'r-')
plot(fga(:,1),fga(:,2),'b--')
plot(fgah(:,1),fgah(:,2),'g-')
xlim([0,40])
ylim([0,1e-2])
legend('paretosearch','gamultiobj','gamultiobj/fgoalattain')
xlabel 'Cost'
ylabel 'Deflection'
hold off

Figure contains an axes object. The axes object with xlabel Cost, ylabel Deflection contains 3 objects of type line. These objects represent paretosearch, gamultiobj, gamultiobj/fgoalattain.

混合函数对 gamultiobj 解略有改进，主要体现在图的最左侧部分。

从 `paretosearch` 解决方案点手动运行 `fgoalattain`

虽然 paretosearch 没有内置混合函数，但您可以通过从 paretosearch 解点运行 fgoalattain 来改进 paretosearch 解。使用与 gamultiobj 混合函数中描述的 fgoalattain 相同的设置，为 fgoalattain 创建目标和权重。

Fmax = max(fval_ps1x0);
nobj = numel(Fmax);
Fmin = min(fval_ps1x0);
w = sum((Fmax - fval_ps1x0)./(1 + Fmax - Fmin),2);
p = w.*((Fmax - fval_ps1x0)./(1 + Fmax - Fmin));
xnew = zeros(size(x_psx0));
nsol = size(xnew,1);
fvalnew = zeros(nsol,nobj);
opts_fg = optimoptions('fgoalattain','Display','off');
nfv = 0;
for ii = 1:nsol
    [xnew(ii,:),fvalnew(ii,:),~,~,output] = fgoalattain(fun,x_psx0(ii,:),fval_ps1x0(ii,:),p(ii,:),...
        Aineq,bineq,[],[],lb,ub,nlcon,opts_fg);
    nfv = nfv + output.funcCount;
end
disp("fgoalattain Function Count: " + nfv)

fgoalattain Function Count: 10438

fnew = sortrows(fvalnew,1,'ascend');
figure
hold on
plot(fps(:,1),fps(:,2),'r-')
plot(fga(:,1),fga(:,2),'b--')
plot(fgah(:,1),fgah(:,2),'g-')
plot(fnew(:,1),fnew(:,2),'k.-')
xlim([0,40])
ylim([0,1e-2])
legend('paretosearch','gamultiobj','gamultiobj/fgoalattain','paretosearch/fgoalattain')
xlabel 'Cost'
ylabel 'Deflection'

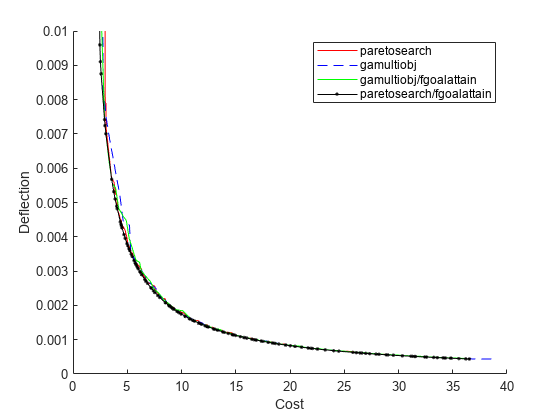
Figure contains an axes object. The axes object with xlabel Cost, ylabel Deflection contains 4 objects of type line. These objects represent paretosearch, gamultiobj, gamultiobj/fgoalattain, paretosearch/fgoalattain.

paretosearch 和 fgoalattain 的组合创建了最准确的帕累托前沿。放大查看。

xlim([3.64 13.69])
ylim([0.00121 0.00442])
hold off

即使有额外的 fgoalattain 计算，组合的总函数数量也还不到单独 gamultiobj 解的函数数量的一半。

fprintf("Total function count for gamultiobj alone is %d.\n" + ...
    "For paretosearch and fgoalattain together it is %d.\n",...
    gaoutput.funccount,nfv + psoutput1x0.funccount)

Total function count for gamultiobj alone is 33281.
For paretosearch and fgoalattain together it is 15445.

从图中找出好的参数

绘制的点显示了函数空间中的最佳值。为了确定哪些参数实现这些函数值，找到梁的尺寸和焊缝的尺寸以获得特定的成本/挠度点。例如，paretosearch 后跟 fgoalattain 的图显示成本约为 6 且挠度约为 3.5e–3 的点。确定达到这些点的梁和焊缝的尺寸。

whichgood = find(fvalnew(:,1) <= 6 & fvalnew(:,2) <= 3.5e-3);
goodpoints = table(xnew(whichgood,:),fvalnew(whichgood,:),'VariableNames',{'Parameters' 'Objectives'})

goodpoints=7×2 table
                   Parameters                       Objectives     
    ________________________________________    ___________________

    0.63052       1.53         10     0.6634    5.6286     0.003309
    0.63907     1.5063         10     0.6829    5.7741    0.0032145
    0.64311     1.4954         10    0.69221    5.8435    0.0031713
    0.61497     1.5749         10     0.6286    5.3681    0.0034922
    0.62035     1.5591         10    0.64056    5.4577     0.003427
    0.63655     1.5132         10    0.67714    5.7311    0.0032419
    0.64834     1.4814         10    0.70433    5.9338    0.0031167

多组参数实现了成本小于 6 且挠度小于 3.5e–3：

焊缝厚度略大于 0.6
焊缝长度约 1.5
梁高 10（上界）
光束宽度在 0.63 和 0.71 之间

目标和非线性约束

function [Cineq,Ceq] = nonlcon(x)
sigma = 5.04e5 ./ (x(:,3).^2 .* x(:,4));
P_c = 64746.022*(1 - 0.028236*x(:,3)).*x(:,3).*x(:,4).^3;
tp = 6e3./sqrt(2)./(x(:,1).*x(:,2));
tpp = 6e3./sqrt(2) .* (14+0.5*x(:,2)).*sqrt(0.25*(x(:,2).^2 + (x(:,1) + x(:,3)).^2)) ./ (x(:,1).*x(:,2).*(x(:,2).^2 / 12 + 0.25*(x(:,1) + x(:,3)).^2));
tau = sqrt(tp.^2 + tpp.^2 + (x(:,2).*tp.*tpp)./sqrt(0.25*(x(:,2).^2 + (x(:,1) + x(:,3)).^2)));
Cineq = [tau - 13600,sigma - 3e4,6e3 - P_c];
Ceq = [];
end

function F = objval(x)
f1 = 1.10471*x(:,1).^2.*x(:,2) + 0.04811*x(:,3).*x(:,4).*(14.0+x(:,2));
f2 = 2.1952./(x(:,3).^3 .* x(:,4));

F = [f1,f2];
end

function z = pickindex(x,k)
    z = objval(x); % evaluate both objectives
    z = z(k); % return objective k
end

参考资料

[1] Deb, Kalyanmoy, J. Sundar, Udaya Bhaskara Rao N, and Shamik Chaudhuri.Reference Point Based Multi-Objective Optimization Using Evolutionary Algorithms.International Journal of Computational Intelligence Research, Vol. 2, No. 3, 2006, pp. 273–286.Available at https://www.softcomputing.net/ijcir/vol2-issu3-paper4.pdf

[2] Ray, T., and K. M. Liew.A Swarm Metaphor for Multiobjective Design Optimization.Engineering Optimization 34, 2002, pp.141–153.