随机目标函数优化
此示例显示如何使用 patternsearch 找到随机目标函数的最小值。它还展示了为什么 Optimization Toolbox™ 求解器不适合解决这类问题。该示例使用一个简单的二维目标函数,然后受到噪声的干扰。
初始化
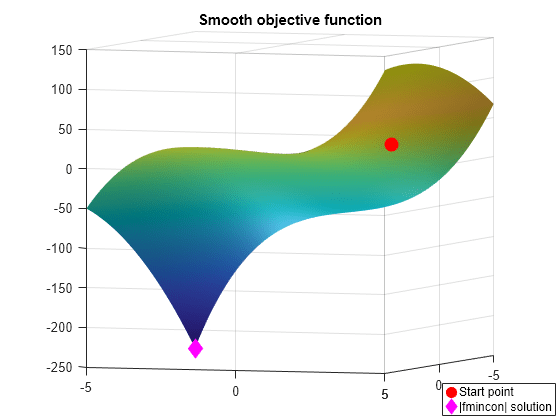
X0 = [2.5 -2.5]; % Starting point. LB = [-5 -5]; % Lower bound UB = [5 5]; % Upper bound range = [LB(1) UB(1); LB(2) UB(2)]; Objfcn = @smoothFcn; % Handle to the objective function. % Plot the smooth objective function fig = figure('Color','w'); showSmoothFcn(Objfcn,range); hold on; title('Smooth objective function'); ph = []; ph(1) = plot3(X0(1),X0(2),Objfcn(X0)+30,'or','MarkerSize',10,'MarkerFaceColor','r'); hold off; ax = gca; ax.CameraPosition = [-31.0391 -85.2792 -281.4265]; ax.CameraTarget = [0 0 -50]; ax.CameraViewAngle = 6.7937; % Add legend information legendLabels = {'Start point'}; lh = legend(ph,legendLabels,'Location','SouthEast'); lp = lh.Position; lh.Position = [1-lp(3)-0.005 0.005 lp(3) lp(4)];

在平滑目标函数上运行 fmincon
目标函数是平滑的(两次连续可微)。使用 Optimization Toolbox fmincon 求解器解决优化问题。fmincon 找到多个变量函数的约束最小值。此函数在点 x* = [-5,-5] 处具有唯一的最小值,该点的值为 f(x*) = -250。
设置选项以返回迭代输出。
options = optimoptions(@fmincon,'Algorithm','interior-point','Display','iter'); [Xop,Fop] = fmincon(Objfcn,X0,[],[],[],[],LB,UB,[],options)
First-order Norm of
Iter F-count f(x) Feasibility optimality step
0 3 -1.062500e+01 0.000e+00 2.004e+01
1 6 -1.578420e+02 0.000e+00 5.478e+01 6.734e+00
2 9 -2.491310e+02 0.000e+00 6.672e+01 1.236e+00
3 12 -2.497554e+02 0.000e+00 2.397e-01 6.310e-03
4 15 -2.499986e+02 0.000e+00 5.065e-02 8.016e-03
5 18 -2.499996e+02 0.000e+00 9.708e-05 3.367e-05
6 21 -2.500000e+02 0.000e+00 1.513e-04 6.867e-06
7 24 -2.500000e+02 0.000e+00 1.161e-06 6.920e-08
Local minimum found that satisfies the constraints.
Optimization completed because the objective function is non-decreasing in
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.
<stopping criteria details>
Xop = 1×2
-5.0000 -5.0000
Fop = -250.0000
figure(fig);
hold on;
绘制最终点
ph(2) = plot3(Xop(1),Xop(2),Fop,'dm','MarkerSize',10,'MarkerFaceColor','m'); % Add a legend to plot legendLabels = [legendLabels, '|fmincon| solution']; lh = legend(ph,legendLabels,'Location','SouthEast'); lp = lh.Position; lh.Position = [1-lp(3)-0.005 0.005 lp(3) lp(4)]; hold off;
随机目标函数
现在通过添加随机噪声来扰乱目标函数。
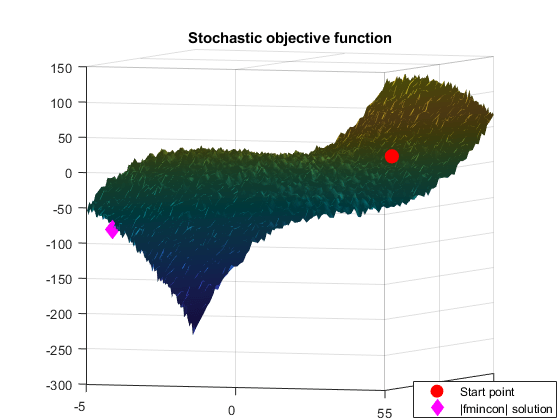
rng(0,'twister') % Reset the global random number generator peaknoise = 4.5; Objfcn = @(x) smoothFcn(x,peaknoise); % Handle to the objective function. % Plot the objective function (non-smooth) fig = figure('Color','w'); showSmoothFcn(Objfcn,range); title('Stochastic objective function') ax = gca; ax.CameraPosition = [-31.0391 -85.2792 -281.4265]; ax.CameraTarget = [0 0 -50]; ax.CameraViewAngle = 6.7937;
在随机目标函数上运行 fmincon
扰动的目标函数是随机的并且不平滑。fmincon 是一个通用的约束优化求解器,它使用目标函数的导数来寻找局部最小值。如果您不提供目标函数的一阶导数,fmincon 将使用有限差分来近似导数。在这个例子中,目标函数是随机的,因此有限差分估计导数可能不可靠。fmincon 可能会停止在非最小点。这可能是因为由于噪音,最佳条件似乎在最终点得到满足,或者 fmincon 无法取得进一步进展。
[Xop,Fop] = fmincon(Objfcn,X0,[],[],[],[],LB,UB,[],options)
First-order Norm of
Iter F-count f(x) Feasibility optimality step
0 3 -1.925772e+01 0.000e+00 2.126e+08
1 6 -7.107849e+01 0.000e+00 2.623e+08 8.873e+00
2 11 -8.055890e+01 0.000e+00 2.401e+08 6.715e-01
3 20 -8.325315e+01 0.000e+00 7.348e+07 3.047e-01
4 48 -8.366302e+01 0.000e+00 1.762e+08 1.593e-07
5 64 -8.591081e+01 0.000e+00 1.569e+08 3.111e-10
Local minimum possible. Constraints satisfied.
fmincon stopped because the size of the current step is less than
the value of the step size tolerance and constraints are
satisfied to within the value of the constraint tolerance.
<stopping criteria details>
Xop = 1×2
-4.9628 2.6673
Fop = -85.9108
figure(fig); hold on; ph = []; ph(1) = plot3(X0(1),X0(2),Objfcn(X0)+30,'or','MarkerSize',10,'MarkerFaceColor','r'); ph(2) = plot3(Xop(1),Xop(2),Fop,'dm','MarkerSize',10,'MarkerFaceColor','m'); % Add legend to plot legendLabels = {'Start point','|fmincon| solution'}; lh = legend(ph,legendLabels,'Location','SouthEast'); lp = lh.Position; lh.Position = [1-lp(3)-0.005 0.005 lp(3) lp(4)]; hold off;
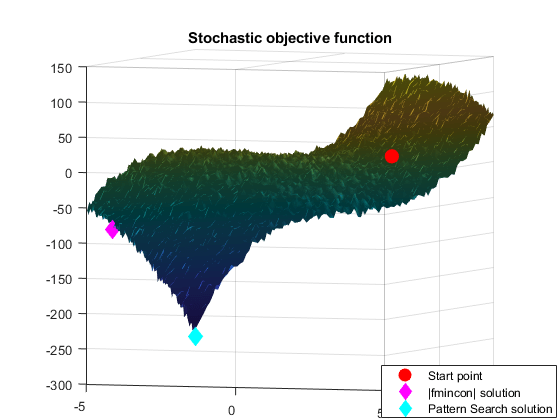
运行 patternsearch
现在使用 Global Optimization Toolbox patternsearch 求解器最小化随机目标函数。模式搜索优化技术是一类直接搜索优化方法。模式搜索算法不使用目标函数的导数来寻找最优点。
PSoptions = optimoptions(@patternsearch,'Display','iter'); [Xps,Fps] = patternsearch(Objfcn,X0,[],[],[],[],LB,UB,PSoptions)
Iter Func-count f(x) MeshSize Method
0 1 -7.20766 1
1 3 -34.7227 2 Successful Poll
2 3 -34.7227 1 Refine Mesh
3 5 -34.7227 0.5 Refine Mesh
4 8 -96.0847 1 Successful Poll
5 10 -96.0847 0.5 Refine Mesh
6 13 -132.888 1 Successful Poll
7 15 -132.888 0.5 Refine Mesh
8 17 -132.888 0.25 Refine Mesh
9 20 -197.689 0.5 Successful Poll
10 22 -197.689 0.25 Refine Mesh
11 24 -197.689 0.125 Refine Mesh
12 27 -241.344 0.25 Successful Poll
13 29 -241.344 0.125 Refine Mesh
14 31 -254.624 0.25 Successful Poll
15 33 -254.624 0.125 Refine Mesh
16 35 -254.624 0.0625 Refine Mesh
17 37 -254.624 0.03125 Refine Mesh
18 39 -254.624 0.01562 Refine Mesh
19 41 -254.624 0.007812 Refine Mesh
20 42 -256.009 0.01562 Successful Poll
21 44 -256.009 0.007812 Refine Mesh
22 47 -256.009 0.003906 Refine Mesh
23 50 -256.009 0.001953 Refine Mesh
24 53 -256.009 0.0009766 Refine Mesh
25 56 -256.009 0.0004883 Refine Mesh
26 59 -256.009 0.0002441 Refine Mesh
27 62 -256.009 0.0001221 Refine Mesh
28 65 -256.009 6.104e-05 Refine Mesh
29 68 -256.009 3.052e-05 Refine Mesh
30 71 -256.009 1.526e-05 Refine Mesh
Iter Func-count f(x) MeshSize Method
31 74 -256.009 7.629e-06 Refine Mesh
32 77 -256.009 3.815e-06 Refine Mesh
33 80 -256.009 1.907e-06 Refine Mesh
34 83 -256.009 9.537e-07 Refine Mesh
patternsearch stopped because the mesh size was less than options.MeshTolerance.
Xps = 1×2
-4.9688 -5.0000
Fps = -256.0095
figure(fig); hold on; ph(3) = plot3(Xps(1),Xps(2),Fps,'dc','MarkerSize',10,'MarkerFaceColor','c'); % Add legend to plot legendLabels = [legendLabels, 'Pattern Search solution']; lh = legend(ph,legendLabels,'Location','SouthEast'); lp = lh.Position; lh.Position = [1-lp(3)-0.005 0.005 lp(3) lp(4)]; hold off
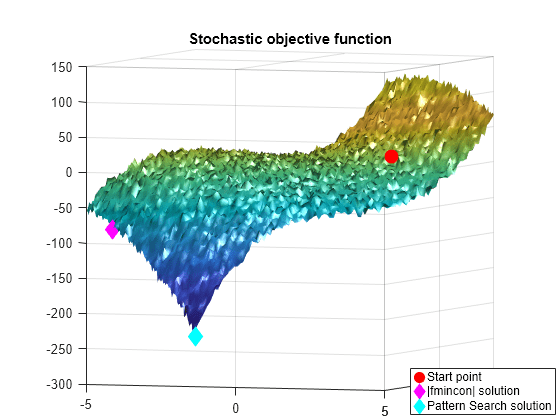
模式搜索不会受到目标函数中随机噪声的强烈影响。模式搜索只需要函数值而不是导数,因此噪声(某种均匀类型)可能不会影响它。然而,与基于导数的算法相比,模式搜索需要更多的函数评估来找到真实最小值,这是不使用导数的代价。
版权所有 2012–2024 The MathWorks, Inc.