调整粒子群优化过程
此示例说明如何使用 particleswarm 求解器进行优化。粒子群算法使种群粒子(称为群)向目标函数的最小值移动。群中每个粒子的速度根据三个因素而变化:
惯性的影响(
InertiaRange选项)对粒子访问过的最佳位置的吸引力(
SelfAdjustmentWeight选项)对邻近粒子中最佳位置的吸引力(
SocialAdjustmentWeight选项)
此示例显示了改变粒子群选项的一些效果。
何时修改选项
通常,particleswarm 使用其默认选项时会找到一个好的解。例如,它使用默认选项很好地优化了 rastriginsfcn。该函数具有许多局部极小值,在点 0 处有一个全局最小值 [0,0]。
rng default % for reproducibility [x,fval,exitflag,output] = particleswarm(@rastriginsfcn,2);
Optimization ended: relative change in the objective value over the last OPTIONS.MaxStallIterations iterations is less than OPTIONS.FunctionTolerance.
formatstring = 'particleswarm reached the value %f using %d function evaluations.\n';
fprintf(formatstring,fval,output.funccount)particleswarm reached the value 0.000000 using 2560 function evaluations.
对于此函数,您知道最佳目标值,因此您知道求解器找到了它。但如果您不知道解该怎么办?评估解质量的一种方法是重新运行求解器。
[x,fval,exitflag,output] = particleswarm(@rastriginsfcn,2);
Optimization ended: relative change in the objective value over the last OPTIONS.MaxStallIterations iterations is less than OPTIONS.FunctionTolerance.
fprintf(formatstring,fval,output.funccount)
particleswarm reached the value 0.000000 using 1480 function evaluations.
解和函数计算的次数都与之前的运行相似。这表明求解器能够顺利地找到解。
使用默认参数的困难目标函数
众所周知,Rosenbrock 函数是一个难以优化的函数。此示例使用了 Rosenbrock 函数的多维版本。该函数在点 0 处具有最小值 [1,1,1,...]。
rng default % for reproducibility nvars = 6; % choose any even value for nvars fun = @multirosenbrock; [x,fval,exitflag,output] = particleswarm(fun,nvars);
Optimization ended: relative change in the objective value over the last OPTIONS.MaxStallIterations iterations is less than OPTIONS.FunctionTolerance.
fprintf(formatstring,fval,output.funccount)
particleswarm reached the value 3106.436648 using 12960 function evaluations.
求解器没有找到很好的解。
限制搜索空间
尝试限制空间以帮助求解器找到一个好点。
lb = -10*ones(1,nvars); ub = -lb; [xbounded,fvalbounded,exitflagbounded,outputbounded] = particleswarm(fun,nvars,lb,ub);
Optimization ended: relative change in the objective value over the last OPTIONS.MaxStallIterations iterations is less than OPTIONS.FunctionTolerance.
fprintf(formatstring,fvalbounded,outputbounded.funccount)
particleswarm reached the value 0.000006 using 71160 function evaluations.
求解器找到了一个更好的解。但要做到这一点需要大量的函数计算。
更改选项
如果求解器更加关注整个空间中的最佳邻居而不是某个较小的邻域,它或许会收敛得更快。
options = optimoptions('particleswarm','MinNeighborsFraction',1); [xn,fvaln,exitflagn,outputn] = particleswarm(fun,nvars,lb,ub,options);
Optimization ended: relative change in the objective value over the last OPTIONS.MaxStallIterations iterations is less than OPTIONS.FunctionTolerance.
fprintf(formatstring,fvaln,outputn.funccount)
particleswarm reached the value 0.000462 using 30180 function evaluations.
虽然求解器采用了较少的函数计算,但尚不清楚这是由于随机性还是由于更好的选项设置。
也许您应该提出 SelfAdjustmentWeight 选项。
options.SelfAdjustmentWeight = 1.9; [xn2,fvaln2,exitflagn2,outputn2] = particleswarm(fun,nvars,lb,ub,options);
Optimization ended: relative change in the objective value over the last OPTIONS.MaxStallIterations iterations is less than OPTIONS.FunctionTolerance.
fprintf(formatstring,fvaln2,outputn2.funccount)
particleswarm reached the value 0.000074 using 18780 function evaluations.
这次 particleswarm 进行的函数计算更少了。这种改进是由于随机性,还是选项设置真的有价值?重新运行求解器并查看函数计算的次数。
[xn3,fvaln3,exitflagn3,outputn3] = particleswarm(fun,nvars,lb,ub,options);
Optimization ended: relative change in the objective value over the last OPTIONS.MaxStallIterations iterations is less than OPTIONS.FunctionTolerance.
fprintf(formatstring,fvaln3,outputn3.funccount)
particleswarm reached the value 0.157026 using 53040 function evaluations.
这次,函数计算的次数增加了。显然,这个 SelfAdjustmentWeight 设置不一定能提高性能。
提供起点
如果 particleswarm 从距离解不太远的已知点开始,也许效果会更好。试试初始点。给出几个个体处于相同的初始点。它们的随机速度确保它们不会保持在一起。
x0 = zeros(20,6); % set 20 individuals as row vectors options.InitialSwarmMatrix = x0; % the rest of the swarm is random [xn3,fvaln3,exitflagn3,outputn3] = particleswarm(fun,nvars,lb,ub,options);
Optimization ended: relative change in the objective value over the last OPTIONS.MaxStallIterations iterations is less than OPTIONS.FunctionTolerance.
fprintf(formatstring,fvaln3,outputn3.funccount)
particleswarm reached the value 0.039015 using 32100 function evaluations.
函数计算的次数再次减少。
向量化以提高速度
multirosenbrock 函数允许向量化函数评估。这意味着它可以同时评估群中所有粒子的目标函数。这通常会大大加快求解器的速度。
rng default % do a fair comparison options.UseVectorized = true; tic [xv,fvalv,exitflagv,outputv] = particleswarm(fun,nvars,lb,ub,options);
Optimization ended: relative change in the objective value over the last OPTIONS.MaxStallIterations iterations is less than OPTIONS.FunctionTolerance.
toc
Elapsed time is 0.414065 seconds.
options.UseVectorized = false;
rng default
tic
[xnv,fvalnv,exitflagnv,outputnv] = particleswarm(fun,nvars,lb,ub,options);Optimization ended: relative change in the objective value over the last OPTIONS.MaxStallIterations iterations is less than OPTIONS.FunctionTolerance.
toc
Elapsed time is 0.470726 seconds.
向量化计算所花的时间大约是串行计算的一半。
绘图函数
您可以使用绘图函数查看求解器的进度。
options = optimoptions(options,'PlotFcn',@pswplotbestf); rng default [x,fval,exitflag,output] = particleswarm(fun,nvars,lb,ub,options);
Optimization ended: relative change in the objective value over the last OPTIONS.MaxStallIterations iterations is less than OPTIONS.FunctionTolerance.

fprintf(formatstring,fval,output.funccount)
particleswarm reached the value 0.079755 using 24960 function evaluations.
使用更多粒子
通常,使用更多的粒子可以获得更准确的解。
rng default
options.SwarmSize = 200;
[x,fval,exitflag,output] = particleswarm(fun,nvars,lb,ub,options);Optimization ended: relative change in the objective value over the last OPTIONS.MaxStallIterations iterations is less than OPTIONS.FunctionTolerance.
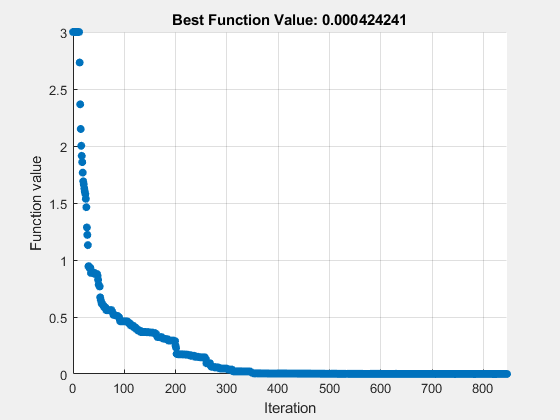
fprintf(formatstring,fval,output.funccount)
particleswarm reached the value 0.000424 using 169400 function evaluations.
混合函数
particleswarm 可以通过搜索多个吸引盆来找到一个好的局部解。但有时它无法达到足够准确的局部最小值。尝试通过指定在粒子群算法停止后运行的混合函数来改进最终答案。将粒子数量重置为其原始值 60,以查看混合函数带来的区别。
rng default
options.HybridFcn = @fmincon;
options.SwarmSize = 60;
[x,fval,exitflag,output] = particleswarm(fun,nvars,lb,ub,options);Optimization ended: relative change in the objective value over the last OPTIONS.MaxStallIterations iterations is less than OPTIONS.FunctionTolerance.

fprintf(formatstring,fval,output.funccount)
particleswarm reached the value 0.000000 using 25191 function evaluations.
disp(output.hybridflag)
1
虽然混合函数改善了结果,但绘图函数显示的最终值与之前相同。这是因为绘图函数仅显示粒子群算法迭代,而不是混合函数计算。混合函数导致最终的函数值非常接近真实最小值 0。output.hybridflag 字段显示 fmincon 以退出标志 1 停止,这表明 x 是一个真正的局部最小值。