Generate Code Using the Command Line Interface

The easiest way to create CUDA^® kernels is to place the coder.gpu.kernelfun pragma into your primary MATLAB^® function. The primary function is also known as the top-level or entry-point function. When the GPU Coder™ encounters kernelfun pragma, it attempts to parallelize all the computation within this function and then maps it to the GPU.

Learning Objectives

In this tutorial, you learn how to:

Prepare your MATLAB code for CUDA code generation by using the kernelfun pragma.
Create and set up a GPU Coder project.
Define function input properties.
Check for code generation readiness and run-time issues.
Specify code generation properties.
Generate CUDA code by using the codegen command.

Tutorial Prerequisites

This tutorial requires the following products:

MATLAB
MATLAB Coder™
GPU Coder
C compiler
NVIDIA^® GPU enabled for CUDA
CUDA Toolkit and driver
Environment variables for the compilers and libraries. For more information, see Environment Variables

Example: The Mandelbrot Set

Description

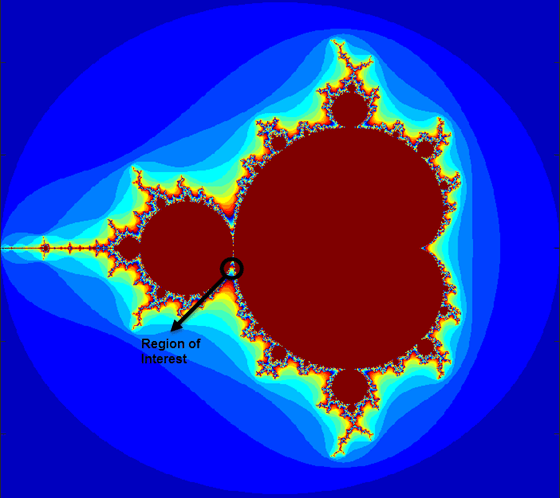
The Mandelbrot set is the region in the complex plane consisting of the values z₀ for which the trajectories defined by this equation remain bounded at k→∞.

$z_{k + 1} = z_{k}^{2} + z_{0}, k = 0, 1, \dots$

The overall geometry of the Mandelbrot set is shown in the figure. This view does not have the resolution to show the richly detailed structure of the fringe just outside the boundary of the set. At increasing magnifications, the Mandelbrot set exhibits an elaborate boundary that reveals progressively finer recursive detail.

Geometry of the Mandelbrot set

Algorithm

For this tutorial, pick a set of limits that specify a highly zoomed part of the Mandelbrot set in the valley between the main cardioid and the p/q bulb to its left. A 1000-by-1000 grid of real parts (x) and imaginary parts (y) is created between these two limits. The Mandelbrot algorithm is then iterated at each grid location. An iteration number of 500 renders the image in full resolution.

maxIterations = 500;
gridSize = 1000;
xlim = [-0.748766713922161,-0.748766707771757];
ylim = [0.123640844894862,0.123640851045266];

This tutorial uses an implementation of the Mandelbrot set by using standard MATLAB commands running on the CPU. This calculation is vectorized such that every location is updated simultaneously.

Tutorial Files

Create a MATLAB script called mandelbrot_count.m with the following lines of code. This code is a baseline vectorized MATLAB implementation of the Mandelbrot set. Later in this tutorial, you modify this file to make it suitable for code generation.

function count = mandelbrot_count(maxIterations, xGrid, yGrid)
% mandelbrot computation

z0 = complex(xGrid,yGrid);
count = ones(size(z0));

z = z0;
for n = 0:maxIterations
    z = z.*z + z0;
    inside = abs(z)<=2;
    count = count + inside;
end
count = log(count);

Create a MATLAB script called mandelbrot_test.m with the following lines of code. The script generates 1000-by-1000 grid of real parts (x) and imaginary parts (y) between the limits specified by xlim and ylim. It also calls the mandelbrot_count function and plots the resulting Mandelbrot set.

maxIterations = 500;
gridSize = 1000;
xlim = [-0.748766713922161, -0.748766707771757];
ylim = [ 0.123640844894862,  0.123640851045266];

x = linspace( xlim(1), xlim(2), gridSize );
y = linspace( ylim(1), ylim(2), gridSize );
[xGrid,yGrid] = meshgrid( x, y );

%% Mandelbrot computation in MATLAB
count = mandelbrot_count(maxIterations, xGrid, yGrid);

% Show
figure(1)
imagesc( x, y, count );
colormap([jet();flipud( jet() );0 0 0]);
axis off
title('Mandelbrot set with MATLAB');

Run the Original MATLAB Code

Run the Mandelbrot Example

Before making the MATLAB version of the Mandelbrot set algorithm suitable for code generation, you can test the functionality of the original code.

Change the current working folder of MATLAB to the location that contains the two files you created in the previous step. GPU Coder places generated code in this folder, change your current working folder if you do not have full access to this folder.
Open the mandelbrot_test script in the MATLAB Editor.
Run the test script by clicking the run button or by entering mandelbrot_test in the MATLAB Command Window.
The test script runs and shows the geometry of the Mandelbrot within the boundary set by the variables xlim and ylim.

Make the MATLAB Code Suitable for Code Generation

To begin the process of making your MATLAB code suitable for code generation, use the file mandelbrot_count.m.

Set your MATLAB current folder to the work folder that contains your files for this tutorial.
In the MATLAB Editor, open mandelbrot_count.m. The file opens in the MATLAB Editor. The Code Analyzer message indicator in the top right corner of the MATLAB Editor is green. The analyzer did not detect errors, warnings, or opportunities for improvement in the code.
Turn on MATLAB for code generation error checking. After the function declaration, add the %#codegen directive.
```
function count = mandelbrot_count(maxIterations, xGrid, yGrid) %#codegen
```
The Code Analyzer message indicator remains green, indicating that it has not detected code generation issues.

To map the mandelbrot_count function to a CUDA kernel, modify the original MATLAB code by placing the coder.gpu.kernelfun pragma outside the for-loop body.

function count = mandelbrot_count(maxIterations, xGrid, yGrid) %#codegen
% mandelbrot computation

z0 = complex(xGrid,yGrid);
count = ones(size(z0));

% Add Kernelfun pragma to trigger kernel creation
coder.gpu.kernelfun;

z = z0;
for n = 0:maxIterations
    z = z.*z + z0;
    inside = abs(z)<=2;
    count = count + inside;
end
count = log(count);

When using the coder.gpu.kernelfun pragma, GPU Coder attempts to map the computations in the function mandelbrot_count to the GPU.

Save the file. You are now ready to compile your code by using the command-line interface.

Code Generation from the Command Line

You can use the codegen command to translate MATLAB functions to a CUDA compatible static or dynamic library, executable, or MEX function, instead of using the GPU Coder app.

Define Input Types

At compile time, GPU Coder must know the data types of all the inputs to the entry-point function. Therefore, if your entry-point function has inputs, you must specify its data type at the time that you compile the file with the codegen function.

You can generate inputs and then use the -args option in the codegen function to let GPU Coder determine the class, size, and complexity of the input parameters. To generate inputs for mandelbrot_count function, use these commands:

maxIterations = 500;
gridSize = 1000;
xlim = [-0.748766713922161, -0.748766707771757];
ylim = [ 0.123640844894862,  0.123640851045266];

x = linspace( xlim(1), xlim(2), gridSize );
y = linspace( ylim(1), ylim(2), gridSize );
[xGrid,yGrid] = meshgrid( x, y );

Alternatively, you can specify the size, type and complexity of the inputs to the entry-point functions without generating input data by using the coder.typeof function.

ARGS = cell(1,1);
ARGS{1} = cell(3,1);
ARGS{1}{1} = coder.typeof(0);
ARGS{1}{2} = coder.typeof(0,[1000 1000]);
ARGS{1}{3} = coder.typeof(0,[1000 1000]);

Build Configuration

To configure build settings such as output file name, location, type, you have to create coder configuration objects. To create the objects, use the coder.gpuConfig function. For example, to create a coder.MexCodeConfig code generation object for use with codegen when generating a MEX function, use:

cfg = coder.gpuConfig('mex');

Other available options are:

cfg = coder.gpuConfig('lib');, to create a code generation configuration object for use with codegen when generating a CUDA static library.
cfg = coder.gpuConfig('dll');, to create a code generation configuration object for use with codegen when generating a CUDA dynamic library.
cfg = coder.gpuConfig('exe');, to create a code generation configuration object for use with codegen when generating a CUDA executable.

For more information, see coder.gpuConfig.

Each configuration object comes with a set of parameters, initialized to default values. You can use dot notation to modify the value of one configuration object parameter at a time. Use this syntax:

configuration_object.property = value

You can enable the same settings as in the Generate Code by Using the GPU Coder App by using the following command-line equivalents:

cfg = coder.gpuConfig('mex');
cfg.GpuConfig.CompilerFlags = '--fmad=false';
cfg.GenerateReport = true;

The cfg configuration object has configuration parameters that are common to MATLAB Coder and GPU Coder and parameters that are GPU Coder-specific. You can see all the GPU-specific properties available in the cfg configuration object by typing cfg.GpuConfig in the MATLAB Command Window.

>> cfg.GpuConfig

ans = 

  GpuCodeConfig with properties:

                    Enabled: 1
                 MallocMode: 'discrete'
           KernelNamePrefix: ''
               EnableCUBLAS: 1
             EnableCUSOLVER: 1
                EnableCUFFT: 1
               Benchmarking: 0
                  SafeBuild: 0
          ComputeCapability: 'Auto'
    CustomComputeCapability: ''
              CompilerFlags: ''
        StackLimitPerThread: 1024
            MallocThreshold: 200
     MaximumBlocksPerKernel: 0
        EnableMemoryManager: 1
           SelectCudaDevice: -1

The --fmad=false flag when passed to the nvcc, instructs the compiler to disable Floating-Point Multiply-Add (FMAD) optimization. This option is set to prevent numerical mismatch in the generated code because of architectural differences in the CPU and the GPU. For more information, see Numerical Differences Between CPU and GPU.

For more information on configuration parameters that are common to MATLAB Coder and GPU Coder, see coder.CodeConfig class.

Build Script

You can create a build script mandelbrot_codegen.m that automates the series of commands mentioned previously.

% GPU code generation for getting started example (mandelbrot_count.m)
%% Create configuration object of class 'coder.MexCodeConfig'.
cfg = coder.gpuConfig('mex');
cfg.GenerateReport = true;
cfg.GpuConfig.CompilerFlags = '--fmad=false';

%% Define argument types for entry-point 'mandelbrot_count'.
ARGS = cell(1,1);
ARGS{1} = cell(3,1);
ARGS{1}{1} = coder.typeof(0);
ARGS{1}{2} = coder.typeof(0,[1000 1000]);
ARGS{1}{3} = coder.typeof(0,[1000 1000]);

%% Invoke GPU Coder.
codegen -config cfg mandelbrot_count -args ARGS{1}

The codegen command opens the file mandelbrot_count.m and translates the MATLAB code into CUDA code.

The -report option instructs codegen to generate a code generation report that you can use to debug your MATLAB code.
The -args option instructs codegen to compile the file mandelbrot_count.m by using the class, size, and complexity of the input parameters maxIterations, xGrid, and yGrid.
The -config option instructs codegen to use the specified configuration object for code generation.

When code generation is successful, you can view the resulting code generation report by clicking View Report in the MATLAB Command Window.

>> mandelbrot_codegen
Code generation successful: View report

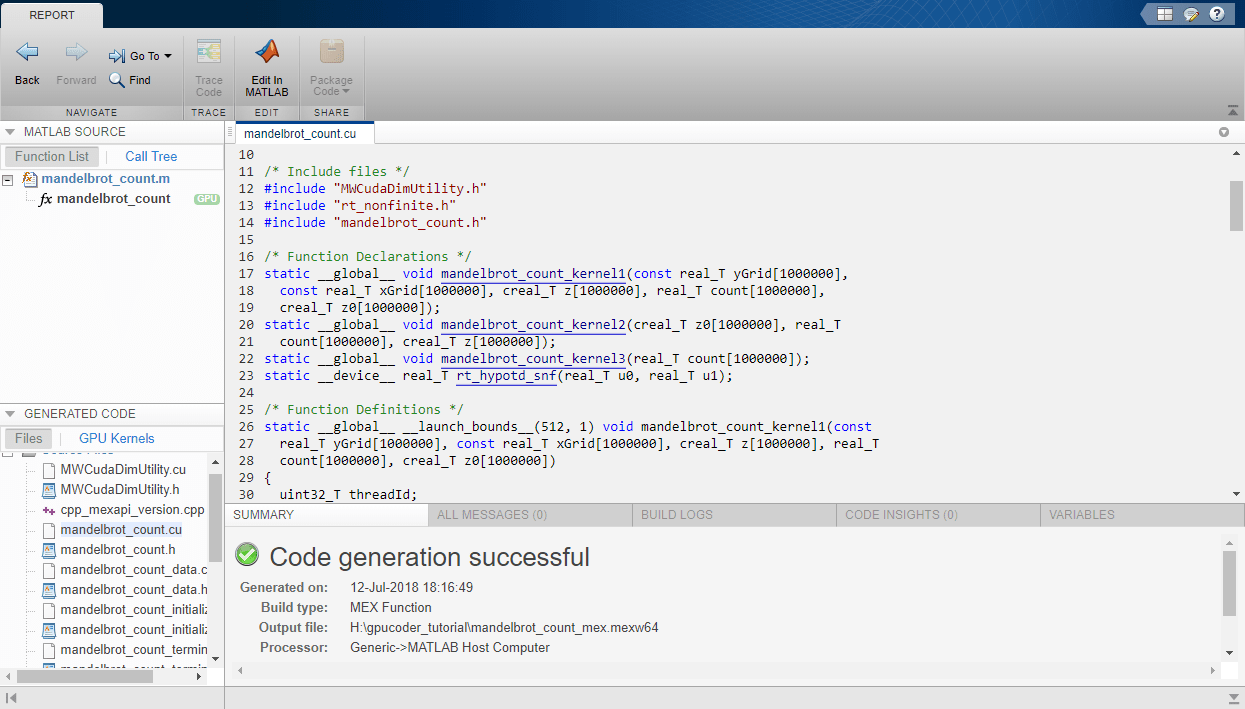
Code generation report window

Verify Correctness of the Generated Code

To verify correctness of the generated MEX file, see Verify Correctness of the Generated Code.