Segmented Pipe LP

(To be removed) Hydraulic pipeline with resistive, fluid inertia, fluid compressibility, and elevation properties

The Hydraulics (Isothermal) library will be removed in a future release. Use the Isothermal Liquid library instead. (since R2020a)

For more information on updating your models, see Upgrading Hydraulic Models to Use Isothermal Liquid Blocks.

Library

Low-Pressure Blocks

Description

The Segmented Pipe LP block models hydraulic pipelines with circular cross sections. Hydraulic pipelines, which are inherently distributed parameter elements, are represented with sets of identical, connected in series, lumped parameter segments. It is assumed that the larger the number of segments, the closer the lumped parameter model becomes to its distributed parameter counterpart. The equivalent circuit of a pipeline adopted in the block is shown below, along with the segment configuration.

Pipeline Equivalent Circuit

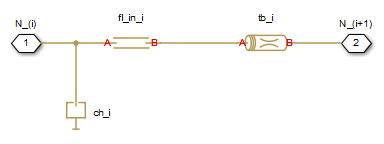
Segment Configuration

The model contains as many Constant Volume Hydraulic Chamber blocks as there are segments. The chamber lumps fluid volume equal to

$V = \frac{π \cdot d^{2}}{4} \frac{L}{N}$

where

`V`	Fluid volume
`d`	Pipe diameter
`L`	Pipe length
`N`	Number of segments

The Constant Volume Hydraulic Chamber block is placed between two branches, each consisting of a Resistive Pipe LP block and a Fluid Inertia block. Every Resistive Pipe LP block lumps (L+L_ad)/(N+1)-th portion of the pipe length, while Fluid Inertia block has L/(N+1) length (L_ad denotes additional pipe length equal to aggregate equivalent length of pipe local resistances, such as fitting, elbows, bends, and so on).

The nodes to which Constant Volume Hydraulic Chamber blocks are connected are assigned names N_1, N_2, …, N_n (n is the number of segments). Pressures at these nodes are assumed to be equal to average pressure of the segment. Intermediate nodes between Resistive Pipe LP and Fluid Inertia blocks are assigned names nn_0, nn_1, nn_2, …, nn_n. The Constant Volume Hydraulic Chamber blocks are named ch_1, ch_2, …, ch_n, Resistive Pipe LP blocks are named tb_0, tb_1, tb_2, …, tb_n, and Fluid Inertia blocks are named fl_in_0, fl_in_1, fl_in_2, …, fl_in_n.

The number of segments determines the number of computational nodes associated with the block. A higher number increases model fidelity but decreases simulation speed. Experiment with different numbers to obtain a suitable trade-off between accuracy and speed. Use the following equation as a starting point in estimating a suitable number of segments:

$N > \frac{4 L}{π \cdot c} ω$

where

`N`	Number of segments
`L`	Pipe length
`c`	Speed of sound in the fluid
ω	Maximum frequency to be observed in the pipe response

The table below contains an example of simulation of a pipeline where the first four true eigenfrequencies are 89.1 Hz, 267 Hz, 446 Hz, and 624 Hz.

Number of Segments	1st Mode	2nd Mode	3rd Mode	4th Mode
1	112.3	–	–	–
2	107.2	271.8	–	–
4	97.7	284.4	432.9	689
8	93.2	271.9	435.5	628

As you can see, the error is less than 5% if an eight-segmented version is used.

The difference in elevation between ports A and B is distributed evenly between pipe segments.

The block positive direction is from port A to port B. This means that the flow rate is positive if it flows from A to B, and the pressure loss is determined as $Δ p = p_{A} - p_{B},$ .

Basic Assumptions and Limitations

Flow is assumed to be fully developed along the pipe length.

Basic Parameters Tab

Pipe internal diameter: Internal diameter of the pipe. The default value is 0.01 m.
Pipe length: Pipe geometrical length. The default value is 5 m.
Number of segments: Number of lumped parameter segments in the pipeline model. The default value is 1.
Aggregate equivalent length of local resistances: This parameter represents total equivalent length of all local resistances associated with the pipe. You can account for the pressure loss caused by local resistances, such as bends, fittings, armature, inlet/outlet losses, and so on, by adding to the pipe geometrical length an aggregate equivalent length of all the local resistances. This length is added to the geometrical pipe length only for hydraulic resistance computation. Both the fluid volume and fluid inertia are determined based on pipe geometrical length only. The default value is 1 m.
Internal surface roughness height: Roughness height on the pipe internal surface. The parameter is typically provided in data sheets or manufacturer’s catalogs. The default value is 1.5e-5 m, which corresponds to drawn tubing.
Laminar flow upper margin: Specifies the Reynolds number at which the laminar flow regime is assumed to start converting into turbulent. Mathematically, this is the maximum Reynolds number at fully developed laminar flow. The default value is 2000.
Turbulent flow lower margin: Specifies the Reynolds number at which the turbulent flow regime is assumed to be fully developed. Mathematically, this is the minimum Reynolds number at turbulent flow. The default value is 4000.
Initial liquid pressure: Gauge pressure in the pipe segments at time zero. Enter a scalar for a single-segment pipeline and a vector for a multi-segment pipeline. The number of elements in the vector must match the number of segments in the pipe. The default value is 0 Pa.

Wall Compliance Tab

Pipe wall type: The parameter can have one of two values: Rigid Wall or Flexible Wall. If the parameter is set to Rigid Wall, wall compliance is not taken into account, which can improve computational efficiency. The value Flexible Wall is recommended for hoses and metal pipes where wall compliance can affect the system behavior. The default value is Rigid Wall.
Static pressure-diameter coefficient: Coefficient that establishes relationship between the pressure and the internal diameter at steady-state conditions. This coefficient can be determined analytically for cylindrical metal pipes or experimentally for hoses. The parameter is used if the Pipe wall type parameter is set to Flexible. The default value is 2e-12 m/Pa.
Viscoelastic process time constant: Time constant in the transfer function that relates pipe internal diameter to pressure variations. By using this parameter, the simulated elastic or viscoelastic process is approximated with the first-order lag. The value is determined experimentally or provided by the manufacturer. The parameter is used if the Pipe wall type parameter is set to Flexible Wall. The default value is 0.01 s.
Specific heat ratio: Gas-specific heat ratio for the Constant Volume Hydraulic Chamber block. The default value is 1.4.

Vertical Position Tab

Port A elevation wrt reference plane: Vertical position of port A with respect to a reference plane. The reference plane is assumed to be the same as that used in the Port B elevation from reference plane parameter. The default value is 0m.
Port B elevation wrt reference plane: Vertical position of port B with respect to a reference plane. The reference plane is assumed to be the same as that used in the Port A elevation from reference plane parameter. The default value is 0m.
Gravitational acceleration: Value of the gravitational acceleration constant (g). The block uses this parameter to compute the effects of an elevation gradient between the ports on their pressure differential. The default value is 9.80655 m/s^2.

Restricted Parameters

When your model is in Restricted editing mode, you cannot modify the following parameter:

Pipe wall type

All other block parameters are available for modification. The actual set of modifiable block parameters depends on the value of the Pipe wall type parameter at the time the model entered Restricted mode.

Global Parameters

Parameters determined by the type of working fluid:

Fluid density
Fluid kinematic viscosity

Use the Hydraulic Fluid block or the Custom Hydraulic Fluid block to specify the fluid properties.

Ports

The block has the following ports:

A: Hydraulic conserving port associated with the pipe inlet.
B: Hydraulic conserving port associated with the pipe outlet.

References

[1] White, F.M., Viscous Fluid Flow, McGraw-Hill, 1991

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2009a

collapse all

R2023a: To be removed

The Hydraulics (Isothermal) library will be removed in a future release. Use the Isothermal Liquid library instead.

For more information on updating your models, see Upgrading Hydraulic Models to Use Isothermal Liquid Blocks.