Perform Parameter Estimation on a Heat Exchanger

If you have a Simulink^® Design Optimization™ license, you can use parameter estimation to parameterize a Simscape™ Fluids™ block without knowing exact details about the heat exchanger geometry. Parameter estimation uses an objective function and a set of initialized parameters to determine the best values to parameterize a given system.

This example shows how to programmatically parameterize an air-water heat exchanger that has an unknown geometry by using test data. To learn how to interactively estimate the parameters, see Parameter Estimator (Simulink Design Optimization).

Load the Model and Associated Data

Open the sscfluids_heat_exchanger_estimation model. This model contains a test harness that uses a Heat Exchanger (G-TL) block to model an air-water heat exchanger. The only available information about the heat exchanger is the general size and the dimensions of the air and water inlets and outlets along with the operational data. To open the model, enter:

exchangerModel = 'sscfluids_heat_exchanger_estimation';
open_system(exchangerModel);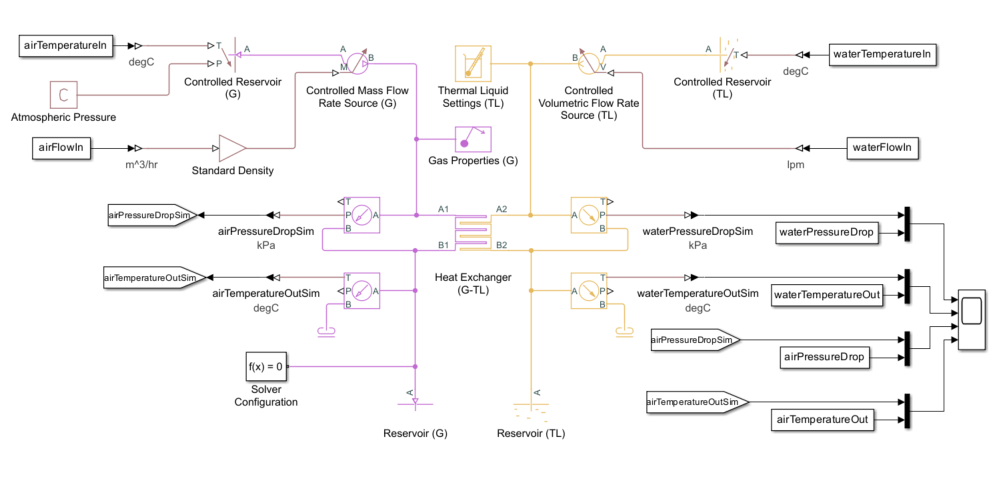

The figure shows the default model.

Heat exchanger estimation test harness model

The gas domain represents the air, and the thermal liquid domain represents the water. The heat exchanger takes inlet temperatures and flow rates of the air and the water as inputs. The heat exchanger outputs are the air and water outlet temperatures and pressure drops. The Scope block compares the outputs with the test data.

Your system test data must represent steady-state measurements from the physical device and can include signal noise. The test data is most effective when it comprises a range of operating conditions. Your goal is to parameterize the heat exchanger such that the outputs match the test data for the given operating conditions within an acceptable tolerance.

load sscfluids_heat_exchanger_estimation_data

This data uses these inputs and outputs:

Inputs	Outputs
`airTemperatureIn`	`airTemperatureOut`
`waterTemperatureIn`	`waterTemperatureOut`
`airFlowIn`	`airPressureDrop`
`waterFlowIn`	`waterPressureDrop`

Each variable is a timeseries object, which requires sample data stored at discrete time intervals.

Design the Parameter Estimation Experiment

To design the parameter estimation experiment:

Create an sdo.Experiment object.
Customize Simulink.SimulationData.Signal objects for each signal to capture the simulation output signals.
Associate the Simulink.SimulationData.Signal objects with the sdo.Experiment object.

Use this code to create the sdo.Experiment object:

exchangerExperiment = sdo.Experiment(exchangerModel);

Create Simulink.SimulationData.Signal objects to store properties and data for each of the four output signals. Set the BlockPath, PortType, PortIndex, Values, and Name properties. Use this code to assign and configure the heat exchanger outputs:

airTemperatureOutSignal = Simulink.SimulationData.Signal;
airTemperatureOutSignal.BlockPath = [exchangerModel '/airTemperatureOutSim'];
airTemperatureOutSignal.PortType = 'outport';
airTemperatureOutSignal.PortIndex = 1;
airTemperatureOutSignal.Values = airTemperatureOut;
airTemperatureOutSignal.Name = get(airTemperatureOut, 'Name');

waterTemperatureOutSignal = Simulink.SimulationData.Signal;
waterTemperatureOutSignal.BlockPath = [exchangerModel '/waterTemperatureOutSim'];
waterTemperatureOutSignal.PortType = 'outport';
waterTemperatureOutSignal.PortIndex = 1;
waterTemperatureOutSignal.Values = waterTemperatureOut;
waterTemperatureOutSignal.Name = get(waterTemperatureOut, 'Name');

airPressureDropSignal = Simulink.SimulationData.Signal;
airPressureDropSignal.BlockPath = [exchangerModel '/airPressureDropSim'];
airPressureDropSignal.PortType = 'outport';
airPressureDropSignal.PortIndex = 1;
airPressureDropSignal.Values = airPressureDrop;
airPressureDropSignal.Name = get(airPressureDrop, 'Name');

waterPressureDropSignal = Simulink.SimulationData.Signal;
waterPressureDropSignal.BlockPath = [exchangerModel '/waterPressureDropSim'];
waterPressureDropSignal.PortType = 'outport';
waterPressureDropSignal.PortIndex = 1;
waterPressureDropSignal.Values = waterPressureDrop;
waterPressureDropSignal.Name = get(waterPressureDrop, 'Name');

Associate the four output signals with the sdo.Experiment object using this code:

exchangerExperiment.OutputData = [
    airTemperatureOutSignal;
    waterTemperatureOutSignal;
    airPressureDropSignal;
    waterPressureDropSignal];

Define the Experimental Parameters

To guide the parameter estimation experiment, define which parameters to estimate and supply initial guesses for the block. Focus on the parameters with the greatest potential performance impact. The most significant heat exchanger parameters are the surface area and the pressure loss coefficient. The surface area affects the rate of heat transfer, which affects the outlet temperature. It encompasses the quantity and size of the tubes and fins. The pressure loss coefficient directly affects the pressure loss at the output. For simplicity, you can fix the other parameters to a single value during the experiment.

Use rough values to parameterize the geometry of the heat exchanger. Because the experiment fits the heat exchanger model to the test data, precise values are unnecessary. To roughly parameterize the heat exchanger model, enter:

airPipeDiameter = 0.35; % m
waterPipeDiameter = 0.025; % m
exchangerLength = 0.6; % m
exchangerDepth = 0.025; % m

These values correspond to the dimensions of the inlet and outlet connections and the general size of the heat exchanger.

Use the sdo.getParameterFromModel function to create a param.Continuous object for each parameter you want to estimate. Include initial, minimum, and maximum values, then associate the data to the experiment. The experiment tunes the parameters to minimize the error between the model output and the test data. Use engineering judgement when selecting the initial guess and boundaries.

airSurfaceAreaInitial = sdo.getParameterFromModel(exchangerModel, 'airSurfaceArea');
airSurfaceAreaInitial.Value = 0.1; % m^2
airSurfaceAreaInitial.Minimum = 0.01;
airSurfaceAreaInitial.Maximum = 10;

waterSurfaceAreaInitial = sdo.getParameterFromModel(exchangerModel, 'waterSurfaceArea');
waterSurfaceAreaInitial.Value = 0.1; % m^2
waterSurfaceAreaInitial.Minimum = 0.01;
waterSurfaceAreaInitial.Maximum = 10;

airLossCoefficientInitial = sdo.getParameterFromModel(exchangerModel, 'airLossCoefficient');
airLossCoefficientInitial.Value = 1;
airLossCoefficientInitial.Minimum = 0.01;
airLossCoefficientInitial.Maximum = 1000;

waterLossCoefficientInitial = sdo.getParameterFromModel(exchangerModel, 'waterLossCoefficient');
waterLossCoefficientInitial.Value = 1;
waterLossCoefficientInitial.Minimum = 0.01;
waterLossCoefficientInitial.Maximum = 1000;

Associate the parameters with the estimation experiment.

exchangerExperiment.Parameters = [
    airSurfaceAreaInitial;
    waterSurfaceAreaInitial;
    airLossCoefficientInitial;
    waterLossCoefficientInitial];

Configure the Initial Simulation

Save time by enabling fast restart mode for the parameters that you want to estimate. This allows Simscape to skip the compilation step after each time Simulink Design Optimization updates a model parameter value. First, open the Heat Exchanger (G-TL) block. Verify that the Pressure loss coefficient and Heat transfer surface area parameters are run-time enabled for both the gas and thermal liquid domains.

Enable fast restart and create an estimation experiment based on an initial simulation.

exchangerSimulator = createSimulator(exchangerExperiment);
exchangerSimulator = fastRestart(exchangerSimulator, 'on');
exchangerSimulator = sim(exchangerSimulator);

Next, collect the results.

logsout = find(exchangerSimulator.LoggedData, get_param(exchangerModel, 'SignalLoggingName'));
airTemperatureOutInitial = find(logsout, 'Air Temperature Out (degC)');
waterTemperatureOutInitial = find(logsout, 'Water Temperature Out (degC)');
airPressureDropInitial = find(logsout, 'Air Pressure Drop (kPa)');
waterPressureDropInitial = find(logsout, 'Water Pressure Drop (kPa)');

Use this code to plot the results against the test data.

figure
tl = tiledlayout(2,2);
nexttile
plot(airTemperatureOut)
hold on
plot(airTemperatureOutInitial.Values)
nexttile
plot(waterTemperatureOut)
hold on
plot(waterTemperatureOutInitial.Values)
nexttile
plot(airPressureDrop)
hold on
plot(airPressureDropInitial.Values)
nexttile
plot(waterPressureDrop)
hold on
plot(waterPressureDropInitial.Values)
set(get(tl, 'Children'), 'Title', [])
legend('Data', 'Initial', Location = 'best')

Observe the significant discrepancy between the simulation results and the test data. These results are acceptable because the simulation outputs are on the same order of magnitude as the heat exchanger data. The parameter estimation experiment iteratively tunes the four experimental parameters until the error between the model output and the test data is smaller than the estimation tolerance. The figure shows the simulation results.

Large discrepancy between initial simulation results and test data

Set Up the Objective Function

To facilitate the experiment, you must set up an objective function that:

Runs the simulation.
Gets the simulation results from signal logging.
Creates a sdo.requirements.SignalTracking object that specifies a tracking requirement for the output signals.
Uses the sdo.requirements.SignalTracking object to compute the error between the model output and the test data.
Returns the error.

The experiment runs the objective function using the current parameters as an argument. As the experiment proceeds, the objective function takes the parameter values of the current iteration and returns the error. The experiment iteratively attempts to reduce the error by adjusting the parameters and running the function to check the updated error measurement, or residual.

Create a function called estimationObjective.m using this code, and add it to your path.

See Code

Perform Parameter Estimation

To begin the parameter estimation experiment, create a function handle that returns the residuals from the estimationObjective.m function and pass that information to the sdo.optimize function.

Create the function handle objFcn to store the residuals using this code:

objFcn = @(p) estimationObjective(p, exchangerSimulator, exchangerExperiment);

Now you can solve the optimization problem. Pass the function handle to sdo.optimize, which evaluates the function at each optimization iteration. Specify the configuration of the optimization experiment using the sdo.OptimizeOptions function.

options = sdo.OptimizeOptions('Method', 'lsqnonlin', 'OptimizedModel', exchangerModel);
parametersEstimated = sdo.optimize(objFcn, exchangerExperiment.Parameters, options);

As Simulink Design Optimization works to achieve a solution, the table results update in the MATLAB^® command window.

  Common Properties:
            Name: 'Air Flow Rate (m^3/hr)'
            Time: [361x1 double]
        TimeInfo: [1x1 tsdata.timemetadata]
            Data: [361x1 double]
        DataInfo: [1x1 tsdata.datametadata]

  More properties, Methods


 Optimization started 24-May-2022 17:01:39

                                          First-order 
 Iter F-count        f(x)      Step-size  optimality
    0      9      501.985            1                                         
    1     18      314.079       0.4605      4.2e+03
    2     27      43.9425        1.942     1.07e+03
    3     36      1.17906        1.096         93.7
    4     45     0.696358       0.1276         21.7
    5     54     0.657429      0.05097         8.13
    6     63     0.649538        0.089         8.99
    7     72     0.646351      0.01974         3.49
    8     81     0.643237     0.003086         3.51
    9     90     0.643237      0.07047         3.51
   10     99     0.643237      0.01762         3.51
   11    108     0.643086     0.004404          5.1
   12    117     0.643086     0.001101          5.1
   13    126     0.643086    0.0002753          5.1
Local minimum possible.
lsqnonlin stopped because the size of the current step is less than
the value of the step size tolerance.

<stopping criteria details>

Display the results in a table.

table(parametersEstimated.Value, 'VariableNames', {parametersEstimated.Name})

ans =

  1×4 table

    airSurfaceArea    waterSurfaceArea    airLossCoefficient    waterLossCoefficient
    ______________    ________________    __________________    ____________________

        1.3311            0.21375               10.002                 100.34

Import the results into the model and run the simulation.

exchangerExperiment = setEstimatedValues(exchangerExperiment, parametersEstimated);
exchangerSimulator = createSimulator(exchangerExperiment, exchangerSimulator);
exchangerSimulator = sim(exchangerSimulator);

Retrieve the estimated simulation results.

logsout = find(exchangerSimulator.LoggedData, get_param(exchangerModel, 'SignalLoggingName'));
airTemperatureOutEstimated = find(logsout, 'Air Temperature Out (degC)');
waterTemperatureOutEstimated = find(logsout, 'Water Temperature Out (degC)');
airPressureDropEstimated = find(logsout, 'Air Pressure Drop (kPa)');
waterPressureDropEstimated = find(logsout, 'Water Pressure Drop (kPa)');

Now you can plot the estimated results against the initial results.

nexttile(tl, 1)
plot(airTemperatureOutEstimated.Values)
nexttile(tl, 2)
plot(waterTemperatureOutEstimated.Values)
nexttile(tl, 3)
plot(airPressureDropEstimated.Values)
nexttile(tl, 4)
plot(waterPressureDropEstimated.Values)
legend('Data', 'Initial', 'Estimated', Location = 'best')

Observe that the estimated results match the test data closely, accounting for noise. The figure shows the plotted results.

Estimated results closely match the test data and are better than the initial guess.