估计 ARIMA 模型

此示例说明如何估计自回归综合移动平均 (ARIMA) 模型。

有时需要包含非平稳趋势（季节性）的时间序列模型。此类模型之一是 ARIMA 模型。这些模型在噪声源中包含一个固定积分器。因此，如果 ARMA 模型的控制方程表示为 A(q)y(t)=Ce(t)，其中 A(q) 表示自回归项，C(q) 表示移动平均项，则 ARIMA 模型的相应模型表示为

$A (q) y (t) = \frac{C (q)}{(1 - q^{- 1})} e (t)$

其中项 $\frac{1}{1 - q^{- 1}}$ 表示离散时间积分器。类似地，您可以为 ARI 和 ARIX 模型制定方程。

使用时间序列模型估计命令 ar、arx 和 armax，您可以将积分器引入噪声源 e(t)。您可以通过使用估计命令中的 IntegrateNoise 参数来执行此操作。

估计方法不考虑时间序列数据中的任何恒定偏移。引入噪声积分器的能力不仅限于时间序列数据。您也可以对输入-输出模型执行此操作，因为其中的干扰可能会受到季节性的影响。一个例子是 ARIMAX 结构的多项式模型：

$A (q) y (t) = B (q) u (t) + \frac{C (q)}{(1 - q^{- 1})} e (t)$

请参阅 armax 参考页面中的示例。

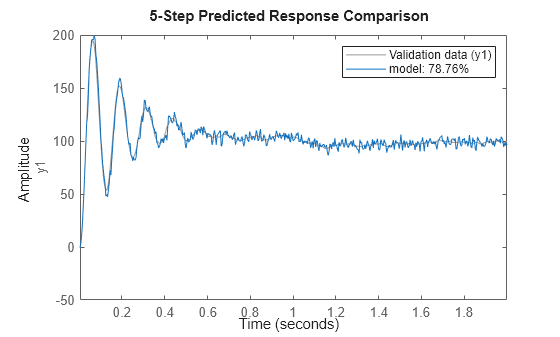
估计具有线性趋势的标量时间序列的 ARI 模型。

load iddata9 z9
Ts = z9.Ts;
y = cumsum(z9.y);
model = ar(y,4,'ls','Ts',Ts,'IntegrateNoise', true);
% 5 step ahead prediction
compare(y,model,5)

Figure contains an axes object. The axes object with ylabel y1 contains 2 objects of type line. These objects represent Validation data (y1), model: 78.76%.

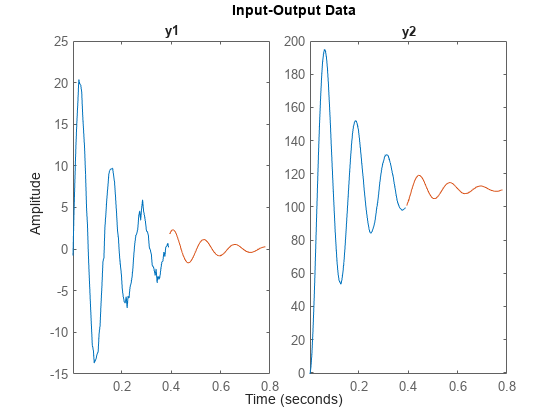
估计一个多元时间序列模型，使得噪声积分仅存在于两个时间序列中的一个中。

load iddata9 z9
Ts = z9.Ts;
y = z9.y;
y2 = cumsum(y);
% artificially construct a bivariate time series
data = iddata([y, y2],[],Ts); na = [4 0; 0 4];
nc = [2;1];
model1 = armax(data, [na nc], 'IntegrateNoise',[false; true]);
% Forecast the time series 100 steps into future
yf = forecast(model1,data(1:100), 100);
plot(data(1:100),yf)

Figure contains 2 axes objects. Axes object 1 with title y1 contains 2 objects of type line. These objects represent untitled1, yf. Axes object 2 with title y2 contains 2 objects of type line. These objects represent untitled1, yf.

如果输出耦合（na 不是对角矩阵），情况会更加复杂，简单地在第二个噪声通道上添加积分器是行不通的。