估计热交换器的传递函数模型

此示例说明如何根据测量信号数据估计传递函数。

热交换器

在这个例子中，我们估计了热交换器的传递函数。热交换器由冷却剂温度、产品温度和干扰环境温度组成。我们将估计冷却剂到产品温度的传递函数。

配置测量数据

测量数据存储在 MATLAB® 文件中，包括冷却液温度围绕标称值的变化测量值和产品温度围绕标称值的变化测量值。

load iddemo_heatexchanger_data

使用 iddata 命令收集测量数据并绘制图表。

data = iddata(pt,ct,Ts);
data.InputName  = '\Delta CTemp';
data.InputUnit  = 'C';
data.OutputName = '\Delta PTemp';
data.OutputUnit = 'C';
data.TimeUnit   = 'minutes';
plot(data)

传递函数估计

从问题的物理原理我们知道热交换器可以用具有延迟的一阶系统来描述。使用 tfest 命令指定一个极点、没有零点以及未知的输入/输出延迟来估计传递函数。

sysTF = tfest(data,1,0,nan)

sysTF =
 
  From input "\Delta CTemp" to output "\Delta PTemp":
                    1.467
  exp(-0.0483*s) * --------
                   s + 1.56
 
Continuous-time identified transfer function.

Parameterization:
   Number of poles: 1   Number of zeros: 0
   Number of free coefficients: 2
   Use "tfdata", "getpvec", "getcov" for parameters and their uncertainties.

Status:                                          
Estimated using TFEST on time domain data "data".
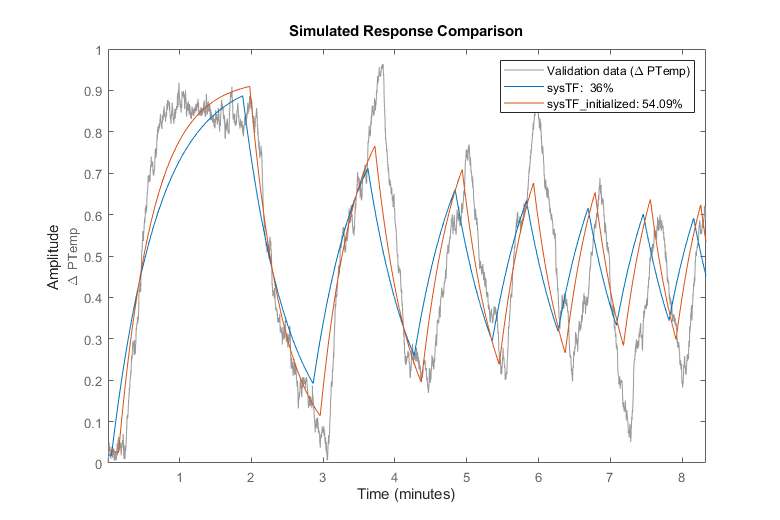
Fit to estimation data: 36%                      
FPE: 0.02625, MSE: 0.02622

compare 和 resid 命令允许我们调查估计模型与测量数据的匹配程度。

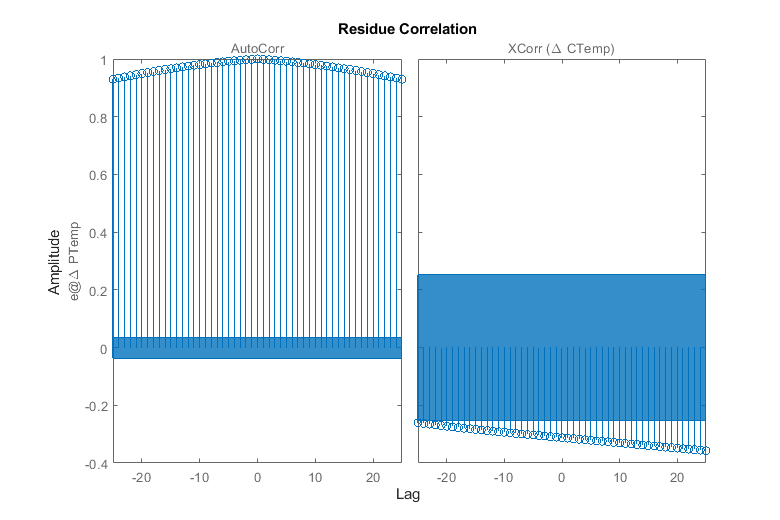
set(gcf,'DefaultAxesTitleFontSizeMultiplier',1,...
   'DefaultAxesTitleFontWeight','normal',...
   'Position',[100 100 780 520]);
resid(sysTF,data);

clf
compare(data,sysTF)

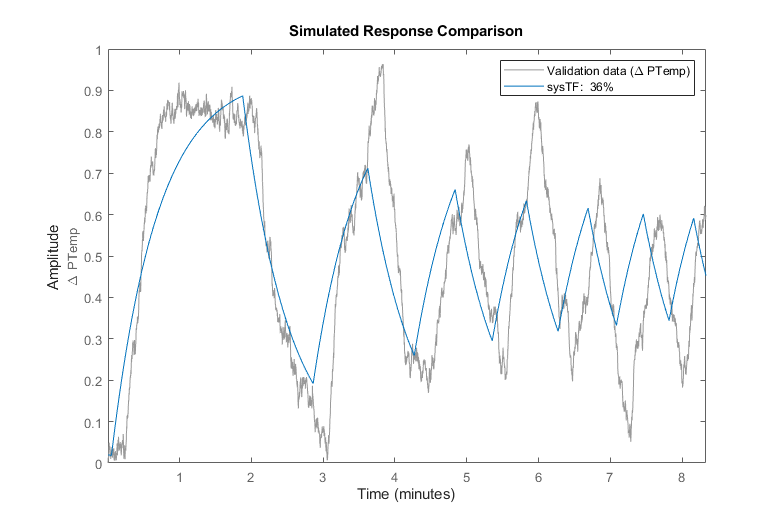
该图显示残差具有很强的相关性，这意味着测量数据中存在一些尚未被估计模型充分捕获的信息。

从初始系统估计传递函数

以前，我们根据数据估计了传递函数，但除了系统顺序之外，并没有包括太多先验知识。从问题的物理原理我们知道系统是稳定的并且具有正增益。检查测量数据我们还知道输入/输出延迟约为 1/5 分钟。我们利用这些信息创建一个初始系统，并利用该系统作为初始猜测来估计传递函数。

sysInit = idtf(NaN,[1 NaN],'ioDelay',NaN);
sysInit.TimeUnit = 'minutes';

限制传递函数的分子和分母项，使得系统稳定且具有正增益。

sysInit.Structure.num.Value   = 1;
sysInit.Structure.num.Minimum = 0;
sysInit.Structure.den.Value   = [1 1];
sysInit.Structure.den.Minimum = [0 0];

将输入/输出延迟限制在 [0 1] 分钟范围内，并使用 1/5 分钟作为初始值。

sysInit.Structure.ioDelay.Value   = 0.2;
sysInit.Structure.ioDelay.Minimum = 0;
sysInit.Structure.ioDelay.Maximum = 1;

使用系统作为估计问题的初始猜测

sysTF_initialized = tfest(data,sysInit)

sysTF_initialized =
 
  From input "\Delta CTemp" to output "\Delta PTemp":
                    1.964
  exp(-0.147*s) * ---------
                  s + 2.115
 
Continuous-time identified transfer function.

Parameterization:
   Number of poles: 1   Number of zeros: 0
   Number of free coefficients: 2
   Use "tfdata", "getpvec", "getcov" for parameters and their uncertainties.

Status:                                          
Estimated using TFEST on time domain data "data".
Fit to estimation data: 54.09%                   
FPE: 0.01351, MSE: 0.01349

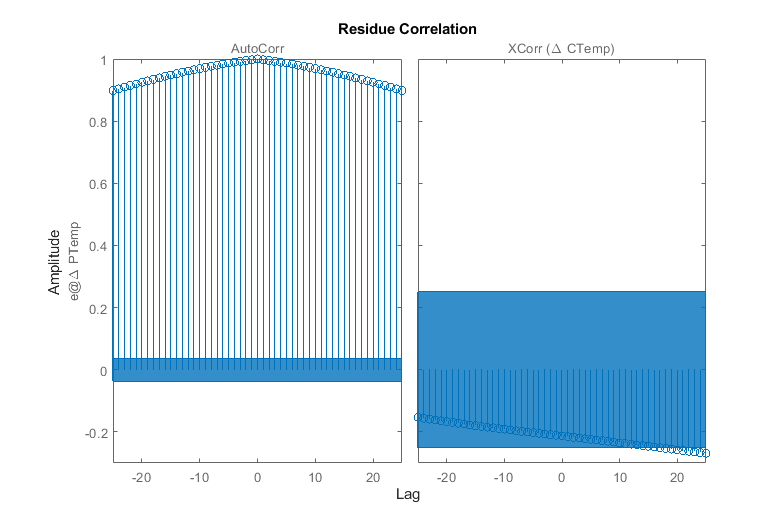
resid(sysTF_initialized,data);

clf
compare(data,sysTF,sysTF_initialized)

过程模型估计

在上面，我们将估计问题视为传递函数估计问题，但我们知道可以施加一些额外的结构。具体来说，热交换器系统是一个具有延迟的一阶过程，或形式为“P1D”模型：

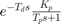
$e^{-T_d s}\frac{K_p}{T_p s+1}$

使用 procest 命令进一步将此结构强加于问题。

sysP1D  = procest(data,'P1D')

sysP1D =
 
Process model with transfer function:
             Kp                      
  G(s) = ---------- * exp(-Td*s)     
          1+Tp1*s                    
                                     
        Kp = 0.90548                 
       Tp1 = 0.32153                 
        Td = 0.25435                 
                                     
Parameterization:
    {'P1D'}
   Number of free coefficients: 3
   Use "getpvec", "getcov" for parameters and their uncertainties.

Status:                                            
Estimated using PROCEST on time domain data "data".
Fit to estimation data: 70.4%                      
FPE: 0.005614, MSE: 0.005607

resid(sysP1D,data);

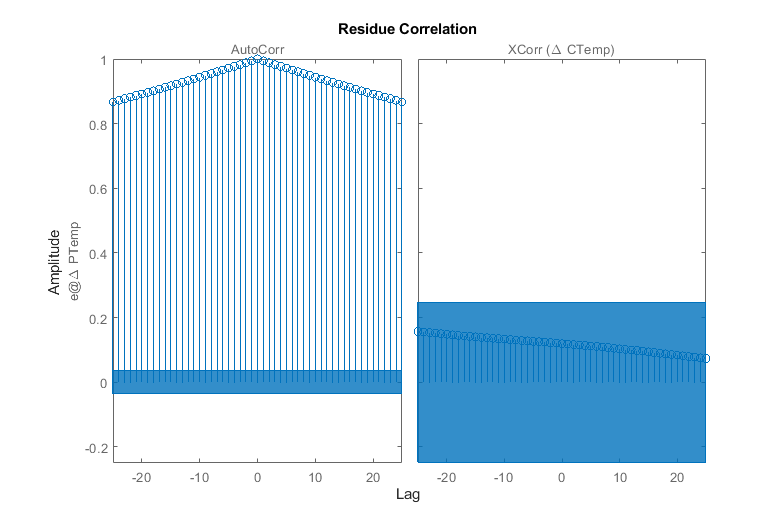
clf
compare(data,sysTF,sysTF_initialized,sysP1D)

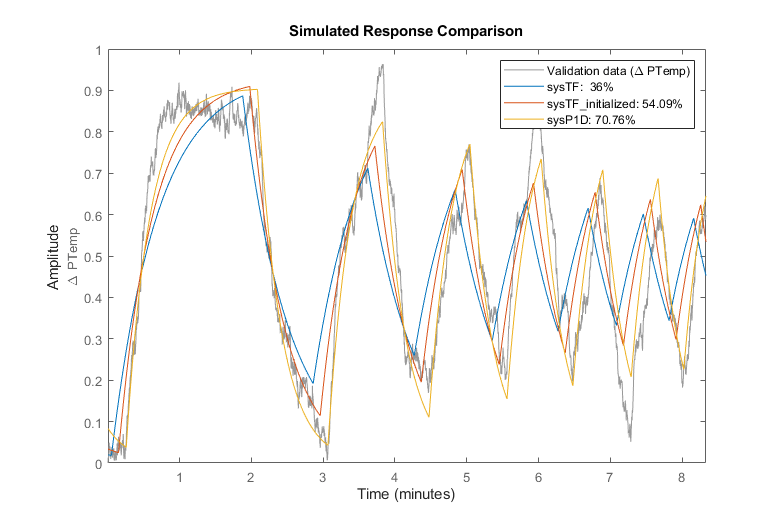
带有扰动模型的过程模型估计

到目前为止执行的所有估计的残差图表明残差相关性仍然很高，这意味着该模型不够丰富，无法解释测量数据中的所有信息。关键缺失部分是干扰环境温度，我们尚未将其纳入模型中。

创建一个对延迟和时间常值有限制的“P1D”过程模型，并将其用作估计问题的初始猜测。

sysInit = idproc('P1D','TimeUnit','minutes');

限制模型具有正增益，并且延迟在 [0 1] 分钟范围内。

sysInit.Structure.Kp.Value    = 1;
sysInit.Structure.Kp.Minimum  = 0;
sysInit.Structure.Tp1.Value   = 1;
sysInit.Structure.Tp1.Maximum = 10;
sysInit.Structure.Td.Value    = 0.2;
sysInit.Structure.Td.Minimum  = 0;
sysInit.Structure.Td.Maximum  = 1;

指定使用一阶模型（“ARMA1”）作为扰动分量的选项。使用模板模型 sysInit 以及选项集来估计模型。

opt = procestOptions('DisturbanceModel','ARMA1');
sysP1D_noise = procest(data,sysInit,opt)

sysP1D_noise =
 
Process model with transfer function:                
             Kp                                      
  G(s) = ---------- * exp(-Td*s)                     
          1+Tp1*s                                    
                                                     
        Kp = 0.91001                                 
       Tp1 = 0.3356                                  
        Td = 0.24833                                 
                                                     
An additive ARMA disturbance model has been estimated
      y = G u + (C/D)e                               
                                                     
      C(s) = s + 591.6                               
      D(s) = s + 3.217                               
                                                     
Parameterization:
    {'P1D'}
   Number of free coefficients: 5
   Use "getpvec", "getcov" for parameters and their uncertainties.

Status:                                            
Estimated using PROCEST on time domain data "data".
Fit to estimation data: 96.86% (prediction focus)  
FPE: 6.307e-05, MSE: 6.294e-05

resid(sysP1D_noise,data);

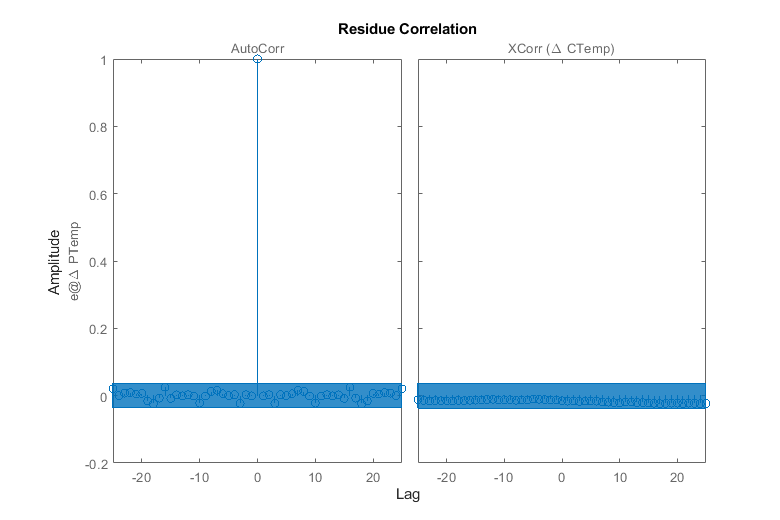
clf
compare(data,sysTF,sysTF_initialized,sysP1D,sysP1D_noise)

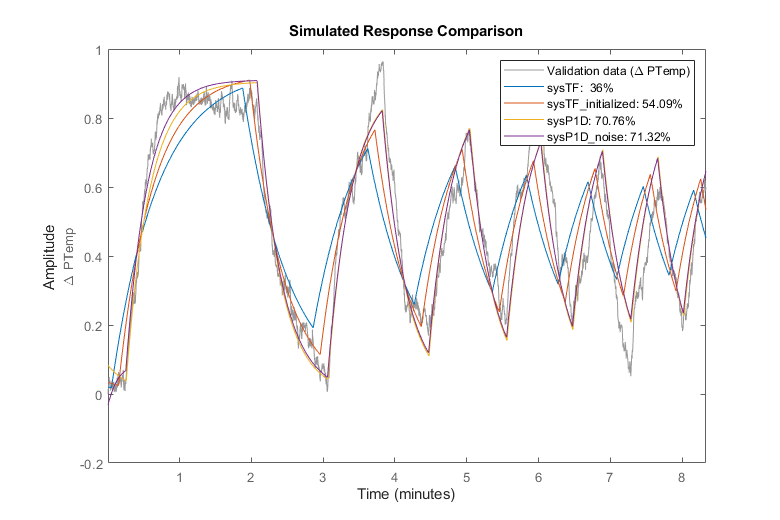
残差图清楚地表明残差是不相关的，这意味着我们有一个可以解释测量数据的模型。我们估计的“ARMA1”扰动分量作为分子和分母值存储在模型的“NoiseTF”属性中。

sysP1D_noise.NoiseTF

ans = 

  struct with fields:

    num: {[1 591.6038]}
    den: {[1 3.2172]}

比较不同模型

虽然我们已经确定了一个可以解释测量数据的模型，但我们注意到该模型与测量数据的拟合度约为 70%。拟合值的损失是环境温度干扰的强烈影响的结果，如下所示。

测量数据是从具有以下精确值的 Simulink 模型获得的（d 是高斯噪声干扰）

   y = (1-pi/100)*exp(-15s)/(21.3s+1)*u + 1/(25s+1)*d

使用这些值创建一个“P1D”模型，并查看该模型与测量数据的拟合程度。

sysReal = idproc('P1D','TimeUnit','minutes');
sysReal.Kp  = 1-pi/100;
sysReal.Td  = 15/60;
sysReal.Tp1 = 21.3/60;
sysReal.NoiseTF = struct('num',{[1 10000]},'den',{[1 0.04]});

compare(data,sysReal,sysTF,sysTF_initialized,sysP1D,sysP1D_noise);

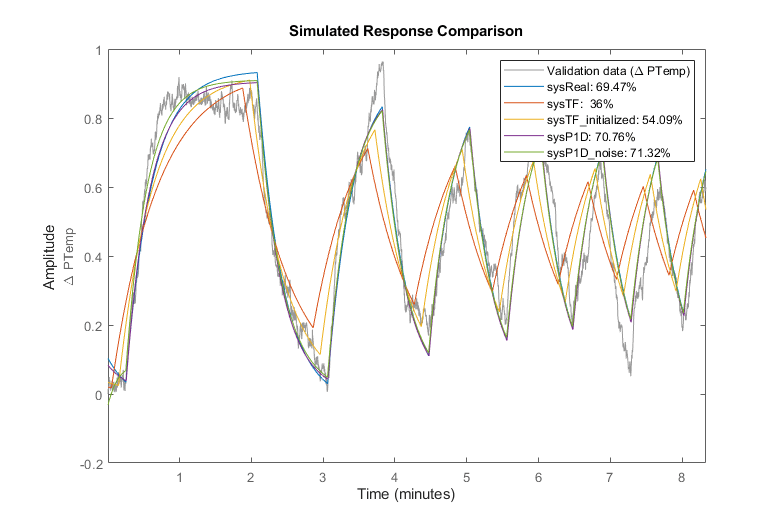
比较图显示，真实系统与测量数据的拟合度也在 70% 左右，证实了我们的估计模型在拟合测量数据方面并不比真实模型差 - 这是环境温度扰动强烈影响的结果。