弹性机翼飞机的模态分析
此示例展示了柔性机翼飞机弯曲模式的计算。机翼的振动响应是在机翼跨度上的多个点收集的。该数据用于辨识系统的动态模型。从辨识模型中提取模态参数。模态参数数据与传感器位置信息相结合,可以直观地看到机翼的各种弯曲模式。此示例需要 Signal Processing Toolbox™。
柔性翼飞机
在这个例子中,我们研究了明尼苏达大学无人驾驶飞行器实验室建造的一架小型柔性飞翼飞机收集的数据 [1]。飞机的几何形状如下所示。
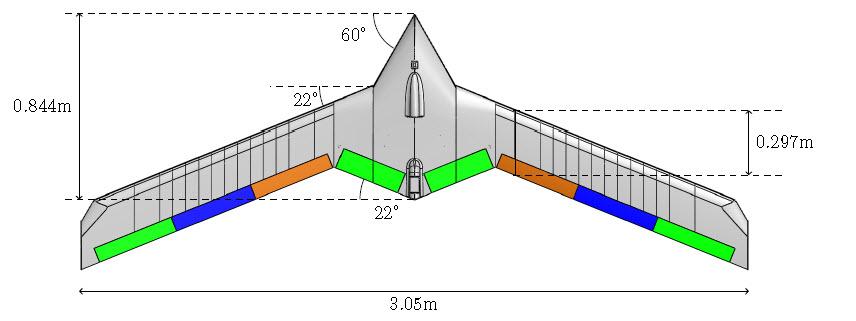
飞机机翼在载荷作用下会发生较大的变形。柔性模式频率比机翼刚性更大的普通飞机的柔性模式频率要低。这种灵活的设计降低了材料成本,提高了飞机的灵活性和飞行距离。然而,如果不加以控制,柔性模式可能会导致灾难性的气动弹性不稳定性(颤振)。设计有效的控制律来抑制这些不稳定性需要准确确定机翼的各种弯曲模式。
试验设置
试验的目标是收集飞机在各个位置对外部激励的振动响应。飞机悬挂在木制框架上,重心处有一个弹簧。弹簧具有足够的柔韧性,使得弹簧质量振动的固有频率不会干扰飞机的基本频率。输入力通过位于飞机中心附近的 Unholtz-Dickie Model 20 电动振动器施加。


沿翼展放置二十个 PCB-353B16 加速度计来收集振动响应,如下图所示。
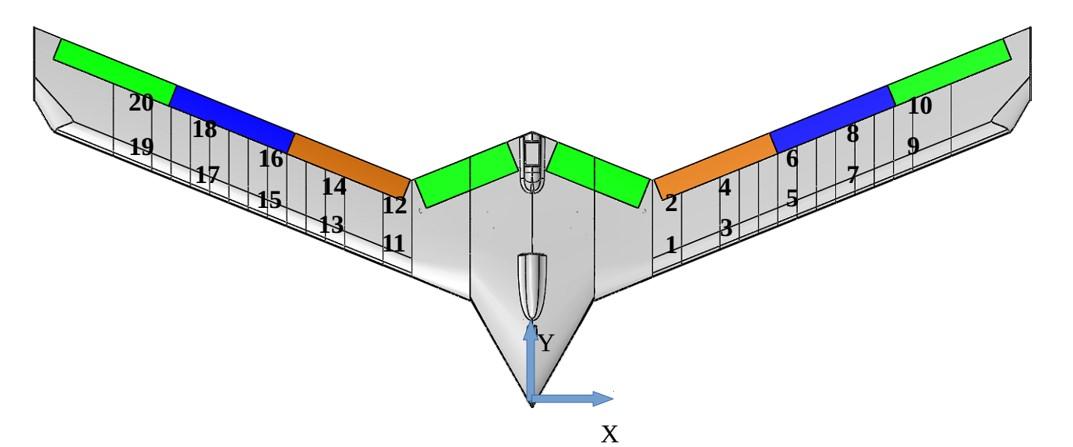
振动器输入命令被指定为形式为 的恒定幅度线性调频输入。啁啾频率随时间线性变化,即 。输入信号覆盖的频率范围是 3–35 Hz。数据由两个加速度计(位于一个 x 位置的前缘加速度计和后缘加速度计)同时收集。因此进行了 10 次试验来收集所有 20 个加速度计响应。加速度计和力传感器测量均以 2000 Hz 的频率进行采样。
数据准备
数据由 10 组双输出/单输入信号表示,每组包含 600K 个采样。该数据可在 MathWorks 支持文件站点上找到。请参阅免责声明。下载数据文件并将数据加载到 MATLAB® 工作区。
url = 'https://www.mathworks.com/supportfiles/ident/flexible-wing-GVT-data/FlexibleWingData.mat'; websave('FlexibleWingData.mat',url); load FlexibleWingData.mat MeasuredData
变量 MeasuredData 是一个包含字段 Exp1、Exp2、...、Exp10 的结构。每个字段都是一个结构,其中字段 y 和 u 包含两个响应和相应的输入力数据。绘制第一个试验的数据。
fs = 2000; % data sampling frequency Ts = 1/fs; % sample time y = MeasuredData.Exp1.y; % output data (2 columns, one for each accelerometer) u = MeasuredData.Exp1.u; % input force data t = (0:length(u)-1)' * Ts; figure subplot(211) plot(t,y) ylabel('Outputs (m/s^2)') legend('Leading edge','Trailing edge') subplot(212) plot(t,u) ylabel('Input') xlabel('Time (seconds)')

为了给模型辨识准备数据,数据被打包成 iddata 对象。iddata 对象是 System Identification Toolbox™ 中打包时域数据的标准方式。输入信号被视为带限信号。
ExpNames = fieldnames(MeasuredData); Data = cell(1, 10); for k = 1:10 y = MeasuredData.(ExpNames{k}).y; u = MeasuredData.(ExpNames{k}).u; Data{k} = iddata(y, u, Ts, 'InterSample', 'bl'); end
将数据集对象合并为一个多试验数据对象。
Data = merge(Data{:})Data =
Time domain data set containing 10 experiments.
Experiment Samples Sample Time
Exp1 600001 0.0005
Exp2 600001 0.0005
Exp3 600001 0.0005
Exp4 600001 0.0005
Exp5 600001 0.0005
Exp6 600001 0.0005
Exp7 600001 0.0005
Exp8 600001 0.0005
Exp9 600001 0.0005
Exp10 600001 0.0005
Outputs Unit (if specified)
y1
y2
Inputs Unit (if specified)
u1
模型辨识
我们希望找到一个频率响应与实际飞机频率响应尽可能接近的动态模型。动态模型将系统输入和输出之间的数学关系封装为微分方程或差分方程。动态模型的例子有传递函数和状态空间模型。在 System Identification Toolbox 中,动态模型被封装为诸如 idtf(用于传递函数)、idpoly(用于 AR、ARMA 模型)和 idss(用于状态空间模型)等对象。可以通过在时域或频域中对测量数据运行估计命令(例如 tfest 和 ssest 命令)来创建动态模型。
对于这个例子,我们首先使用 etfe 命令通过经验传递函数估计将测量的时域数据转换为频率响应数据。然后使用估计的 FRF 来辨识飞机振动响应的状态空间模型。可以直接利用时域数据进行动态模型辨识。然而,FRF 形式的数据允许将大型数据集压缩为更少的采样,并更容易地将估计行为调整到相关的频率范围。FRF 由 idfrd 对象封装。
为每个数据试验估计一个双输出/单输入频率响应函数 (FRF)。不使用加窗。使用 24,000 个频率点进行响应计算。
G = cell(1, 10); N = 24000; for k = 1:10 % Convert time-domain data into a FRF using ETFE command Data_k = getexp(Data, k); G{k} = etfe(Data_k, [], N); % G{k} is an @idfrd object end
将所有 FRF 串联成一个 20 输出/1 输入的 FRF。
G = cat(1, G{:}); % concatenate outputs of all estimated FRFs
G.OutputName = 'y'; % name outputs 'y1', 'y2', ..., 'y20'
G.InterSample = 'bl';为了了解估计的频率响应,绘制输出 1 和 15(任意选择)的幅度。放大感兴趣的频率范围 (4–35 Hz)。
opt = bodeoptions; % plot options opt.FreqUnits = 'Hz'; % show frequency in Hz opt.PhaseVisible = 'off'; % do not show phase OutputNum = [1 15]; % pick outputs 1 and 15 for plotting clf bodeplot(G(OutputNum, :), opt) % plot frequency response xlim([4 35]) grid on
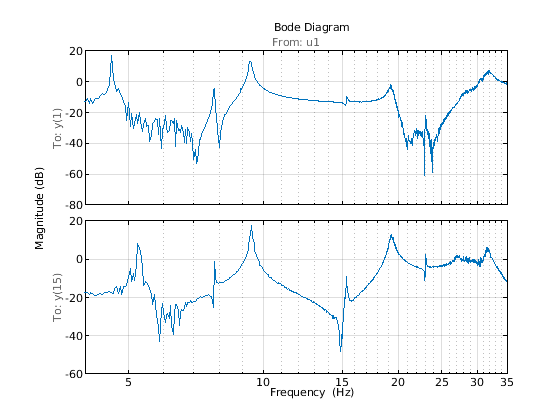
FRF 显示至少 9 个共振频率。为了进行分析,我们希望重点关注 6-35 Hz 频率跨度,这是飞机最关键的柔性弯曲模式所在。因此将 FRF 降低到该频率区域。
f = G.Frequency/2/pi; % extract frequency vector in Hz (G stores frequency in rad/s) Gs = fselect(G, f>6 & f<=32) % "fselect" selects the FRF in the requested range (6.5 - 35 Hz)
Gs = IDFRD model. Contains Frequency Response Data for 20 output(s) and 1 input(s). Response data is available at 624 frequency points, ranging from 37.96 rad/s to 201.1 rad/s. Sample time: 0.0005 seconds Output channels: 'y(1)', 'y(2)', 'y(3)', 'y(4)', 'y(5)', 'y(6)', 'y(7)', 'y(8)', 'y(9)', 'y(10)', 'y(11)', 'y(12)', 'y(13)', 'y(14)', 'y(15)', 'y(16)', 'y(17)', 'y(18)', 'y(19)', 'y(20)' Input channels: 'u1' Status: Estimated model
因此,Gs 包含 20 个测量位置的频率响应测量值。接下来,确定一个状态空间模型来拟合 Gs。子空间估计器 n4sid 提供了快速的非迭代估计。状态空间模型结构配置如下:
我们估计一个 24 阶连续时间模型。在对各种阶数进行一些试验并检查模型与 FRF 的拟合情况后,找到了该阶数。
该模型包含一个馈通通项(D 矩阵非零)。这是因为我们将分析限制在 35 Hz,而机翼的带宽明显大于此(响应在 35 Hz 时显著)。
为了加快计算速度,我们抑制参数协方差的计算。
FRF 幅值在整个频率范围内变化很大。为了确保低振幅与高振幅受到同等重视,我们应用了与响应的平方根成反比的自定义权重。由于有 20 个通道,因此加权向量取从每个通道获得的权重的平均值(这是因为 20 个通道的 FRF 形状相似)。
我们使用 n4sidOptions 为 n4sid 设置了估计选项。
FRF = squeeze(Gs.ResponseData); Weighting = mean(1./sqrt(abs(FRF))).'; n4Opt = n4sidOptions('EstimateCovariance',false,... 'WeightingFilter',Weighting,... 'OutputWeight',eye(20)); sys1 = n4sid(Gs,24,'Ts',0,'Feedthrough',true,n4Opt); Fit = sys1.Report.Fit.FitPercent'
Fit = 1×20
54.2689 55.3738 84.0188 85.7017 81.9259 80.2293 55.7448 40.6773 58.6429 76.2997 83.5370 84.6555 85.9240 84.8780 76.8937 81.0399 74.8321 79.4069 65.0803 76.3328
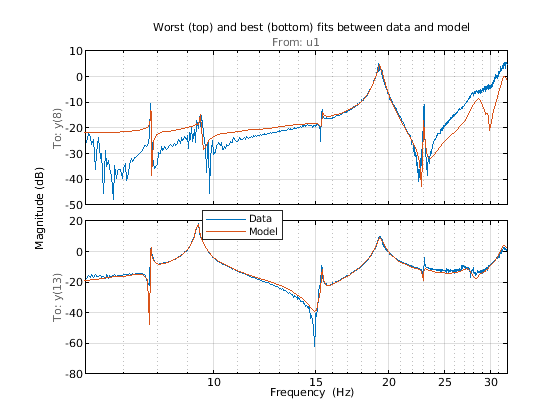
“拟合度”数字使用归一化均方根误差 (NRMSE) 拟合优度测量显示数据 (Gs) 和模型 (sys1) 频率响应之间的百分比拟合度。接下来绘制最差和最佳拟合情况。
[~,Imin] = min(Fit); [~,Imax] = max(Fit); clf bodeplot(Gs([Imin, Imax],:), sys1([Imin, Imax],:), opt); xlim([6 32]) title('Worst (top) and best (bottom) fits between data and model') grid on legend('Data', 'Model')
通过模型参数的迭代非线性最小二乘细化,可以进一步改善模型 sys1 实现的拟合度。这可以使用 ssest 命令来实现。我们使用 ssestOptions 命令设置了 ssest 的估计选项。这次还估计了参数协方差。
ssOpt = ssestOptions('EstimateCovariance',true,... 'WeightingFilter',n4Opt.WeightingFilter,... 'SearchMethod','lm',... % use Levenberg-Marquardt search method 'Display','on',... 'OutputWeight',eye(20)); sys2 = ssest(Gs, sys1, ssOpt); % estimate state-space model (this takes several minutes) Fit = sys2.Report.Fit.FitPercent'
Fit = 1×20
88.8715 88.6587 88.9388 89.8630 87.8597 88.1235 79.7016 82.5930 74.2458 82.6593 90.2663 88.7739 89.9033 89.0571 88.8040 88.2251 86.9307 87.5250 83.2249 82.8676
和以前一样,我们绘制最差和最佳拟合情况。我们还可视化了模型频率响应的 1-sd 置信域。
[~, Imin] = min(Fit); [~, Imax] = max(Fit); clf h = bodeplot(Gs([Imin, Imax],:), sys2([Imin, Imax],:), opt); showConfidence(h, 1) xlim([6.5 35]) title('Worst (top) and best (bottom) fits between data and refined model') grid on legend('Data', 'Model (sys2)')
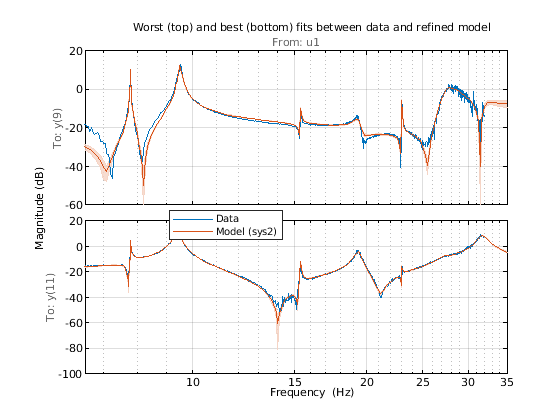
改进的状态空间模型 sys2 在 7–20 Hz 区域内能够很好地拟合 FRF。大多数共振位置的不确定性界限都很严格。我们估计了一个 24 阶模型,这意味着系统 sys2 中最多有 12 种振荡模式。使用 modalfit 命令获取这些模式的固有频率(以 Hz 为单位)。
f = Gs.Frequency/2/pi; % data frequencies (Hz) fn = modalfit(sys2, f, 12); % natural frequencies (Hz) disp(fn)
7.7720
7.7954
9.3176
9.4052
9.4919
15.3462
19.3281
23.0219
27.4035
28.6873
31.7036
64.2624
fn 中的值表明两个频率非常接近 7.8 Hz,三个频率接近 9.4 Hz。对这些频率附近的频率响应的检查表明,峰值位置在输出端有一点点偏移。可以通过更好地控制试验过程来消除这些差异,将输入带宽限制在以这些频率为中心的窄范围内进行直接时域辨识,或将单个振荡模式拟合到这些频率周围的频率响应。本例中没有探讨这些替代方案。
模态参数计算
我们现在可以使用模型 sys2 来提取模态参数。对 FRF 的检查表明大约有 10 个模态频率,大致在频率 [5 7 10 15 17 23 27 30] Hz 附近。我们可以使用 modalsd 命令来使这一评估更加具体,该命令可以检查模态参数在底层模型阶数改变时的稳定性。此操作需要很长时间。因此,生成的图表将直接作为图像插入。执行下面注释模块内的代码来重现该图。
FRF = permute(Gs.ResponseData,[3 1 2]); f = Gs.Frequency/2/pi; %{ figure pf = modalsd(FRF,f,fs,'MaxModes',20,'FitMethod','lsrf'); %}
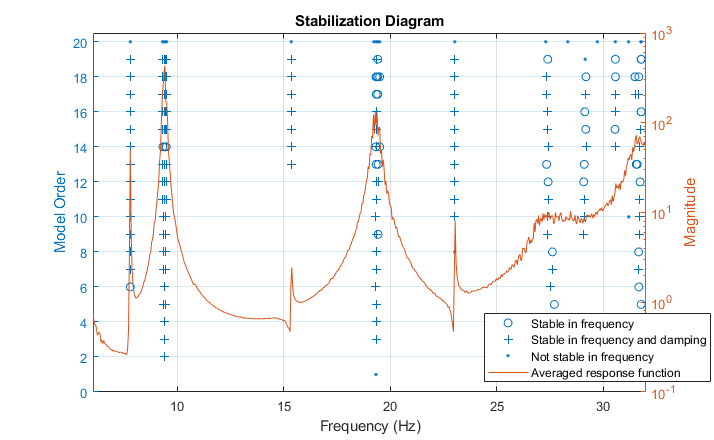
检查图表和 pf 值可以得到一份精确的真实固有频率列表:
Freq = [7.8 9.4 15.3 19.3 23.0 27.3 29.2 31.7];
我们使用 Freq 向量中的值作为从模型 sys2 中挑选最主要模式的指南。这是使用 modalfit 命令完成的。
[fn,dr,ms] = modalfit(sys2,f,length(Freq),'PhysFreq',Freq);fn 是固有频率(以赫兹为单位),dr 是相应的阻尼系数,ms 是列向量形式的归一化残差(每个固有频率一列)。在提取这些模态参数的过程中,仅使用模型的稳定、欠阻尼极点。ms 列仅包含具有正虚部的极点的极点。
模态形状可视化
为了直观地显示各种弯曲模式,我们需要上面提取的模态参数。此外,我们还需要有关测量点位置的信息。矩阵 AccePos 中记录了每个加速度计的这些位置(x-y 值):
AccelPos = [... % see figure 2 16.63 18.48; % nearest right of center 16.63 24.48; 27.90 22.22; 27.90 28.22; 37.17 25.97; 37.17 31.97; 46.44 29.71; 46.44 35.71; 55.71 33.46; 55.71 39.46; % farthest right -16.63 18.48; % nearest left of center -16.63 24.18; -27.90 22.22; -27.90 28.22; -37.17 25.97; -37.17 31.97; -46.44 29.71; -46.44 35.71; -55.71 33.46; -55.71 39.46]; % farthest left
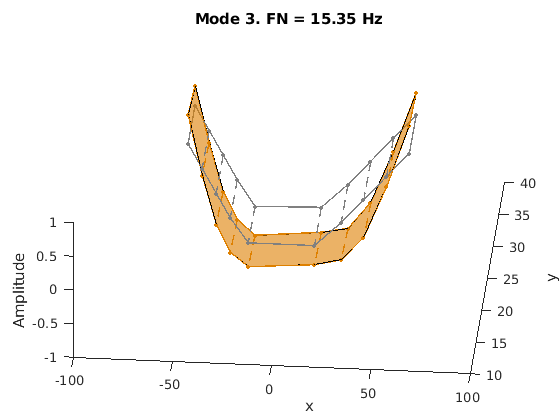
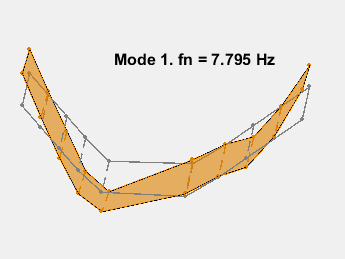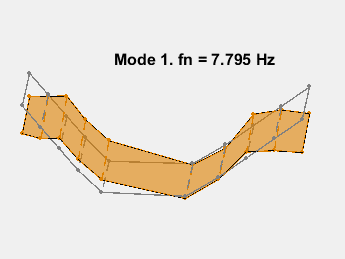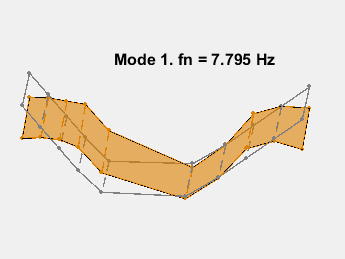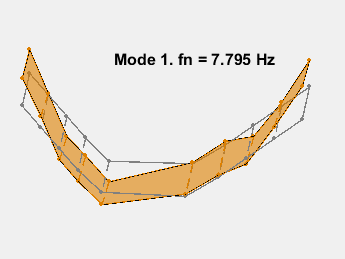
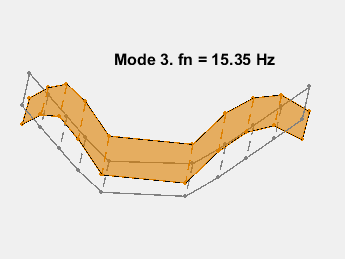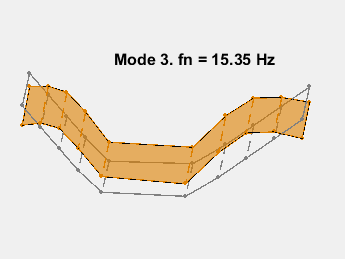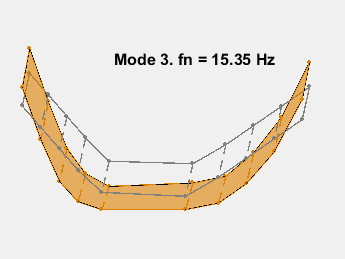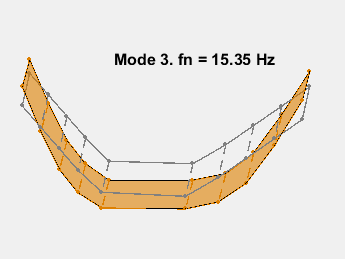
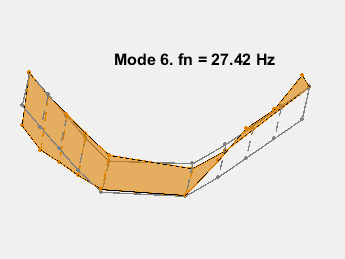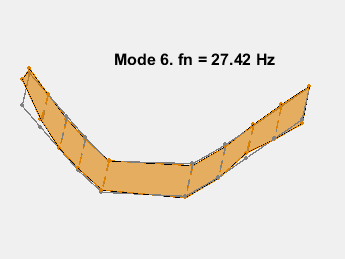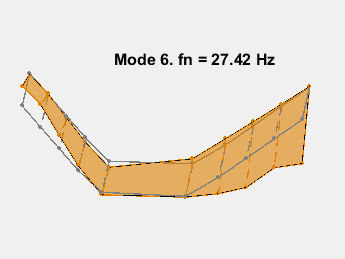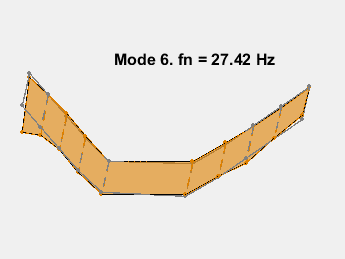
模式形状包含在矩阵 ms 中,其中每一列对应一个频率的形状。通过在传感器坐标上叠加模态振幅并改变模态固有频率的振幅来对模态进行动画处理。动画显示了无阻尼的弯曲。例如,考虑 15.3 Hz 的模式。
AnimateOneMode(3, fn, ms, AccelPos);
结论
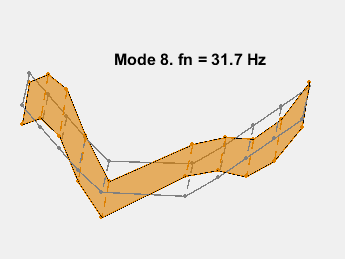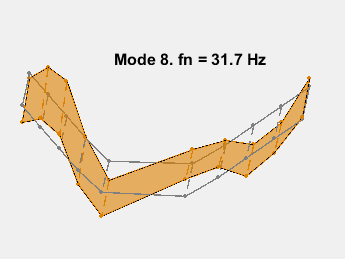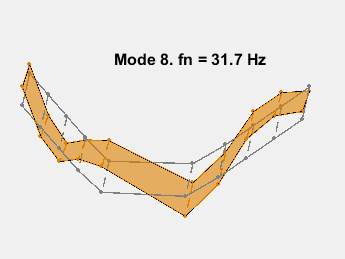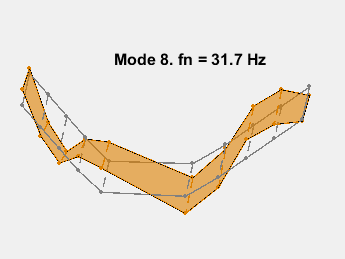
此示例展示了一种基于参数化模型辨识的模态参数估计方法。使用 24 阶状态空间模型,提取了 6~32Hz 频率范围内的 8 个稳定振荡模式。模态信息与加速度计位置的知识相结合,以可视化各种弯曲模式。下图显示了其中一些模式。
参考资料
[1] Gupta, Abhineet, Peter J. Seiler, and Brian P. Danowsky."Ground Vibration Tests on a Flexible Flying Wing Aircraft."AIAA Atmospheric Flight Mechanics Conference, AIAA SciTech Forum.(AIAA 2016-1753).
function AnimateOneMode(ModeNum, fn, ModeShapes, AccelPos) % Animate one mode. % ModeNum: Index of the mode. % Reorder the sensor locations for plotting so that a continuous, % non-intersecting curve is traced around the body of the aircraft. PlotOrder = [19:-2:11, 1:2:9, 10:-2:2, 12:2:20, 19]; Fwd = PlotOrder(1:10); Aft = PlotOrder(20:-1:11); x = AccelPos(PlotOrder,1); y = AccelPos(PlotOrder,2); xAft = AccelPos(Aft,1); yAft = AccelPos(Aft,2); xFwd = AccelPos(Fwd,1); yFwd = AccelPos(Fwd,2); wn = fn(ModeNum)*2*pi; % Mode frequency in rad/sec T = 1/fn(ModeNum); % Period of modal oscillation Np = 2.25; % Number of periods to simulate tmax = Np*T; % Simulate Np periods Nt = 100; % Number of time steps for animation t = linspace(0,tmax,Nt); ThisMode = ModeShapes(:,ModeNum)/max(abs(ModeShapes(:,ModeNum))); % normalized for plotting z0 = ThisMode(PlotOrder); zFwd = ThisMode(Fwd); zAft = ThisMode(Aft); clf col1 = [1 1 1]*0.5; xx = reshape([[xAft, xFwd]'; NaN(2,10)],[2 20]); yy = reshape([[yAft, yFwd]'; NaN(2,10)],[2 20]); plot3(x,y,0*z0,'-', x,y,0*z0,'.', xx(:), yy(:), zeros(40,1),'--',... 'Color',col1,'LineWidth',1,'MarkerSize',10,'MarkerEdgeColor',col1); xlabel('x') ylabel('y') zlabel('Amplitude') ht = max(abs(z0)); axis([-100 100 10 40 -ht ht]) view(5,55) title(sprintf('Mode %d. FN = %s Hz', ModeNum, num2str(fn(ModeNum),4))); % Animate by updating z-coordinates. hold on col2 = [0.87 0.5 0]; h1 = plot3(x,y,0*z0,'-', x,y,0*z0,'.', xx(:), yy(:), zeros(40,1),'--',... 'Color',col2,'LineWidth',1,'MarkerSize',10,'MarkerEdgeColor',col2); h2 = fill3(x,y,0*z0,col2,'FaceAlpha',0.6); hold off for k = 1:Nt Rot1 = cos(wn*t(k)); Rot2 = sin(wn*t(k)); z_t = real(z0)*Rot1 - imag(z0)*Rot2; zAft_t = real(zAft)*Rot1 - imag(zAft)*Rot2; zFwd_t = real(zFwd)*Rot1 - imag(zFwd)*Rot2; zz = reshape([[zAft_t, zFwd_t]'; NaN(2,10)],[2 20]); set(h1(1),'ZData',z_t) set(h1(2),'ZData',z_t) set(h1(3),'ZData',zz(:)) h2.Vertices(:,3) = z_t; pause(0.1) end end