本页采用了机器翻译。点击此处可查看最新英文版本。

在线递归最小二乘估计

此示例使用:

打开脚本

此示例显示如何实现在线递归最小二乘估计器。您估计内燃机的非线性模型并使用递归最小二乘法来检测发动机惯性的变化。

发动机模型

发动机模型包括节气门和歧管系统以及燃烧系统的非线性元件。模型输入是油门角度，模型输出是发动机转速 (rpm)。

open_system('iddemo_engine');
sim('iddemo_engine')

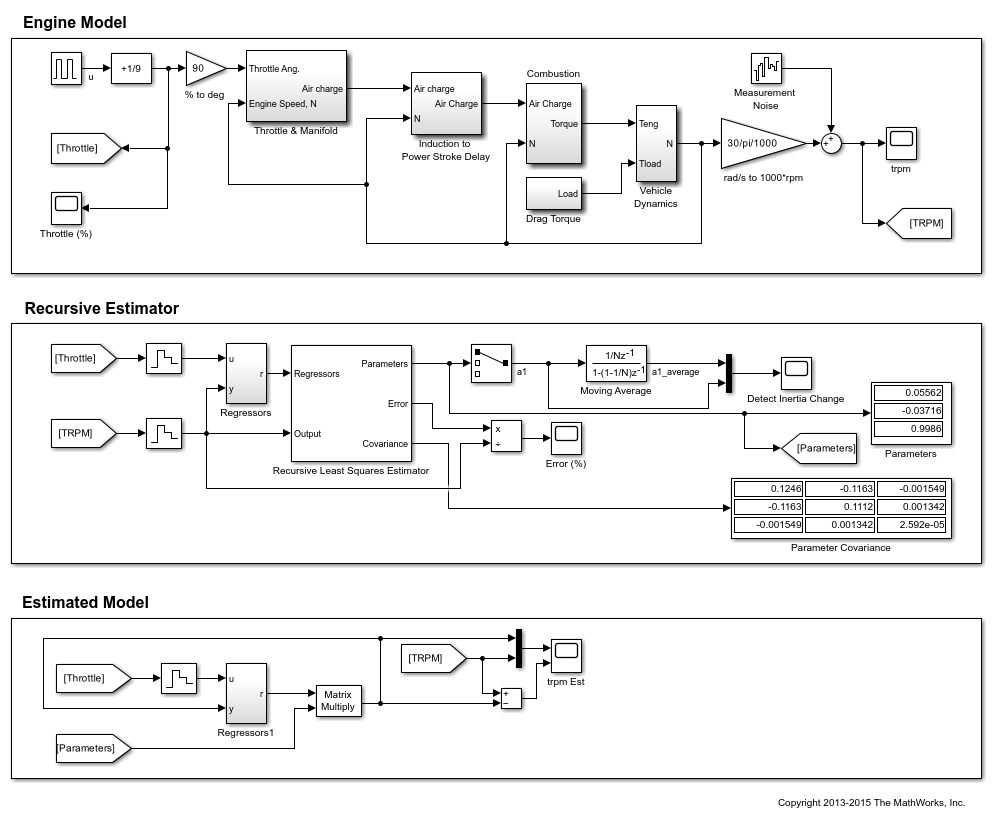
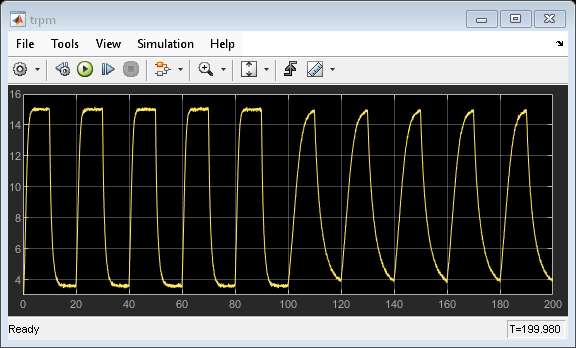
发动机模型设置了冲激序列来驱动油门角度从打开到关闭。发动机响应是非线性的，具体来说，油门打开和关闭时发动机转速响应时间是不同的。

在仿真进行到 100 秒时，发动机出现故障，导致发动机惯性增加（发动机惯性 J 在 iddemo_engine/Vehicle Dynamics 模块中建模）。惯性变化导致发动机在油门打开和关闭位置的响应时间增加。您使用在线递归最小二乘法来检测惯性变化。

open_system('iddemo_engine/trpm')

估计模型

发动机模型是一个阻尼二阶系统，具有输入和输出非线性，以解释不同油门位置下的不同响应时间。使用递归最小二乘模块来辨识对发动机进行建模的以下离散系统：

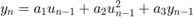
$y_n = a_1 u_{n-1} + a_2 u_{n-1}^2 + a_3 y_{n-1}$

由于估计模型没有明确包括惯性，我们预计 $a$ 值会随着惯性的变化而变化。我们使用变化的 $a$ 值来检测惯性变化。

该引擎具有高达 16Hz 的显著带宽。将估计器采样频率设置为 2*160Hz 或采样时间为 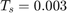$T_s = 0.003$ 秒。

Recursive Least Squares Estimator 模块设置

估计模型中的 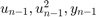$u_{n-1}, u_{n-1}^2, y_{n-1}$ 项是模型回归量，也是估计 $a$ 值的递归最小二乘模块的输入。您可以按照 iddemo_engine/Regressors 模块所示实现回归器。

open_system('iddemo_engine/Regressors');

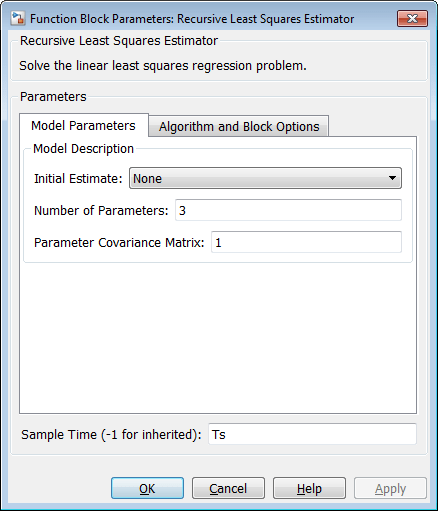
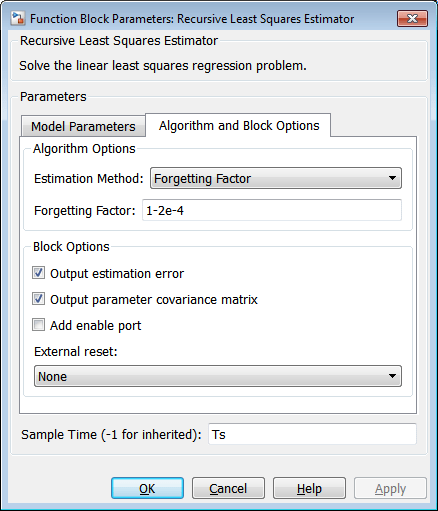
配置 Recursive Least Squares Estimator 模块：

  • Initial Estimate：无。默认情况下，软件使用值 1。

  • Number of parameters：3，每个 $a$ 回归系数一个。

  • Parameter Covariance Matrix：1，初始猜测的不确定性量为 1。具体来说，将估计的参数视为方差为 1 的随机变量。

  • Sample Time：$T_s$。

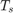点击 Algorithm and Block Options 来设置估计选项：

  • Estimation Method：Forgetting Factor

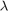  • Forgetting Factor：1-2e-4。由于估计的 $a$ 值预计会随着惯性而变化，因此将遗忘因子设置为小于 1 的值。选择 $\lambda$ = 1-2e-4，它对应于内存时间常数 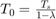$T_0 = \frac{T_s}{1-\lambda}$ 或 15 秒。15 秒的记忆时间确保了油门打开和关闭位置的重要数据均可用于估计，因为位置每 10 秒就会发生变化。

  • 选中 Output estimation error 复选框。您使用此模块输出来验证估计。

  • 选中 Output parameter covariance matrix 复选框。您使用此模块输出来验证估计。

  • 清除 Add enable port 复选框。

  • External reset：None。

验证估计模型

Recursive Least Squares Estimator 模块的 Error 输出为估计模型提供了一步前进误差。该误差小于 5%，表明对于一步预测，估计的模型是准确的。

open_system('iddemo_engine/Error (%)')

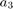参数协方差矩阵的对角线给出了 $a_n$ 参数的方差。$a_3$ 方差相对于参数值较小，表明对估计值的信心良好。相反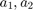，$a_1, a_2$ 方差相对于参数值较大，表明对这些值的置信度较低。

虽然较小的估计误差和协方差使人们相信模型估计正确，但它受到限制，因为误差是一个提前一步的预测器。更严格的检查是在仿真模型中使用估计模型并与实际模型输出进行比较。Simulink® 模型的 Estimated Model 部分实现了这一点。

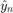Regressors1 模块与递归估计器中使用的 Regressors 模块相同。唯一的区别是 y 信号不是从工厂测量的，而是从估计模型的输出反馈的。回归模块的输出乘以估计的 $a_n$ 值，得出 $\hat{y}_n$ 发动机转速的估计值。

open_system('iddemo_engine/trpm Est')

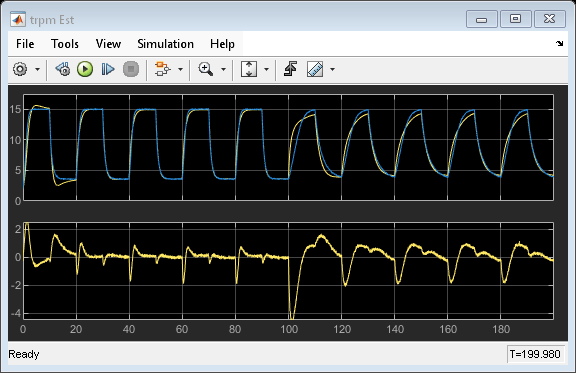
估计的模型输出与模型输出相当匹配。稳态值接近，瞬态行为略有不同，但差别不大。请注意，100 秒后，当发动机惯性发生变化时，估计的模型输出与模型输出略有不同。这意味着所选的回归量无法在惯性改变后很好地捕获模型的行为。这也表明系统行为发生了改变。

估计的模型输出与较低的一步前进误差和参数协方差相结合，使我们对递归估计器充满信心。

检测发动机惯性的变化

发动机模型的设置是为了在仿真中引入 100 秒的惯性变化。递归估计器可用于检测惯性的变化。

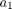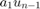递归估计器大约需要 50 秒才能收敛到一组初始参数值。为了检测惯性变化，我们检查影响估计模型的 $a_1 u_{n-1}$ 项的 $a_1$ 模型系数。

open_system('iddemo_engine/Detect Inertia Change')

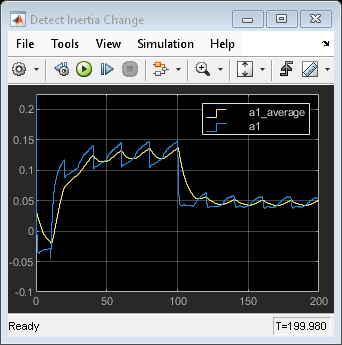
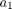$a_1$ 的协方差为 0.05562，相对于参数值 0.1246 较大，表明估计值的置信度较低。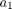$a_1$ 的时间图显示了协方差较大的原因。具体来说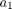，$a_1$ 随着油门位置的变化而变化，这表明估计模型不够丰富，无法完全捕获不同油门位置的不同上升时间，需要调整 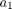$a_1$。然而，我们可以利用它来辨识惯性变化，因为 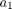$a_1$ 的值随着惯性的变化而变化。您可以在 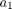$a_1$ 参数的移动平均值上使用阈值检测器来检测引擎惯性的变化。

bdclose('iddemo_engine')