Reconstructing an Image from Projection Data

Create Head Phantom

The test image is the Shepp-Logan head phantom which can be generated using the function phantom. The phantom image illustrates many qualities that are found in real-world tomographic imaging of human heads. The bright elliptical shell along the exterior is analogous to a skull and the many ellipses inside are analogous to brain features or tumors.

P = phantom(256);
imshow(P)

Parallel Beam - Calculate Synthetic Projections

Calculate synthetic projections using parallel-beam geometry and vary the number of projection angles. For each of these calls to radon, the output is a matrix in which each column is the Radon transform for one of the angles in the corresponding theta.

theta1 = 0:10:170; 
[R1,~] = radon(P,theta1); 
num_angles_R1 = size(R1,2)

num_angles_R1 = 
18

theta2 = 0:5:175;  
[R2,~] = radon(P,theta2);
num_angles_R2 = size(R2,2)

num_angles_R2 = 
36

theta3 = 0:2:178;  
[R3,xp] = radon(P,theta3); 
num_angles_R3 = size(R3,2)

num_angles_R3 = 
90

Note that for each angle, the projection is computed at N points along the xp-axis, where N is a constant that depends on the diagonal distance of the image such that every pixel will be projected for all possible projection angles.

N_R1 = size(R1,1)

N_R1 = 
367

N_R2 = size(R2,1)

N_R2 = 
367

N_R3 = size(R3,1)

N_R3 = 
367

So, if you use a smaller head phantom, the projection needs to be computed at fewer points along the xp-axis.

P_128 = phantom(128);
[R_128,xp_128] = radon(P_128,theta1);
N_128 = size(R_128,1)

N_128 = 
185

Display the projection data R3. Some of the features of the original phantom image are visible in the image of R3. The first column of R3 corresponds to a projection at 0 degrees, which is integrating in the vertical direction. The centermost column corresponds to a projection at 90 degrees, which is integrating in the horizontal directions. The projection at 90 degrees has a wider profile than the projection at 0 degrees due to the large vertical semi-axis of the outermost ellipse of the phantom.

imagesc(theta3,xp,R3)
colormap(hot)
colorbar
xlabel('Parallel Rotation Angle - \theta (degrees)'); 
ylabel('Parallel Sensor Position - x\prime (pixels)');

Parallel Beam - Reconstruct Head Phantom from Projection Data

Match the parallel rotation-increment, dtheta, in each reconstruction with that used above to create the corresponding synthetic projections. In a real-world case, you would know the geometry of your transmitters and sensors, but not the source image, P.

The following three reconstructions (I1, I2, and I3) show the effect of varying the number of angles at which projections are made. For I1 and I2 some features that were visible in the original phantom are not clear. Specifically, look at the three ellipses at the bottom of each image. The result in I3 closely resembles the original image, P.

Notice the significant artifacts present in I1 and I2. To avoid these artifacts, use a larger number of angles.

% Constrain the output size of each reconstruction to be 
% the same as the size of the original image, |P|.
output_size = max(size(P));

dtheta1 = theta1(2) - theta1(1);
I1 = iradon(R1,dtheta1,output_size);

dtheta2 = theta2(2) - theta2(1);
I2 = iradon(R2,dtheta2,output_size);

dtheta3 = theta3(2) - theta3(1);
I3 = iradon(R3,dtheta3,output_size);

figure
montage({I1,I2,I3},'Size',[1 3])
title(['Reconstruction from Parallel Beam Projection ' ...
    'with 18, 24, and 90 Projection Angles'])

Fan Beam - Calculate Synthetic Projections

Calculate synthetic projections using fan-beam geometry and vary the 'FanSensorSpacing'.

D = 250; 
dsensor1 = 2;
F1 = fanbeam(P,D,'FanSensorSpacing',dsensor1);

dsensor2 = 1;
F2 = fanbeam(P,D,'FanSensorSpacing',dsensor2);

dsensor3 = 0.25;
[F3,sensor_pos3,fan_rot_angles3] = fanbeam(P,D, ...
    'FanSensorSpacing',dsensor3);

Display the projection data F3. Notice that the fan rotation angles range from 0 to 360 degrees and the same patterns occur at an offset of 180 degrees because the same features are being sampled from both sides. You can correlate features in this image of fan-beam projections with the same features in the image of parallel-beam projections, above.

imagesc(fan_rot_angles3,sensor_pos3,F3)
colormap(hot)
colorbar
xlabel('Fan Rotation Angle (degrees)')
ylabel('Fan Sensor Position (degrees)')

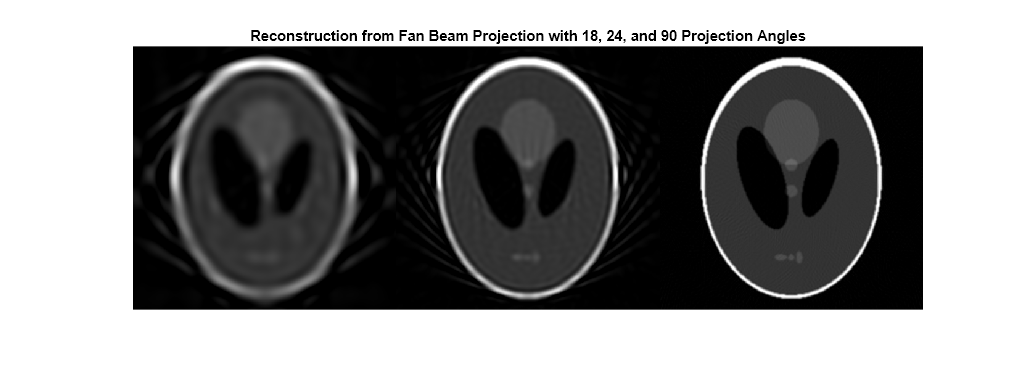
Fan Beam - Reconstruct Head Phantom from Projection Data

Match the fan-sensor-spacing in each reconstruction with that used to create each of the synthetic projections. In a real-world case, you would know the geometry of your transmitters and sensors, but not the source image, P.

Changing the value of the 'FanSensorSpacing' effectively changes the number of sensors used at each rotation angle. For each of these fan-beam reconstructions, the same rotation angles are used. This is in contrast to the parallel-beam reconstructions which each used different rotation angles.

Note that 'FanSensorSpacing' is only one parameter of several that you can control when using fanbeam and ifanbeam. You can also convert back and forth between parallel- and fan-beam projection data using the functions fan2para and para2fan.

Ifan1 = ifanbeam(F1,D,'FanSensorSpacing',dsensor1, ...
    'OutputSize',output_size);
Ifan2 = ifanbeam(F2,D,'FanSensorSpacing',dsensor2, ...
    'OutputSize',output_size);
Ifan3 = ifanbeam(F3,D,'FanSensorSpacing',dsensor3, ...
    'OutputSize',output_size);

montage({Ifan1,Ifan2,Ifan3},'Size',[1 3])
title(['Reconstruction from Fan Beam Projection with '...
    '18, 24, and 90 Projection Angles'])