breusing
Breusing Harmonic Mean Projection
Classification
Azimuthal
Identifier
breusing
Graticule
The graticule described is for the polar aspect.
Meridians: Equally spaced straight lines intersecting at the central pole.
Parallels: Unequally spaced circles centered on the central pole. The opposite hemisphere cannot be shown. Spacing increases (slightly) away from the central pole.
Poles: The central pole is a point, while the opposite pole cannot be shown.
Symmetry: About any meridian.
Features
This is a harmonic mean between a Stereographic and Lambert Equal-Area Azimuthal projection. It is not equal-area, equidistant, or conformal. There is no point at which scale is accurate in all directions. The primary feature of this projection is that it is minimum error—distortion is moderate throughout.
Parallels
There are no standard parallels for azimuthal projections.
Remarks
F. A. Arthur Breusing developed a geometric mean version of this projection in 1892. A. E. Young modified this to the harmonic mean version presented here in 1920. This projection is virtually indistinguishable from the Airy Minimum Error Azimuthal projection, presented by George Airy in 1861.
This implementation of the Breusing harmonic mean projection is applicable only for coordinates that are referenced to a sphere.
Example
landareas = shaperead('landareas.shp','UseGeoCoords',true);
axesm ('breusing', 'Frame', 'on', 'Grid', 'on');
geoshow(landareas,'FaceColor',[1 1 .5],'EdgeColor',[.6 .6 .6]);
tissot;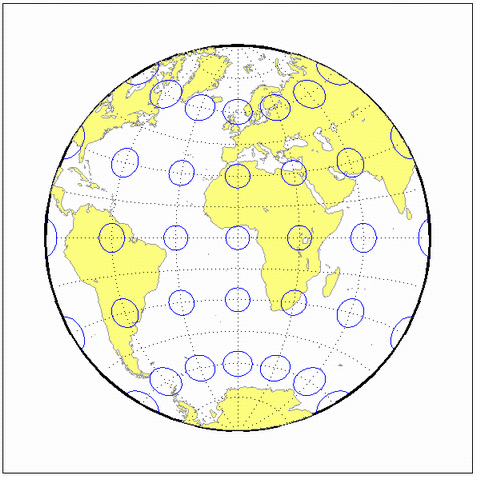
Version History
Introduced before R2006a