Equal-Areas in Geographic Statistics

A common error in applying two-dimensional statistics to geographic data lies in ignoring equal-area treatment. It is often necessary to bin data to statistically analyze it. In a Cartesian plane, this is easily done by dividing the space into equal x-y squares. The geographic equivalent of this is to bin up the data in equal latitude-longitude squares. Since such squares at high latitudes cover smaller areas than their low-latitude counterparts, the observations in these regions are underemphasized. The result can be conclusions that are biased toward the equator.

Geographic Histograms

The geographic histogram function histr allows you to display binned-up geographic observations. The histr function results in equirectangular binning. Each bin has the same angular measurement in both latitude and longitude, with a default measurement of 1 degree. The center latitudes and longitudes of the bins are returned, as well as the number of observations per bin:

[binlat,binlon,num] = histr(lats,lons)

As previously noted, these equirectangular bins result in counting bias toward the equator. Here is a display of the one-degree-by-one-degree binning of approximately 5,000 random data points in Russia. The relative size of the circles indicates the number of observations per bin:

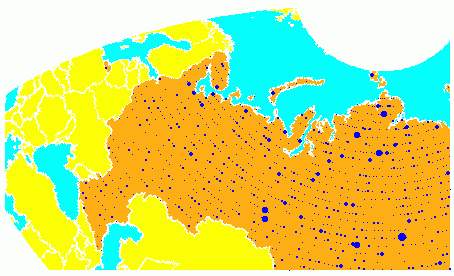
One-degree-by-one-degree binning of random data points in Russia

This is a portion of the whole map, displayed in an equal-area Bonne projection. The first step in creating data displays without area bias is to choose an equal-area projection. The proportionally sized symbols are a result of the specialized display function scatterm.

You can eliminate the area bias by adding a fourth output argument to histr, that will be used to weight each bin's observation by that bin's area:

[binlat,binlon,num,wnum] = histr(lats,lons)

The fourth output is the weighted observation count. Each bin's observation count is divided by its normalized area. Therefore, a high-latitude bin will have a larger weighted number than a low-latitude bin with the same number of actual observations. The same data and bins look much different when they are area-weighted:

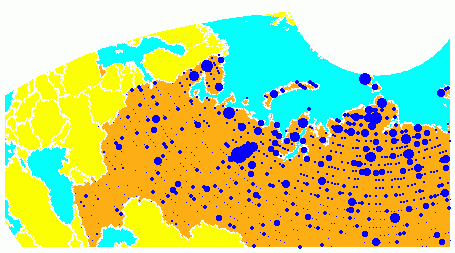
The same map of Russia, this time with area-weighted bins

Notice that there are larger symbols to the north in this display. The previous display suggested that the data was relatively uniformly distributed. When equal-area considerations are included, it is clear that the data is skewed to the north. In fact, the data used is northerly skewed, but a simple equirectangular handling failed to demonstrate this.

The histr function, therefore, does provide for the display of area-weighted data. However, the actual bins used are of varying areas. Remember, the one-degree-by-one-degree bin near a pole is much smaller than its counterpart near the equator.

The hista function provides for actual equal-area bins.

Converting to an Equal-Area Coordinate System

The actual data itself can be converted to an equal-area coordinate system for analysis with other statistical functions. It is easy to convert a collection of geographic latitude-longitude points to an equal-area x-y Cartesian coordinate system. The grn2eqa function applies the same transformation used in calculating the Equal-Area Cylindrical projection:

[x,y] = grn2eqa(lat,lon)

For each geographic lat - lon pair, an equal-area x - y is returned. The variables x and y can then be operated on under the equal-area assumption, using a variety of two-dimensional statistical techniques. Tools for such analysis can be found in the Statistics and Machine Learning Toolbox™ software and elsewhere. The results can then be converted back to geographic coordinates using the eqa2grn function:

[lat,lon] = eqa2grn(x, y)

Remember, when converting back and forth between systems, latitude corresponds to y and longitude corresponds to x.