使用 FFT 进行多项式插值

使用快速傅里叶变换 (FFT) 来估算用于对一组数据进行插值的三角函数多项式的系数。

数学中的 FFT

FFT 算法通常与信号处理应用相关，但也可以在数学领域更广泛地用作快速计算工具。例如，通常通过解算简单的线性系统来计算用于对一组数据进行插值的 n 次多项式 $c_{1} x^{n} + c_{2} x^{n - 1} + ... + c_{n} x + c_{n + 1}$ 的系数 c_i。在 19 世纪初研究小行星轨道时，卡尔·弗里德里希·高斯发现了一种数学捷径，即通过将问题分解为多个较小的子问题，然后将结果合并来计算多项式插值的系数。他的方法等同于估算其数据的离散傅里叶变换。

小行星数据插值

打开实时脚本

在高斯的论文中，他描述了一种估算小行星智神星轨道的方法。他从以下 12 个二维数据点 x 和 y 开始。

x = 0:30:330;
y = [408 89 -66 10 338 807 1238 1511 1583 1462 1183 804];
plot(x,y,'ro')
xlim([0 360])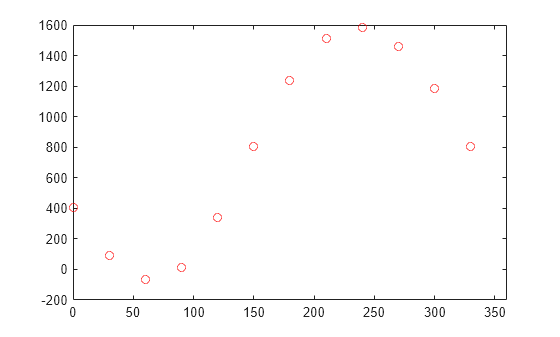

Figure contains an axes object. The axes contains a line object which displays its values using only markers.

高斯使用以下形式的三角函数多项式为小行星的轨道建模。

$\begin{array}{rcl} y = a_{0} & + & a_{1} \cos (2 π (x / 360)) + b_{1} \sin (2 π (x / 360)) \\ a_{2} \cos (2 π (2 x / 360)) + b_{2} \sin (2 π (2 x / 360)) \\ \dots \\ a_{5} \cos (2 π (5 x / 360)) + b_{5} \sin (2 π (5 x / 360)) \\ a_{6} \cos (2 π (6 x / 360)) \end{array}$

使用 fft 计算多项式的系数。

m = length(y);
n = floor((m+1)/2);
z = fft(y)/m;

a0 = z(1); 
an = 2*real(z(2:n));
a6 = z(n+1);
bn = -2*imag(z(2:n));

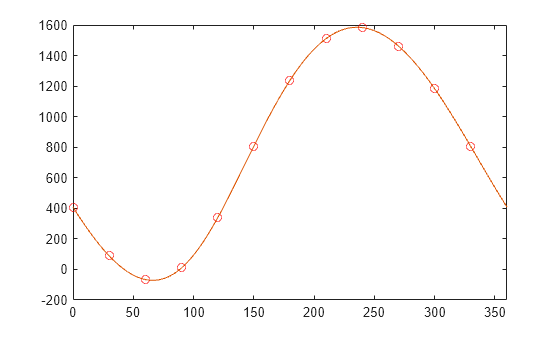
在原始数据点上绘制插值多项式。

hold on
px = 0:0.01:360;
k = 1:length(an);
py = a0 + an*cos(2*pi*k'*px/360) ...
        + bn*sin(2*pi*k'*px/360) ...
        + a6*cos(2*pi*6*px/360); 

plot(px,py)

Figure contains an axes object. The axes object contains 2 objects of type line. One or more of the lines displays its values using only markers

参考

[1] Briggs, W. and V.E. Henson. The DFT: An Owner's Manual for the Discrete Fourier Transform. Philadelphia: SIAM, 1995.

[2] Gauss, C. F. “Theoria interpolationis methodo nova tractata.” Carl Friedrich Gauss Werke. Band 3. Göttingen: Königlichen Gesellschaft der Wissenschaften, 1866.

[3] Heideman M., D. Johnson, and C. Burrus. “Gauss and the History of the Fast Fourier Transform.” Arch. Hist. Exact Sciences. Vol. 34. 1985, pp. 265–277.

[4] Goldstine, H. H. A History of Numerical Analysis from the 16th through the 19th Century. Berlin: Springer-Verlag, 1977.

另请参阅

fft

主题

傅里叶变换