使用高精度算术求解近整数

此示例使用:

本示例说明如何使用 Symbolic Math Toolbox™ 中的可变精度算术求解近整数或非常接近整数的数。在本示例中，您需要搜索 exp(pi*sqrt(n)) 或 exp(pi*n) 形式的近整数，其中 n 为 1, ..., 200 的整数。

默认情况下，MATLAB® 使用 16 位数字的精度。如果需要更高的精度，请使用 Symbolic Math Toolbox 中的 vpa 函数。vpa 提供可变精度，在计算数字时可以提高精度。

首先，假设有一个著名的近整数示例 [2]，即实数 exp(pi*sqrt(163))。将此实数创建为一个精确的符号数。

r = exp(pi*sqrt(sym(163)))

 
r =
 
exp(pi*163^(1/2))

使用 vpa 以可变精度算术计算此数字。默认情况下，vpa 将值计算到 32 位有效数字。

f = vpa(r)

 
f =
 
262537412640768743.99999999999925

您可以使用 digits 函数更改有效数字的位数。将同一个数字计算到 25 位有效数字。

digits(25)
f = vpa(r)

 
f =
 
262537412640768744.0

此数字非常接近整数。找到此实数与其最接近的整数之间的差值。使用 vpa 将该差异计算到 25 位有效数字。

dr = vpa(round(r)-r)

 
dr =
 
0.0000000000007425171588693046942353249

搜索 exp(pi*sqrt(n)) 形式的近整数，其中 n 为 1, ..., 200 的整数。将这些数字创建为精确的符号数。

A = exp(pi*sqrt(sym(1:200)));

将有效数字的位数设置为 exp(pi*sqrt(200)) 的整数部分的位数，再加上 20 位。

d = log10(A(end));
digits(ceil(d)+20)

计算这些数字序列与其最接近的整数之间的差值。找到舍入误差小于 0.0001 的近整数。以精确符号形式显示这些近整数。

B = vpa(round(A)-A);
A_nearint = A(abs(B)<0.0001)'

 
A_nearint =
 
 exp(pi*37^(1/2))
 exp(pi*58^(1/2))
 exp(pi*67^(1/2))
exp(pi*163^(1/2))

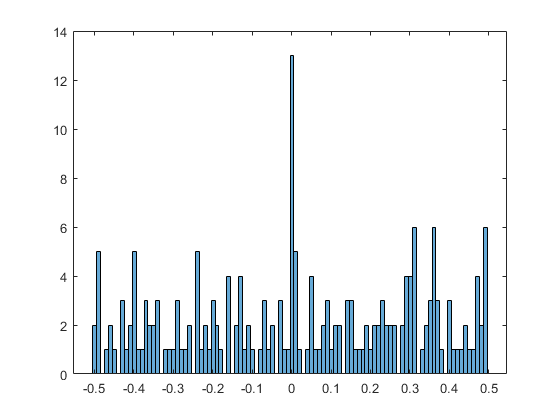
绘制差值直方图。其分布显示接近零的差值很多，其中 exp(pi*sqrt(n)) 形式的数为近整数。

histogram(double(B),100)

搜索 exp(pi*n) 形式的近整数，其中 n 为 1, ..., 200 的整数。将这些数字创建为精确的符号数。

A = exp(pi*sym(1:200));

将有效数字的位数设置为 exp(pi*200) 的整数部分的位数，再加上 20 位。

d = log10(A(end));
digits(ceil(d)+20)

计算这些数字序列与其最接近的整数之间的差值。找到舍入误差小于 0.0001 的近整数。结果是一个空的 sym 数组，意味着此序列中没有满足此条件的数字。

B = vpa(round(A)-A);
A_nearint = A(abs(B)<0.0001)

 
A_nearint =
 
Empty sym: 1-by-0

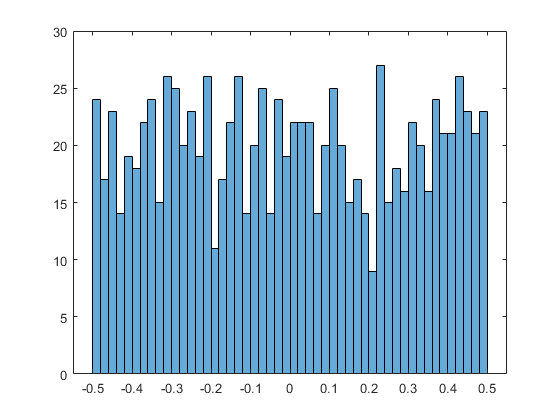
绘制差值直方图。直方图的分布相对均匀，说明 exp(pi*n) 这种形式不会生成很多的近整数。对于此特定示例而言，说明没有误差小于 0.0001 的近整数。

histogram(double(B),100)

最后，恢复 32 位有效数字默认精度以进行进一步的计算。

digits(32)