Main Content

对复数值数据进行模型拟合

打开脚本

此示例说明如何对复数值数据执行非线性拟合。虽然大多数 Optimization Toolbox™ 求解器和算法只能处理实数值数据，但最小二乘求解器和 fsolve 可以处理无约束问题的实数值和复数值数据。目标函数必须为复函数意义上的解析函数。

使用复数数据时，请不要将 FunValCheck 选项设置为 'on'。求解器出错。请不要将 'interior-point' 算法与 lsqcurvefit 或 lsqnonlin 结合使用；此算法主要用于处理约束，但尚未经过验证是否能够处理复数数据。

数据模型

以下数据模型是一个简单的指数：

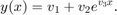
$$y(x) = v_1 + v_2 e^{v_3 x}.$$

$x$ 是输入数据，$y$ 是响应，$v$ 是由系数组成的复数值向量。目标是基于 $x$ 和噪声观测值 $y$ 估计 $v$。该数据模型是解析模型，因此您可以将它用于复杂的求解。

含噪人工数据

为模型生成人工数据。将复系数向量 $v$ 设为 [2;3+4i;-.5+.4i]。将观测值 $x$ 设为指数分布。向响应 $y$ 添加复数值噪声。

rng default % for reproducibility
N = 100; % number of observations
v0 = [2;3+4i;-.5+.4i]; % coefficient vector
xdata = -log(rand(N,1)); % exponentially distributed
noisedata = randn(N,1).*exp((1i*randn(N,1))); % complex noise
cplxydata = v0(1) + v0(2).*exp(v0(3)*xdata) + noisedata;

拟合模型以恢复系数向量

数据模型预测的响应与观测值之间的差异（$x$ 为 xdata，$y$ 为响应 cplxydata）为：

objfcn = @(v)v(1)+v(2)*exp(v(3)*xdata) - cplxydata;

使用 lsqnonlin 或 lsqcurvefit 对数据进行模型拟合。此示例首先使用 lsqnonlin。

opts = optimoptions(@lsqnonlin,'Display','off');
x0 = (1+1i)*[1;1;1]; % arbitrary initial guess
[vestimated,resnorm,residuals,exitflag,output] = lsqnonlin(objfcn,x0,[],[],opts);
vestimated,resnorm,exitflag,output.firstorderopt

vestimated =

   2.1582 + 0.1351i
   2.7399 + 3.8012i
  -0.5338 + 0.4660i


resnorm =

  100.9933


exitflag =

     3


ans =

    0.0018

lsqnonlin 将复系数向量恢复为一个有效数字。残差范数相当大，表明噪声使模型无法拟合所有观测值。退出标志是 3 而不是首选的 1，因为一阶最优性测度大约是 1e-3，未低于 1e-6。

替代方法：使用 lsqcurvefit

要使用 lsqcurvefit 进行拟合，请将模型编写为只提供响应，而不是响应减去响应数据。

objfcn = @(v,xdata)v(1)+v(2)*exp(v(3)*xdata);

使用 lsqcurvefit 选项和语法。

opts = optimoptions(@lsqcurvefit,opts); % reuse the options
[vestimated,resnorm] = lsqcurvefit(objfcn,x0,xdata,cplxydata,[],[],opts)

vestimated =

   2.1582 + 0.1351i
   2.7399 + 3.8012i
  -0.5338 + 0.4660i


resnorm =

  100.9933

结果与使用 lsqnonlin 得到的结果匹配，因为底层算法是相同的。使用您认为更方便的求解器。

替代方法：拆分实部和虚部

为了包括边界，或简单地完全保持在实数值内，您可以将系数的实部和复部拆分成单独的变量。对于此问题，拆分系数如下：

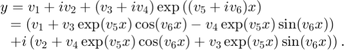
$$ \begin{array}{l}
y = {v_1} + i{v_2} + ({v_3} + i{v_4})\exp \left( {({v_5} + i{v_6})x} \right)\\
\ \ = \left( {{v_1} + {v_3}\exp ({v_5}x)\cos ({v_6}x) - {v_4}\exp ({v_5}x)\sin ({v_6}x)} \right)\\
\ \ + i \left( {{v_2} + {v_4}\exp ({v_5}x)\cos ({v_6}x) + {v_3}\exp ({v_5}x)\sin ({v_6}x)} \right).
\end{array}$$

编写 lsqcurvefit 的响应函数。

function yout = cplxreal(v,xdata)

yout = zeros(length(xdata),2); % allocate yout

expcoef = exp(v(5)*xdata(:)); % magnitude
coscoef = cos(v(6)*xdata(:)); % real cosine term
sincoef = sin(v(6)*xdata(:)); % imaginary sin term
yout(:,1) = v(1) + expcoef.*(v(3)*coscoef - v(4)*sincoef);
yout(:,2) = v(2) + expcoef.*(v(4)*coscoef + v(3)*sincoef);

将以下代码保存为 MATLAB® 路径下的文件 cplxreal.m。

将响应数据拆分为实部和虚部。

ydata2 = [real(cplxydata),imag(cplxydata)];

系数向量 v 现在有六个维度。将其初始化为全部为一的值，并使用 lsqcurvefit 求解问题。

x0 = ones(6,1);
[vestimated,resnorm,residuals,exitflag,output] = ...
    lsqcurvefit(@cplxreal,x0,xdata,ydata2);
vestimated,resnorm,exitflag,output.firstorderopt

Local minimum possible.

lsqcurvefit stopped because the final change in the sum of squares relative to 
its initial value is less than the value of the function tolerance.


vestimated =

    2.1582
    0.1351
    2.7399
    3.8012
   -0.5338
    0.4660


resnorm =

  100.9933


exitflag =

     3


ans =

    0.0018

将六元素向量 vestimated 解释为三元素复数向量，您会发现该解实际上与之前的解相同。

相关主题