基于求解器的边界约束二次规划

问题定义

考虑搭建一个马戏团帐篷来覆盖一块方形场地。帐篷有五根杆子，上面覆盖着厚重的弹性材料。问题在于找到帐篷的自然形状。将形状建模为位置 p 处帐篷的高度 x(p)。

重物被提升到高度 x 的势能为 cx，其中 c 为常数，与物的重量成比例。对于这个问题，选择 c = 1/3000。

一块材料 $$E_{stretch}$$ 的弹性势能大约与材料高度的二阶导数乘以高度成正比。您可以通过 5 点有限差分近似来近似二阶导数（假设有限差分步骤的大小为 1）。让 $$\Delta x$$ 表示在第一个坐标方向上移动 1，让 $$\Delta y$$ 表示在第二个坐标方向上移动 1。

帐篷的自然形状使总势能最小化。通过离散化问题，您会发现要最小化的总势能是 $$E_{stretch}(p)$$ + cx(p) 的所有位置 p 的总和。

该势能是变量 x 的二次表达式。

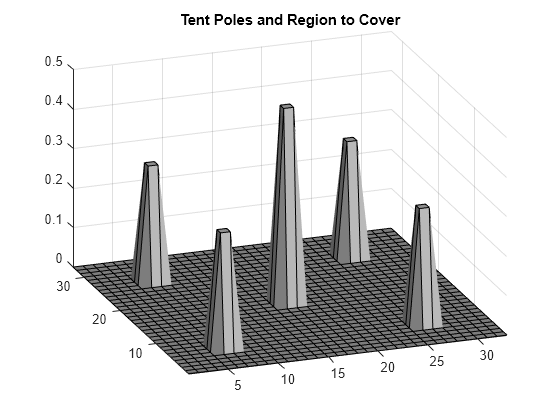
指定边界条件，即帐篷边缘的高度为零。帐篷杆的横截面为 1×1 单位，帐篷的总尺寸为 33×33 单位。指定每根杆的高度和位置。绘制方形地块区域和帐篷杆。

height = zeros(33);
height(6:7,6:7) = 0.3;
height(26:27,26:27) = 0.3;
height(6:7,26:27) = 0.3;
height(26:27,6:7) = 0.3;
height(16:17,16:17) = 0.5;
colormap(gray);
surfl(height)
axis tight
view([-20,30]);
title('Tent Poles and Region to Cover')

创建边界条件

height 矩阵定义了解 x 的下界。为了将解限制为边界上的零，请将上界 ub 设置为边界上的零。

boundary = false(size(height));
boundary([1,33],:) = true;
boundary(:,[1,33]) = true;
ub = inf(size(boundary)); % No upper bound on most of the region
ub(boundary) = 0;

创建目标函数矩阵

quadprog 问题表示为最小化

$$\frac{1}{2}{x}^{T}Hx+f^{T}x$$.

在这种情况下，线性项 $$f^{T}x$$ 对应于材料高度的势能。因此，为 x 的每个分量指定 f = 1/3000。

f = ones(size(height))/3000;

使用 delsq 函数创建表示 $$E_{stretch}$$ 的有限差分矩阵。delsq 函数返回一个稀疏矩阵，其中条目 4 和 -1 与 $$E_{stretch}(p)$$ 公式中的条目 4 和 -1 相对应。将返回的矩阵乘以 2，让 quadprog 使用 $$E_{stretch}$$ 给出的能量函数求解二次规划。

H = delsq(numgrid('S',33+2))*2;

查看矩阵 H 的结构。矩阵对 x(:) 进行操作，也就是说矩阵 x 通过线性索引转换为向量。

spy(H);
title('Sparsity Structure of Hessian Matrix');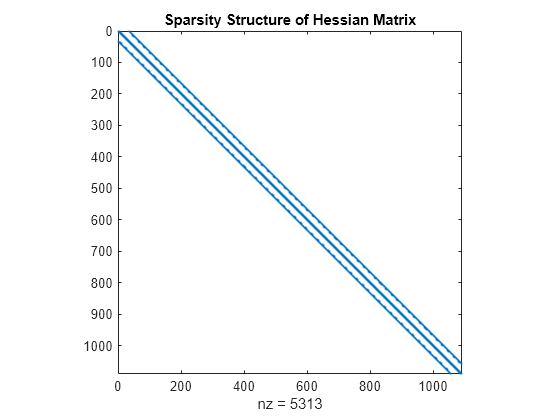

运行优化求解器

通过调用 quadprog 求解问题。

x = quadprog(H,f,[],[],[],[],height,ub);

Minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

<stopping criteria details>

对解进行绘图

将解 x 重塑为矩阵 S。然后绘制解。

S = reshape(x,size(height));
surfl(S);
axis tight;
view([-20,30]);