混合整数二次规划投资组合优化：基于问题

问题概要

根据马科维茨所述 ("Portfolio Selection," J. Finance Volume 7, Issue 1, pp. 77-91, March 1952)，您可以将许多投资组合优化问题表达为二次规划问题。假设您有包含 N 项的一组资产并希望选择一个投资组合，其中 $$x(i)$$ 是您在 $$i$$ 资产中的投资比例。如果您知道每项资产平均回报的向量 $$r$$，以及回报的协方差矩阵 $$Q$$，则对于给定的风险厌恶水平 λ$$\lambda$$，您需要最大化风险调整后的预期回报：

quadprog 求解器用于求解此二次规划问题。但是，除了简单的二次规划问题之外，您还可能希望以多种方式限制投资组合，例如：

您无法在 quadprog 中包含这些约束。困难在于约束的离散性。此外，虽然混合整数线性规划求解器处理离散约束，但它不处理二次目标函数。

此示例构造一系列满足约束的 MILP 问题，这些问题越来越逼近二次目标函数。虽然这种方法适用于此示例，但它可能不适用于不同问题或约束类型。

首先对约束进行建模。

对离散约束建模

$$x$$ 是资产配置比例的向量，对于每个 $$i$$，$$0\le x(i)\le 1$$。要对投资组合中的资产数量进行建模，您需要指示变量 $$v$$，满足当 $$x(i)=0$$ 时 $$v(i)=0$$，当 $$x(i)>0$$ 时 $$v(i)=1$$。要获得满足此约束的变量，请将 $$v$$ 向量设置为二元变量，并施加线性约束

这些不等式强制在任何完全相同的时间 $$x(i)$$ 和 $$v(i)$$ 都为零，并且只要 $$x(i)>0$$，它们还强制 $$fmin\le x(i)\le fmax$$。

此外，要对投资组合中的资产数量强制进行约束，请施加线性约束

目标和连续线性逼近

对于最初表示的问题，您需要尝试最大化目标函数。然而，Optimization Toolbox™ 中的所有求解器都执行最小化计算。因此，需要将问题表示为最小化目标的负值：

此目标函数是非线性的。MILP 求解器需要线性目标函数。有一种标准方法可以将此问题重新表示为具有线性目标和非线性约束的问题。引入松弛变量 $$z$$ 来表示二次项。

在迭代求解 MILP 逼近时，您包含新线性约束，其中每个约束都在当前点附近局部逼近非线性约束。特别是，对于 $$x=x_0+\delta$$，其中 $$x_0$$ 是常量向量且 $$\delta$$ 是变量向量，约束的一阶泰勒逼近为

用 $$x-x_0$$ 取代 $$\delta$$ 得出

对于每个中间解 $$x_k$$，您在 $$x$$ 和 $$z$$ 中引入一个新线性约束，作为上述表达式的线性部分：

其形式为 $$Ax\le b$$，其中 $$A=2x_k^{T}Q$$，对于 $$z$$ 项有 $$-1$$ 乘数，且 $$b=x_k^{T}Q{x}_k$$。

这种给问题添加新线性约束的方法称为割平面法。有关详细信息，请参阅 J. E. Kelley, Jr."The Cutting-Plane Method for Solving Convex Programs."J. Soc.Indust.Appl.Math.Vol. 8, No. 4, pp. 703-712, December, 1960.

MATLAB® 问题表示

要表达优化问题，请执行以下各项：

加载问题的数据。此数据有以向量 r 形式表示的 225 个预期回报，以及以 225×225 矩阵 Q 形式表示的回报协方差。数据与在投资组合优化问题中使用二次规划的示例中使用的数据相同。

load port5
r = mean_return;
Q = Correlation .* (stdDev_return * stdDev_return');

将资产数量设置为 N。

N = length(r);

创建问题变量、约束和目标

创建表示资产分配比例的连续变量 xvars，表示相关联的 xvars 是为零还是严格为正的二元变量 vvars，以及表示 $$z$$ 变量的 zvar（正标量）。

xvars = optimvar('xvars',N,1,'LowerBound',0,'UpperBound',1);
vvars = optimvar('vvars',N,1,'Type','integer','LowerBound',0,'UpperBound',1);
zvar = optimvar('zvar',1,'LowerBound',0);

问题中所有 2N+1 变量的下界为零。xvars 和 yvars 变量的上界为 1，zvar 没有上界。

将解中的资产数量设置为 100 和 150 之间。将此约束纳入问题的形式中，即

为此需要编写两个线性约束：

M = 150;
m = 100;
qpprob = optimproblem('ObjectiveSense','maximize');
qpprob.Constraints.mconstr = sum(vvars) <= M;
qpprob.Constraints.mconstr2 = sum(vvars) >= m;

包含半连续约束。对于每种资产类型，取资产的非零最小小数为 0.001，最大小数为 0.05。

fmin = 0.001;
fmax = 0.05;

包含不等式 $$x(i)\le fmax(i)*v(i)$$ 和 $$fmin(i)*v(i)\le x(i)$$。

qpprob.Constraints.fmaxconstr = xvars <= fmax*vvars;
qpprob.Constraints.fminconstr = fmin*vvars <= xvars;

包含投资组合为 100% 投资的约束，即 $$\sum x_i=1$$。

qpprob.Constraints.allin = sum(xvars) == 1;

将风险厌恶系数 $$\lambda$$ 设置为 100。

lambda = 100;

定义目标函数 $$r^{T}x-\lambda z$$，并将其包含在问题中。

qpprob.Objective = r'*xvars - lambda*zvar;

求解问题

要以迭代方式求解问题，请首先用当前约束求解问题，这些约束尚未反映任何线性化。

options = optimoptions(@intlinprog,'Display','off'); % Suppress iterative display
[xLinInt,fval,exitFlagInt,output] = solve(qpprob,'options',options);

为迭代准备停止条件：当松弛变量 $$z$$ 在真实二次值的 0.01% 以内时停止。

thediff = 1e-4;
iter = 1; % iteration counter
assets = xLinInt.xvars;
truequadratic = assets'*Q*assets;
zslack = xLinInt.zvar;

保留计算出的真实二次变量和松弛变量的历史记录，以便绘图。设置比默认值更严格的约束容差，以帮助迭代收敛于正确的解。

history = [truequadratic,zslack];
options.ConstraintTolerance = 1e-9;

计算二次值和松弛值。如果它们不同，则添加另一个线性约束并再次求解。

每个新线性约束 $$Ax\le b$$ 来自线性逼近

找到新解后，在新解和旧解的中间使用线性约束。这种包含线性约束的启发式方法可能比直接采用新解更快。要使用解而不是半启发式方法，请对下面的“Midway”行进行注释，并取消注释其后的一行。

while abs((zslack - truequadratic)/truequadratic) > thediff % relative error
    constr = 2*assets'*Q*xvars - zvar <= assets'*Q*assets;
    newname = ['iteration',num2str(iter)];
    qpprob.Constraints.(newname) = constr;
    % Solve the problem with the new constraints
    [xLinInt,fval,exitFlagInt,output] = solve(qpprob,'options',options);
    assets = (assets+xLinInt.xvars)/2; % Midway from the previous to the current
%     assets = xLinInt(xvars); % Use the previous line or this one
    truequadratic = xLinInt.xvars'*Q*xLinInt.xvars;
    zslack = xLinInt.zvar;
    history = [history;truequadratic,zslack];
    iter = iter + 1;
end

检查解和收敛速度

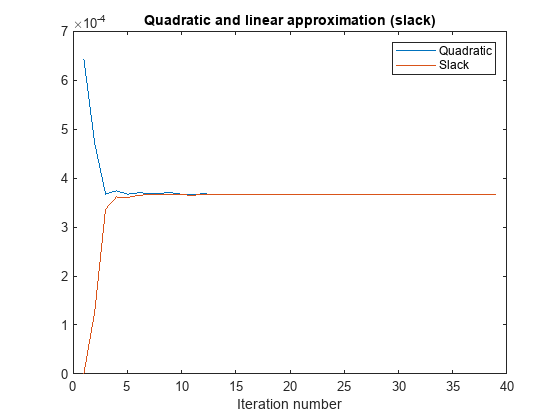
绘制松弛变量和目标函数二次部分的历史记录，看看它们是如何收敛的。

plot(history)
legend('Quadratic','Slack')
xlabel('Iteration number')
title('Quadratic and linear approximation (slack)')

MILP 解的质量如何？output 结构体包含该信息。检查在解处目标的内部计算边界之间的绝对间隙。

disp(output.absolutegap)

     0

绝对间隙为零，表明 MILP 解准确。

对最佳分配绘图。使用 xLinInt.xvars 而不是 assets，因为 assets 在使用中间的更新时可能不满足约束。

bar(xLinInt.xvars)
grid on
xlabel('Asset index')
ylabel('Proportion of investment')
title('Optimal asset allocation')

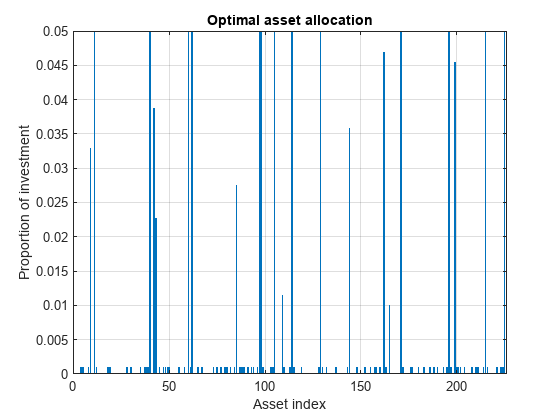
很容易看出，所有非零资产分配都在半连续边界 $$fmin=0.001$$ 和 $$fmax=0.05$$ 之间。

有多少非零资产？约束是非零资产数在 100 和 150 之间。

sum(xLinInt.vvars)

ans = 100

这种分配的预期回报是多少，风险调整后的回报值是多少？

fprintf('The expected return is %g, and the risk-adjusted return is %g.\n',...
    r'*xLinInt.xvars,fval)

The expected return is 0.000595107, and the risk-adjusted return is -0.0360382.

通过使用 Financial Toolbox® 中专为投资组合优化而设计的功能，可以进行更详细的分析。有关说明如何使用 Portfolio 类直接处理半连续和基数约束的示例，请参阅 Portfolio Optimization with Semicontinuous and Cardinality Constraints (Financial Toolbox)。