发电机的最佳调度:基于问题
此示例说明如何以最佳方式调度两台燃气发电机,即收益减去成本的值最大。虽然此示例并不完全切合实际,但它能够说明如何考虑取决于决策时机的成本。
要了解如何通过基于求解器的方法处理此问题,请参阅发电机的最佳调度:基于求解器。
问题定义
电力市场在一天的不同时段有不同用电价格。如果您使用发电机供电,您可以根据这种可变价格,安排您的发电机在用电价格高时运行。假设您控制两台发电机。每台发电机有三个功率水平(关、低和高)。每台发电机在每个功率水平下都有指定的燃料消耗率和发电量。发电机关闭时,燃料消耗为 0。
您可以为每台发电机在一天中的每个半小时区间(24 小时分为 48 个区间)分配一个功率水平。根据历史记录,假设您知道在每个时间区间内每兆瓦时 (MWh) 的收入。此示例的数据来自澳大利亚能源市场运营商 https://www.nemweb.com.au/REPORTS/CURRENT/ 2013 年中报告,数据的使用遵守其条款 https://www.aemo.com.au/privacy-and-legal-notices/copyright-permissions。
load dispatchPrice; % Get poolPrice, which is the revenue per MWh bar(poolPrice,.5) xlim([.5,48.5]) xlabel('Price per MWh at each period')

发电机关闭后启动是有成本的。此外,一天的最大燃料使用量也存在约束。此约束之所以存在,是因为您需要提前一天购买燃料,因此您只能使用刚刚购买的燃料。
问题表示和参数
您可以将调度问题表示为二元整数规划问题。定义索引 i、j 和 k,以及二元调度向量 y,如下所示:
nPeriods= 时间段数,本例中为 48。i= 一个时间段,1 <=i<= 48。对于此示例,
j= 发电机索引,1 <=j<= 2。在时间段
i中,发电机j在功率水平k上运行,表示为y(i,j,k) = 1。让低功率为k = 1,高功率为k = 2。当sum_k y(i,j,k) = 0时,发电机关闭。
确定发电机关闭后何时启动。为此,请定义辅助二元变量 z(i,j),该变量指示在时间段 i 中是否加电以启动发电机 j。
发电机
j在时间段i关闭,但在时间段i + 1打开,表示为z(i,j) = 1。在其他时间段z(i,j) = 0。换句话说,当sum_k y(i,j,k) = 0时z(i,j) = 1,且sum_k y(i+1,j,k) = 1。
您需要一种基于 y 的设置自动设置 z 的方法。以下线性约束可处理此设置。
您还需要成本问题的参数、每台发电机的发电水平、发电机的燃料消耗水平和可用燃料。
poolPrice(i)-i区间内每兆瓦时的收入(以美元为单位)gen(j,k)- 发电机j在功率水平k时产生的兆瓦数fuel(j,k)- 发电机j在功率水平k时使用的燃料totalFuel- 一天内可用的燃料startCost- 发电机关闭后启动的成本(以美元为单位)fuelPrice- 单位燃料的成本
当您执行 load dispatchPrice; 时,您得到 poolPrice。按如下所示设置其他参数。
fuelPrice = 3; totalFuel = 3.95e4; nPeriods = length(poolPrice); % 48 periods nGens = 2; % Two generators gen = [61,152;50,150]; % Generator 1 low = 61 MW, high = 152 MW fuel = [427,806;325,765]; % Fuel consumption for generator 2 is low = 325, high = 765 startCost = 1e4; % Cost to start a generator after it has been off
发电机效率
检查两台发电机在两个工作点的效率。
efficiency = gen./fuel; % Calculate electricity per unit fuel use rr = efficiency'; % for plotting h = bar(rr); h(1).FaceColor = 'g'; h(2).FaceColor = 'c'; legend(h,'Generator 1','Generator 2','Location','NorthEastOutside') ax = gca; ax.XTick = [1,2]; ax.XTickLabel = {'Low','High'}; ylim([.1,.2]) ylabel('Efficiency')
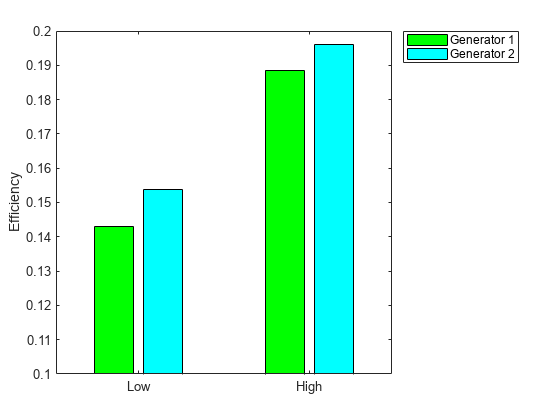
请注意,在对应的工作点(低和高)上,发电机 2 的效率稍高于发电机 1,但发电机 1 在其高工作点的效率高于发电机 2 在其低工作点的效率。
解的变量
要设置问题,您需要以问题形式对所有问题数据和约束进行编码。变量 y(i,j,k) 表示问题的解,辅助变量 z(i,j) 指示是否加电以启动发电机。y 是 nPeriods-by-nGens-by-2 数组,z 是 nPeriods-by-nGens 数组。所有变量均为二元变量。
y = optimvar('y',nPeriods,nGens,{'Low','High'},'Type','integer','LowerBound',0,... 'UpperBound',1); z = optimvar('z',nPeriods,nGens,'Type','integer','LowerBound',0,... 'UpperBound',1);
线性约束
要确保功率水平最多只有一个等于 1 的分量,可设置线性不等式约束。
powercons = y(:,:,'Low') + y(:,:,'High') <= 1;
每个时间段的运行成本就是该时间段的燃料成本。对于在 k 水平上运行的发电机 j,成本为 fuelPrice * fuel(j,k)。
创建表达式 fuelUsed 以说明使用的所有燃料。
yFuel = zeros(nPeriods,nGens,2); yFuel(:,1,1) = fuel(1,1); % Fuel use of generator 1 in low setting yFuel(:,1,2) = fuel(1,2); % Fuel use of generator 1 in high setting yFuel(:,2,1) = fuel(2,1); % Fuel use of generator 2 in low setting yFuel(:,2,2) = fuel(2,2); % Fuel use of generator 2 in high setting fuelUsed = sum(sum(sum(y.*yFuel)));
约束是所用燃料不得超过可用燃料。
fuelcons = fuelUsed <= totalFuel;
设置发电机启动指示变量
如何让求解器自动设置 z 变量以匹配 y 变量的活动/关闭时间段?前面提到过,要满足的条件是当 sum_k y(i,j,k) = 0 且 sum_k y(i+1,j,k) = 1 时,z(i,j) = 1。
请注意,当您需要 z(i,j) = 1 时,sum_k ( - y(i,j,k) + y(i+1,j,k) ) > 0。
因此,请在问题表示中包含这些线性不等式约束。
sum_k ( - y(i,j,k) + y(i+1,j,k) ) - z(i,j) < = 0.
此外,将 z 变量加入目标函数成本中。使用目标函数中的 z 变量,求解器尝试降低其值,这意味着它尝试将它们都设置为 0。但是,对于发电机开启的那些时间区间,线性不等式强制 z(i,j) 等于 1。
创建表示 y(i+1,j,k) - y(i,j,k) 的辅助变量 w。用 w 表示发电机启动不等式。
w = optimexpr(nPeriods,nGens); % Allocate w idx = 1:(nPeriods-1); w(idx,:) = y(idx+1,:,'Low') - y(idx,:,'Low') + y(idx+1,:,'High') - y(idx,:,'High'); w(nPeriods,:) = y(1,:,'Low') - y(nPeriods,:,'Low') + y(1,:,'High') - y(nPeriods,:,'High'); switchcons = w - z <= 0;
定义目标
目标函数包括运行发电机的燃料成本、运行发电机的收入和启动发电机的成本。
generatorlevel = zeros(size(yFuel));
generatorlevel(:,1,1) = gen(1,1); % Fill in the levels
generatorlevel(:,1,2) = gen(1,2);
generatorlevel(:,2,1) = gen(2,1);
generatorlevel(:,2,2) = gen(2,2); 收入 = y.*generatorlevel.*poolPrice。
revenue = optimexpr(size(y)); for ii = 1:nPeriods revenue(ii,:,:) = poolPrice(ii)*y(ii,:,:).*generatorlevel(ii,:,:); end
总燃料成本 = fuelUsed*fuelPrice。
fuelCost = fuelUsed*fuelPrice;
发电机启动成本 = z*startCost。
startingCost = z*startCost;
利润 = 收入 - 总燃料成本 - 启动成本。
profit = sum(sum(sum(revenue))) - fuelCost - sum(sum(startingCost));
求解问题
创建一个优化问题并加入目标和约束。
dispatch = optimproblem('ObjectiveSense','maximize'); dispatch.Objective = profit; dispatch.Constraints.switchcons = switchcons; dispatch.Constraints.fuelcons = fuelcons; dispatch.Constraints.powercons = powercons;
为了节省空间,请隐藏迭代输出。
options = optimoptions('intlinprog','Display','final');
求解。
[dispatchsol,fval,exitflag,output] = solve(dispatch,'options',options);Solving problem using intlinprog. Optimal solution found. Intlinprog stopped because the objective value is within a gap tolerance of the optimal value, options.RelativeGapTolerance = 0.0001. The intcon variables are integer within tolerance, options.ConstraintTolerance = 1e-06.
检查解
将解绘制为时间的函数。
subplot(3,1,1) bar(dispatchsol.y(:,1,1)*gen(1,1)+dispatchsol.y(:,1,2)*gen(1,2),.5,'g') xlim([.5,48.5]) ylabel('MWh') title('Generator 1 Optimal Schedule','FontWeight','bold') subplot(3,1,2) bar(dispatchsol.y(:,2,1)*gen(2,1)+dispatchsol.y(:,2,2)*gen(2,2),.5,'c') title('Generator 2 Optimal Schedule','FontWeight','bold') xlim([.5,48.5]) ylabel('MWh') subplot(3,1,3) bar(poolPrice,.5) xlim([.5,48.5]) title('Energy Price','FontWeight','bold') xlabel('Period') ylabel('$ / MWh')
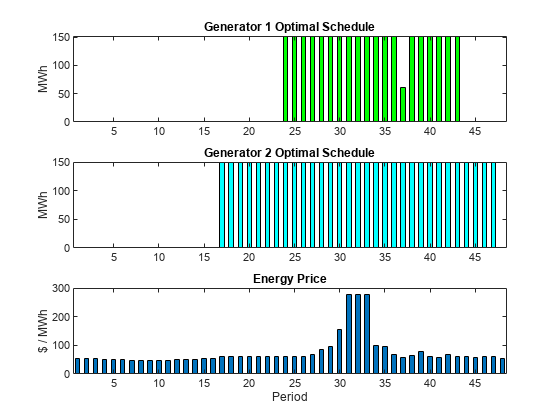
发电机 2 比发电机 1 运行时间长,这是您所期望的结果,因为这样效率更高。发电机 2 只要处于运行状态就以其高功率水平运行。发电机 1 主要在其高功率水平下运行,但在一个时间单位内降至低功率。每个发电机每天运行一组连续的时间段,因此每天只发生一次启动成本。
检查在发电机启动的时间段内 z 变量是否为 1。
starttimes = find(round(dispatchsol.z) == 1); % Use round for noninteger results
[theperiod,thegenerator] = ind2sub(size(dispatchsol.z),starttimes)theperiod = 2×1
23
16
thegenerator = 2×1
1
2
发电机启动的时间段与绘图相匹配。
与启动罚分较低的情况进行比较
如果您为 startCost 指定较低的值,则解将涉及多个发电时间段。
startCost = 500; % Choose a lower penalty for starting the generators startingCost = z*startCost; profit = sum(sum(sum(revenue))) - fuelCost - sum(sum(startingCost)); dispatch.Objective = profit; [dispatchsolnew,fvalnew,exitflagnew,outputnew] = solve(dispatch,'options',options);
Solving problem using intlinprog. Optimal solution found. Intlinprog stopped because the objective value is within a gap tolerance of the optimal value, options.RelativeGapTolerance = 0.0001. The intcon variables are integer within tolerance, options.ConstraintTolerance = 1e-06.
subplot(3,1,1) bar(dispatchsolnew.y(:,1,1)*gen(1,1)+dispatchsolnew.y(:,1,2)*gen(1,2),.5,'g') xlim([.5,48.5]) ylabel('MWh') title('Generator 1 Optimal Schedule','FontWeight','bold') subplot(3,1,2) bar(dispatchsolnew.y(:,2,1)*gen(2,1)+dispatchsolnew.y(:,2,2)*gen(2,2),.5,'c') title('Generator 2 Optimal Schedule','FontWeight','bold') xlim([.5,48.5]) ylabel('MWh') subplot(3,1,3) bar(poolPrice,.5) xlim([.5,48.5]) title('Energy Price','FontWeight','bold') xlabel('Period') ylabel('$ / MWh')
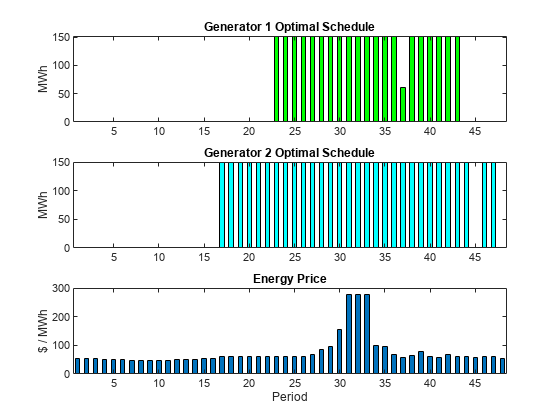
starttimes = find(round(dispatchsolnew.z) == 1); % Use round for noninteger results
[theperiod,thegenerator] = ind2sub(size(dispatchsolnew.z),starttimes)theperiod = 3×1
22
16
45
thegenerator = 3×1
1
2
2